一般枚举问题的思路很明显就能看出来要用枚举，但是难点就在于要怎么缩小每个变量的范围，一般变量之间都是有某些关系的，通过缩小枚举的范围，设置枚举的顺序，来提高枚举顺序.否则就会超时。

枚举的思路:
先想一下能把答案全部枚举到的方法，保证不重不漏，枚举所有的顺序
然后进行优化:对代码进行等价变形，有没有什么性质，利用性质来优化某些步骤

1.完美立方 百炼2810

这个一看第一反应就是暴力

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int a=2;a<=n;++a)
        for(int b=a;b<=n;++b)
            for(int c=b;c<=n;++c)
                for(int d=c;d<=n;++d)
                    if(pow(a,3)==pow(b,3)+pow(c,3)+pow(d,3))
                        cout<<"Cube = "<<a<<", Triple = ("<<b<<","<<c<<","<<d<<")"<<endl; 

    return 0;
 } 

但是运行后是这样的:

看了一圈没找出来毛病，又看了看题干,发现题干a,b,c,d大于1，那么b应该也从2开始；

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int a=2;a<=n;++a)
        for(int b=2;b<=n;++b)
            for(int c=b;c<=n;++c)
                for(int d=c;d<=n;++d)
                    if(pow(a,3)==pow(b,3)+pow(c,3)+pow(d,3))
                        cout<<"Cube = "<<a<<", Triple = ("<<b<<","<<c<<","<<d<<")"<<endl; 

    return 0;
 } 

这次输入24，输出的和样例一样，提交后显示超时.要想想怎么优化，能不能把a放在for循环的最内层呢

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int a=2;a<=n;++a)
        for(int b=a;b<=n;++b)
            for(int c=b;c<=n;++c)
                for(int d=c;d<=n;++d)
                    if(pow(a,3)==pow(b,3)+pow(c,3)+pow(d,3))
                        cout<<"Cube = "<<a<<", Triple = ("<<b<<","<<c<<","<<d<<")"<<endl; 

    return 0;
 } 

但是输出的和样例不一样

发现这样输出并不是按照题干要求的，所以还是要把a放在第一重循环，那么就要想想怎么缩小范围了.
通过看样例，发现其实b,c,d的值没必要到n，每次到n-1结束就行，所以b[2,a-1];c[b,a-1];d[c,a-1];

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int a=2;a<=n;++a)
        for(int b=2;b<a;++b)
            for(int c=b+1;c<a;++c)
                for(int d=c+1;d<a;++d)
                    if(pow(a,3)==pow(b,3)+pow(c,3)+pow(d,3))
                        cout<<"Cube = "<<a<<", Triple = ("<<b<<","<<c<<","<<d<<")"<<endl; 

    return 0;
}

但是提交后还是显示超时，想了想爱还是不知道该怎么缩了，于是看了郭炜老师的讲解发现了问题，原来是死在了pow函数上:

#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int n;
    cin>>n;
    for(int a=2;a<=n;++a)
        for(int b=2;b<a;++b)
            for(int c=b;c<a;++c)
                for(int d=c;d<a;++d)
                    if(a*a*a==b*b*b+c*c*c+d*d*d)
                        cout<<"Cube = "<<a<<", Triple = ("<<b<<","<<c<<","<<d<<")"<<endl; 

    return 0;
} 

pow的运行时间是3173ms,后边则是43ms，真是没想到哇！！！！amazing

2.数的分解 蓝桥杯2019初赛

这个题一看明显就是暴力吗，于是乎:

#include<iostream>
using namespace std;
int check(int n)
{
    while(n)
    {
        if(n%10==2||n%10==4) return 0;
        n=n/10;
    }
    return 1;
}
int main()
{
    int cnt=0;
    for(int i=1;i<2019;++i)
        for(int j=i+1;j<2019;++j)
            for(int k=j+1;k<2019;++k)
                if(check(i)&&check(j)&&check(k)&&i+j+k==2019){
                    cout<<i<<" "<<j<<" "<<k<<endl;  
                    cnt++;
                }


    cout<<cnt;
    return 0;
 }

当时在Dev跑的时候，就看着跑不出来了，算了下时间，46.7S才出结果…
那么就要优化了:

#include<iostream>
using namespace std;
int check(int n)
{
    while(n)
    {
        if(n%10==2||n%10==4) return 0;
        n=n/10;
    }
    return 1;
}
int main()
{
    int cnt=0;
    for(int i=1;i<2019;++i)
        if(check(i))
            for(int j=i+1;j<2019;++j)
                if(check(j))
                    for(int k=j+1;k<2019;++k)
                        if(check(k)&&i+j+k==2019) cnt++;
    cout<<cnt;
    return 0;
 } 

这个比上边那个要快不少，但是还是超时，还要继续优化:

#include<iostream>
using namespace std;
int check(int n)
{
    while(n)
    {
        if(n%10==2||n%10==4) return 0;
        n=n/10;
    }
    return 1;
}
int main()
{
    int cnt=0;
    for(int i=1;i<2019;++i)
        if(check(i))
            for(int j=i+1;j<2019;++j)
                if(check(j))
                {
                    int k=2019-i-j;
                    if(check(k)&&k>j) cnt++;
                }
    cout<<cnt;
    return 0;
 } 

其实最后这个优化之前看到过，多个for循环时最后一个循环用已知条件来表示.
最后想想为什么第一次看到2019后还会用三个for循环，当时也想了，时间复杂度是8*10的8次方,但是忽略了check()函数…

3.AcWing 1236. 递增三元组(第九届蓝桥杯省赛C++B组)

读完题第一反应就是暴力，没细想数据范围

#include<iostream>
using namespace std;
const int N = 100010;
int main()
{
    int n;
    int a[N],b[N],c[N];
    cin>>n;
    for(int i=0;i<n;++i) cin>>a[i];
    for(int i=0;i<n;++i) cin>>b[i];
    for(int i=0;i<n;++i) cin>>c[i];

    long long cnt=0;
    //cout<<cnt<<endl;
    for(int i=0;i<n;++i)
        for(int j=0;j<n;++j){
            if(a[i]<b[j])
                for(int k=0;k<n;++k)
                    if(a[i]<b[j]&&b[j]<c[k]) cnt++;

        }                
    cout<<cnt;
    return 0;
}

果不其然，TLE了，只通过了6/12个数据
下面就在想怎么优化:首先对每个数组进行从小到大排序，排完序以后，对于遍历a数组时，如果a[i]>b[n-1],那么对于这个i肯定没有满足的情况，对于遍历b数组时，如果b[j]>k[n-1],那么对于这个j肯定没有满足的情况.

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100010;
int main()
{
    int n;
    int a[N],b[N],c[N];
    cin>>n;
    for(int i=0;i<n;++i) cin>>a[i];
    for(int i=0;i<n;++i) cin>>b[i];
    for(int i=0;i<n;++i) cin>>c[i];

    sort(a,a+n); sort(b,b+n); sort(c,c+n);

    long long cnt=0;
    int i,j,k;
    for(i=0;i<n;++i)
        if(a[i]<b[n-1])//如果第一行的某一元素大于第二行最后一个元素(排序后最后一个元素也是最大元素)，那肯定不满足
            for(j=0;j<n;++j)
                if(a[i]<b[j])
                    for(k=0;k<n;++k)
                        if(b[j]>c[n-1]) break;
                        else{
                            if(a[i]<b[j]&&b[j]<c[k]) cnt++;
                        }
    cout<<cnt;
    return 0;
}

依旧TLE，还是只通过了6/12个数据，说明压根就不能用这三重for循环.
于是看了y总的思路:

下面先说一下前缀和的代码:

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int a[N],b[N],c[N];
int as[N];//as[i]表示在a[]中有多少个数小于b[i]
int cs[N];//cs[i]表示在c[]中有多少个数大于b[i]
int cnt[N],s[N];

long long sum=0;

int main()
{
    cin>>n;
    for(int i=0;i<n;++i) cin>>a[i],a[i]++;
    for(int i=0;i<n;++i) cin>>b[i],b[i]++;
    for(int i=0;i<n;++i) cin>>c[i],c[i]++;

    //求as[]
    for(int i=0;i<n;++i) cnt[a[i]]++;
    for(int i=1;i<N;++i) s[i]=s[i-1]+cnt[i]; //求cnt[]的前缀和
    for(int i=0;i<n;++i) as[i]=s[b[i]-1]; //因为要求的是小于，所以这个地方要-1

    //求cs[]
    memset(cnt,0,sizeof cnt);
    memset(s,0,sizeof s);
    for(int i=0;i<n;++i) cnt[c[i]]++;
    for(int i=1;i<N;++i) s[i]=s[i-1]+cnt[i];
    for(int i=0;i<n;++i) cs[i]=s[N-1]-s[b[i]];

    LL res = 0;
    //枚举每个b[i];
    for(int i = 0;i<n;++i) res+=(LL)as[i]*cs[i];

    cout<<res;

    return 0;
}

刚开始没想明白输入的时候为什么要+1，其实是把之前的0放到1的位置上了，在求前缀和的时候不用在for前写一句s[0]=cnt[0],如果不+1，那么代码如下:

#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>

using namespace std;

typedef long long LL;

const int N = 100010;

int n;
int a[N],b[N],c[N];
int as[N];//as[i]表示在a[]中有多少个数小于b[i]
int cs[N];//cs[i]表示在c[]中有多少个数大于b[i]
int cnt[N],s[N];

long long sum=0;

int main()
{
    cin>>n;
    for(int i=0;i<n;++i) cin>>a[i];
    for(int i=0;i<n;++i) cin>>b[i];
    for(int i=0;i<n;++i) cin>>c[i];

    //求as[]
    for(int i=0;i<n;++i) cnt[a[i]]++;
    s[0]=cnt[0];
    for(int i=1;i<N;++i) s[i]=s[i-1]+cnt[i]; //求cnt[]的前缀和
    for(int i=0;i<n;++i) as[i]=s[b[i]-1]; //因为要求的是小于，所以这个地方要-1

    //求cs[]
    memset(cnt,0,sizeof cnt);
    memset(s,0,sizeof s);
    for(int i=0;i<n;++i) cnt[c[i]]++;
    s[0]=cnt[0];
    for(int i=1;i<N;++i) s[i]=s[i-1]+cnt[i];
    for(int i=0;i<n;++i) cs[i]=s[N-1]-s[b[i]];

    LL res = 0;
    //枚举每个b[i];
    for(int i = 0;i<n;++i) res+=(LL)as[i]*cs[i];

    cout<<res;

    return 0;
}

4.百炼3237

这个题不是第一次做，是第二次， 第一次的题解在这. 下面来看一下这次第一反应的代码:

#include<iostream>
using namespace std;
int main()
{
    int n,a,max=0,min=0;
    cin>>n;
    while(n--)
    {
        cin>>a;
        if(a%2!=0) cout<<"0 0"<<endl;
        else
            cout<<a/4+(a%4)/2<<" "<<a/2<<endl;
    }

}

这个思路还是之前的那个思路，但是代码更加的精简了.读完这个题后脑海中就蹦出来要想最少就要兔子尽量的多，要想最多就要让鸡最多，然后又蹦出来当a为奇数时肯定要输出0 0，偶数时肯定有答案.做过的题总会发挥作用的哈哈哈.

5.AcWing 422. 校门外的树

思路:

读完题后，在看了看数据范围也不大，就有了思路————暴力
先将整个区间范围初始化为false，然后遍历每个输入的数组。对于每个输入的数组范围里边的树进行true。遍历完以后就统计整个数组中false的数量:

#include<iostream>
using namespace std;
int a[10005];//默认为false,表示没有被砍掉
int main()
{
    int l,m,sum=0;
    cin>>l>>m;
    while(m--)
    {
        int fir,las;
        cin>>fir>>las;
        for(int i=fir;i<=las;++i)
            a[i]=true;//表示被砍掉
    }
    for(int i=0;i<=l;++i)
        if(!a[i])
            sum++;
    cout<<sum;
    return 0;
}

这样提交后能AC。上面思路的时间复杂度为O(n*m).由于上面的数据范围不大所以能AC.

优化:

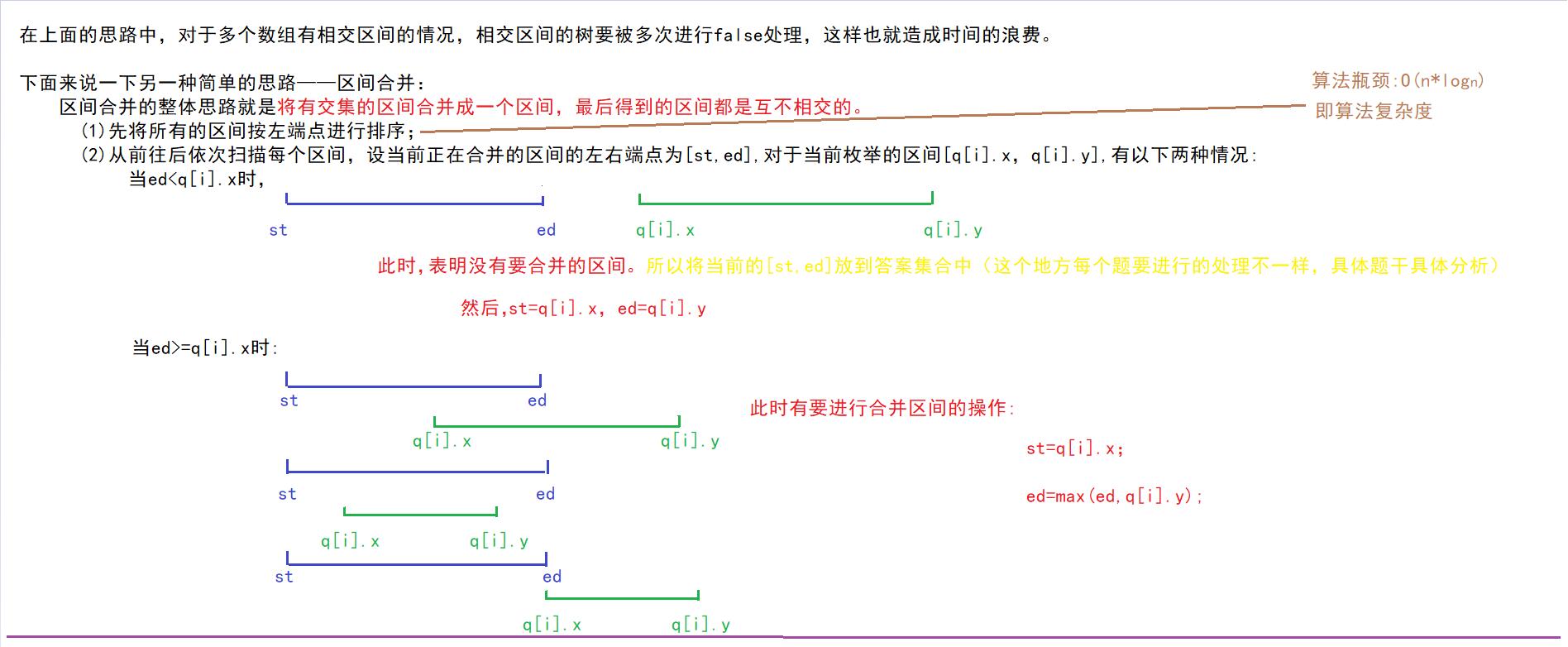
下面来看一下算法实现:

#include<cstring>
#include<iostream>
#include<algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 110;

int n,m;
PII q[N];

int main()
{
    cin>>n>>m;
    for(int i=0;i<m;++i) cin>>q[i].x>>q[i].y;//读入数组
    sort(q,q+m);//排序

    int sum=0;//被砍掉的树的数量
    int st=0,ed=-1;//正在合并区间的左右端点:
    for(int i=0;i<m;++i)//遍历所有区间
        if(ed<q[i].x)
        {
            sum += ed-st+1;//记得要加1
            st=q[i].x,ed=q[i].y;
        }
        else ed=max(ed,q[i].y);

    sum += ed-st+1;//最后一个区间也要计数，容易忘！！！！

    cout << n+1-sum <<endl;
    return 0;
}