首先总体思想如图所示

先说结论 有权边树再求直径的过程中不用向上求一段最大路径，只用求自己作为最高点所拥有的最大值d1和次大值d2，但是如果是无权边就要向上再求一段最大路径

个人感觉求不求向上的最大路径主要还是因为有权和无权树中求直径是因为一个使求边数最大一个是在求边长之和最大

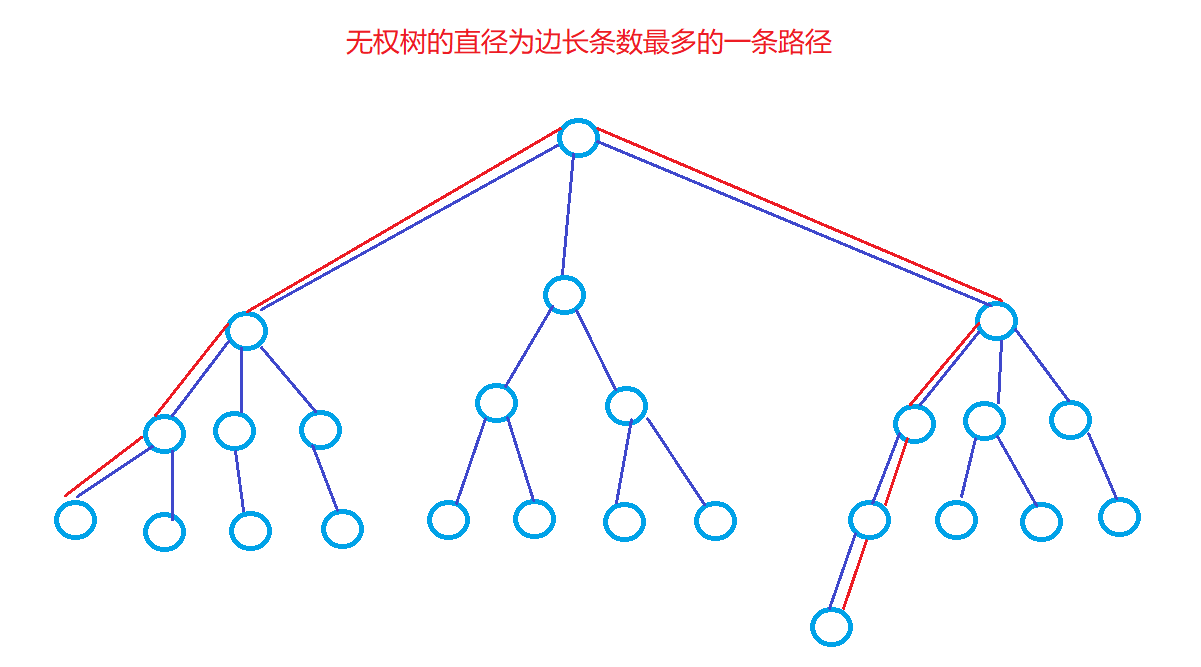
无权树求最大直径典型例题AcWing 1078. 旅游规划

AcWing 1078. 复杂DP-习题 旅游规划(树型DP)

分析

本题实际上让我们找到树的所有直径上的节点。

思路：首先就是需要确定树的最大直径，然后就是找到所有最大直径路径上的点。

那么如何确定在直径路径上的点呢？

• 计算得到一个结点向下的一条最大路径(包含次大的)及向上的最大路径。
• 最终遍历一遍所有节点，拿到该结点下方的最大值+上方的最大值，若是相加的值为树的直径，那么表示该节点属于最大直径上的点。

总体思路图示

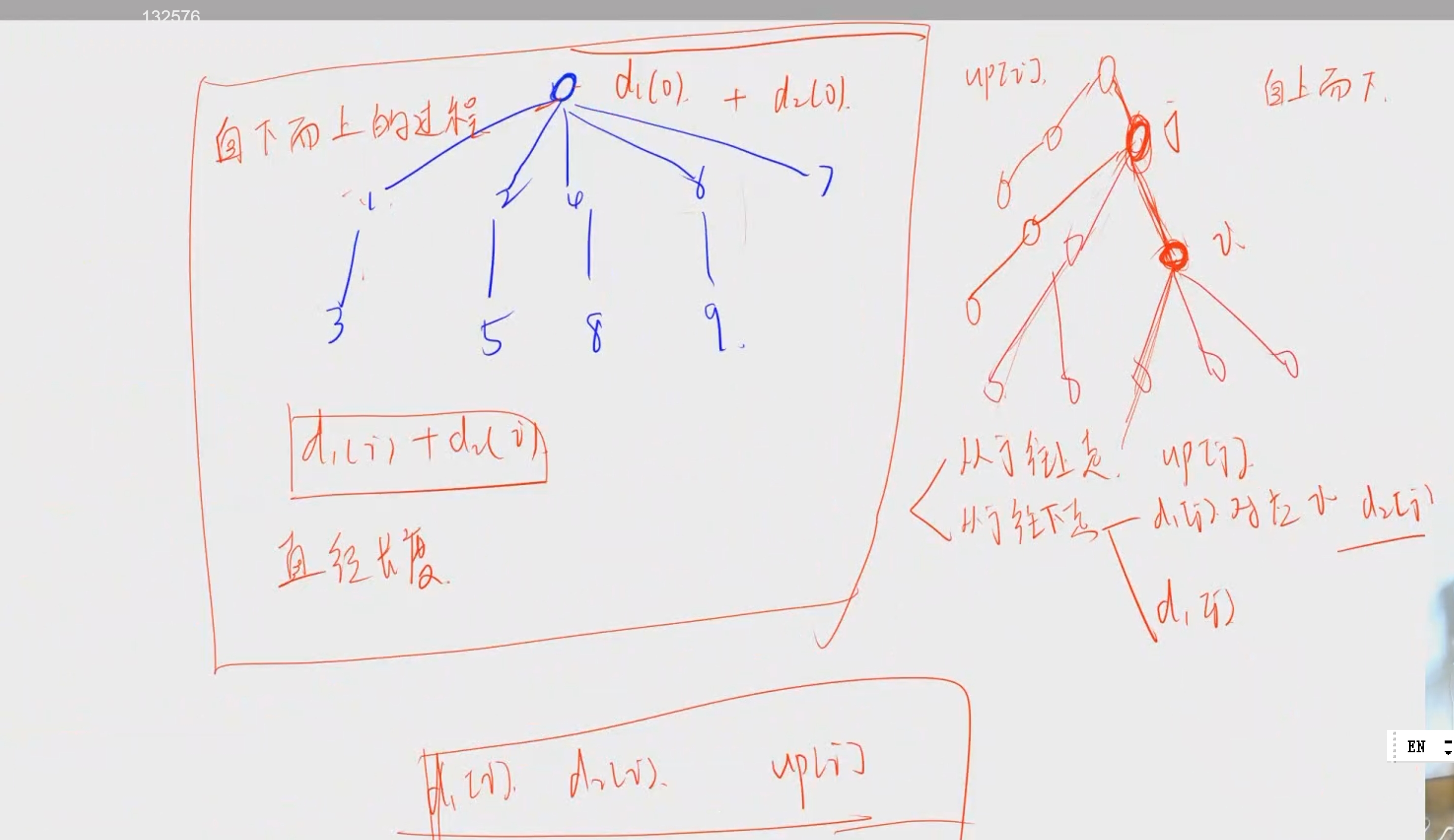
对于代码中的搜索节点下方最大距离和节点上方的最大距离有几个点来进行图示说明：

①节点之下：对于确定某个节点自下而上的最大距离和次大距离，记录长度从最底部开始向上延伸

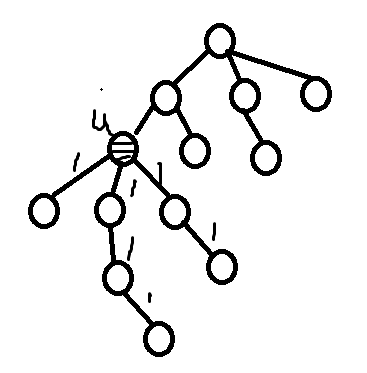
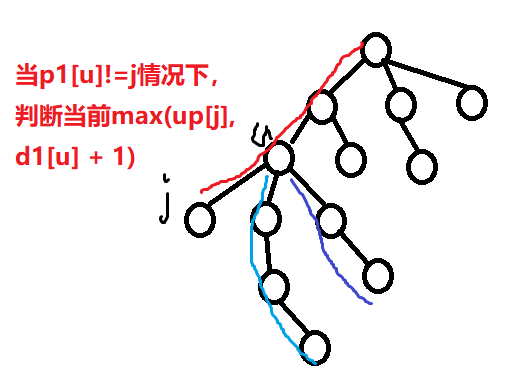
②节点之上：对于看某个点的向上的最大路径，两种情况如下所示

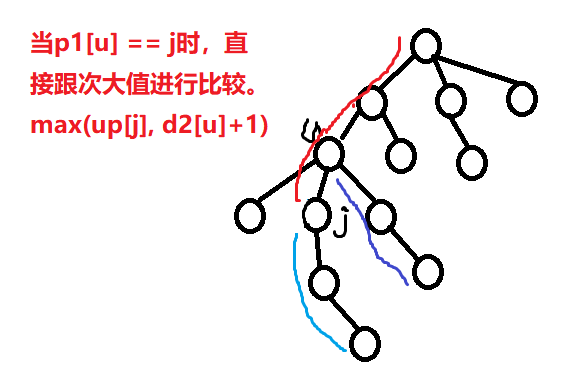
分析总结

$$\begin{aligned}&\text{变量定义与解释:我们使用}dis1[i]\text{表示点}i\text{往下走所能走的最远距离,}dis2[i]\text{表示点}i\text{往下}\\&\text{走所能走的次远距离(非严格)},next1[i]\text{表示点}i\text{往下走的最远路径上的下一个点的编}\\&\text{号,}up[i]\text{表示点}i\text{往上走所能走的最远距离。}\end{aligned}$$

$$\begin{aligned}&\text{树的直径:即树中的最长路径。求解的的直径的其中一种方式是任选一点}x\text{,求出距离}x\text{最}\\&\text{远的点}y,\text{然后再以}y\text{为起点求出距离}y\text{最远的点的距离,则该距离就为树的直径,但是这种}\\&\text{解法法用于本题,本题需要求解出可能在树的直径(可能有多条直径)上的所有点。那}\\&\text{么我们换个思路,树的直径}maxd\text{就是所有节点往下走的最大距离与次大距离之和中的最}\\&\text{大值,即}maxd=max(dis1[i]+dis2[i])\text{。}\end{aligned}$$

$$\begin{aligned}&\text{变量求解:求解}dis\text{时需要用子节点}j\text{更新父节点}u\text{,即}u\text{往}j\text{这跳路径上走的最远距离就为}\\&dis1[j]+1\text{,如果该值大于}dis1[u]\text{ ,那么}dis2[u]=dis1[u],dis1[u]=dis1[j]+1,\\&\text{即次远距离先更新为最远距离然后再更新最远距离,然后记录}next1[u]=j\text{;否则如果大}\\&\text{于}dis2[u]\text{则单独更新}dis2\text{即可。求解}up\text{时需要用父节点}u\text{更新子节点}j\text{,}j\text{往上走有两种}\end{aligned}$$

$$\begin{aligned}&\text{情况,一种是走到}u\text{然后再往上走,即}up[j]=up[u]+\text{1,一种是走到}u\text{然后往下走,往}\\&\text{下走的话肯定是优先走最远的那条路,但是如果最远的那条路就是}u\to j\text{这条则不能走,}\\&\text{因此如果}next1[u]\neq j\text{,则}up[j]=dis1[u]+1\text{,否则}up[j]=dis2[u]+1\text{。}\end{aligned}$$

$$\begin{aligned}&\text{如何判断某个点}i\text{是否在直径上呢?这个点往下走有多条路径,往上走只有一条路径,也就}\\&\text{是是到父节点,那么经过这个点的所有路径中最长的那条的长度一定是}\\&dis1[i],dis2[i],up[i]\text{中较大的两者之和(因为不确定}dis2[i]\text{和}up[i]\text{谁更大因此两者都需}\\&\text{要考虑)。如果较大的两个数之和等于树的直径,那么这个点就在某条直径上。}\end{aligned}$$

题解：树型DP及树的直径

复杂度分析：时间复杂度$O(n)$；空间复杂度$O(1)$

Java版本

import java.io.*;
import java.util.*;

class Main {

    static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
    static final int N = 200010, M = N * 2;
    //邻接表存储图，单链表数组写法
    static int[] e = new int[M], ne = new int[M], h = new int[N];
    static int idx;
    //存储节点向下的最大距离d1(含最大距离的最近节点p1)及次大距离d2；节点向上的最大距离up
    static int[] d1 = new int[N], d2 = new int[N], p1 = new int[N], up = new int[N];
    //树的直径
    static int maxd;
    //输入n长度
    static int n;

    //找寻节点向下的最大距离与次大距离
    public static void dfs_down(int u, int f) {
        //遍历所有节点
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            //不重复搜索
            if (j != f) {
                //先进行递归
                dfs_down(j, u);
                //进行从上至上距离增加
                int distance = d1[j] + 1;
                //若是当前距离>最大值，更新最大值和次大值
                if (distance > d1[u]) {
                    d2[u] = d1[u];
                    d1[u] = distance;
                    p1[u] = j;
                }else if (distance > d2[u]) { //若是当前距离>次大值，更新次大值
                    d2[u] = distance;
                }
            }
        }
        maxd = Math.max(maxd, d1[u] + d2[u]);
    }

    //找寻节点向上的最大距离
    public static void dfs_up(int u, int f) {
        for (int i = h[u]; i != -1; i = ne[i]) {
            int j = e[i];
            if (j != f) {
                //从上向下开始距离增加
                up[j] = up[u] + 1;
                //若是u节点的向下的最大节点为j，那么直接去进行比较次大值及当前up[j]
                //不选择原先的向下的最大路径避免重复，此时选择次大值
                if (p1[u] == j) {
                    up[j] = Math.max(up[j], d2[u] + 1);
                }else {
                    //若当前往下并不是之前最大点，那么实际上就可以将之前节点下方的最大路径
                    up[j] = Math.max(up[j], d1[u] + 1);
                }
                dfs_up(j, u);
            }
        }
    }

    //添加到邻接表中
    public static void add (int a, int b) {
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }

    public static void main (String[] args) throws Exception{
        n = Integer.parseInt(cin.readLine());

        //初始化头部结点
        Arrays.fill(h, -1);

        for (int i = 1; i < n; i ++ ) {
            String[] ss = cin.readLine().split(" ");
            int a = Integer.parseInt(ss[0]);
            int b = Integer.parseInt(ss[1]);
            //添加到邻接表中
            add(a, b);
            add(b, a);
        }

        //向下进行搜索取得树的直径、每个节点向下的最大路径值及次大路径值
        dfs_down(0, - 1);

        //向上来进行搜索，取得每个节点的上方的最大路径
        dfs_up(0, -1);

        //遍历所有节点，找到节点上方最大路径、节点下方最大及次大路径中的两个最大长度进行相加
        //若是相加值为树的直径，那么该结点就需要显示
        //System.out.printf("maxd : %d\n", maxd);
        for (int i = 0; i < n; i ++) {
            int[] paths = {d1[i], d2[i], up[i]};
            Arrays.sort(paths, 0, 3);
            //选择最大的两个路径值合并
            if (paths[1] + paths[2] == maxd) {
                System.out.println(i);
            }
        }

    }

}

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 200010, M = N * 2;

int n;
int h[N], e[M], ne[M], idx;
int d1[N], d2[N], p1[N], up[N];
int maxd;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs_d(int u, int father)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j != father)
        {
            dfs_d(j, u);
            int distance = d1[j] + 1;
            if (distance > d1[u])
            {
                d2[u] = d1[u], d1[u] = distance;
                p1[u] = j;
            }
            else if (distance > d2[u]) d2[u] = distance;
        }
    }

    maxd = max(maxd, d1[u] + d2[u]);
}

void dfs_u(int u, int father)
{
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j != father)
        {
            up[j] = up[u] + 1;
            if (p1[u] == j) up[j] = max(up[j], d2[u] + 1);
            else up[j] = max(up[j], d1[u] + 1);
            dfs_u(j, u);
        }
    }
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    dfs_d(0, -1);
    dfs_u(0, -1);

    for (int i = 0; i < n; i ++ )
    {
        int d[3] = {d1[i], d2[i], up[i]};
        sort(d, d + 3);
        if (d[1] + d[2] == maxd) printf("%d\n", i);
    }

    return 0;
}

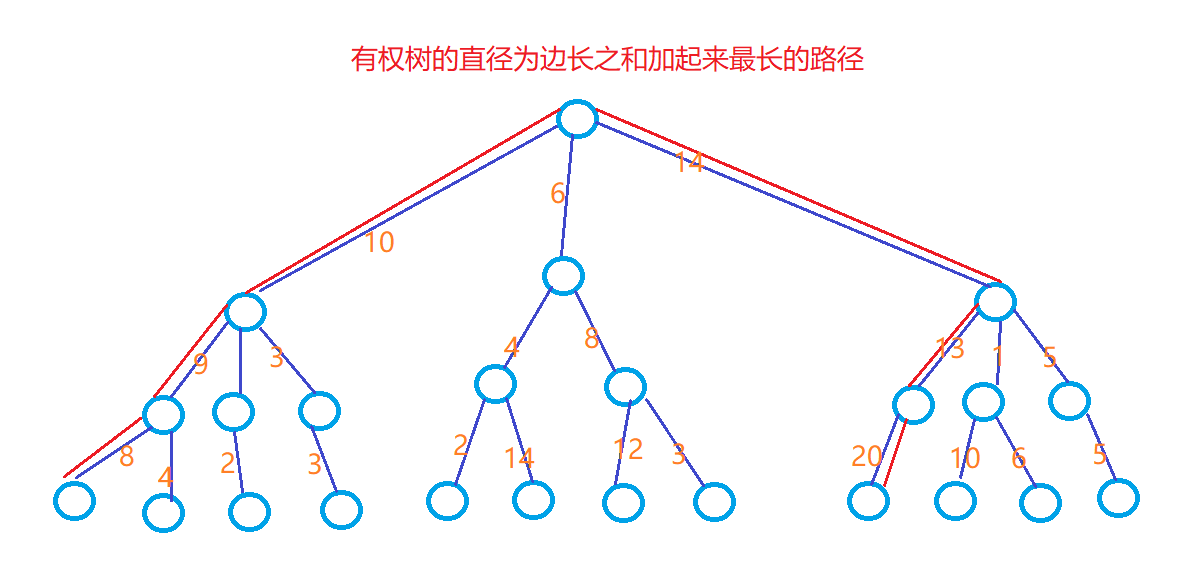
有权树就只用求d1和d2

AcWing 1072. 树的最长路径【树形DP】 - AcWing

题目描述

给定一个含有 $n$ 个节点的 树，以及树中每条边的 权值 $w_{edge_i}$

现需要在树中找出一条 路径，使得该 路径 上所有 边 的 权值之和 最大

分析

这是一道比较经典的 树形DP 题目，我们来一步步来剖析这个问题

我们知道：树上 任意两点 的路径是 唯一 确定的，因此我们可以暴力枚举 起点 和 终点 找出最长路径

如果这样做的话，我们来思考一下时间复杂度：

1. 枚举 起点 和 终点 — $O(n^2)$
2. 找出两点之间的路径长度 — $O(\log n)$

这里找出两点之间的路径有很多种做法，预处理 st 表然后倍增求LCA、树链剖分、Link-Cut Tree

但是光是枚举 起点 和 终点，时间复杂度 就直接拉满了，显然这种做法不可取

既然这 $O(n^2)$ 条路径不能 一一枚举，那么有什么方式可以把他们 分类枚举 呢？

我们考虑换一种 枚举方式：枚举路径的 起点和终点 $\rightarrow$ 枚举路径的 中间节点

我们先讨论一下，对于给定拓扑结构的树里的任意节点，经过他的路径有哪些：

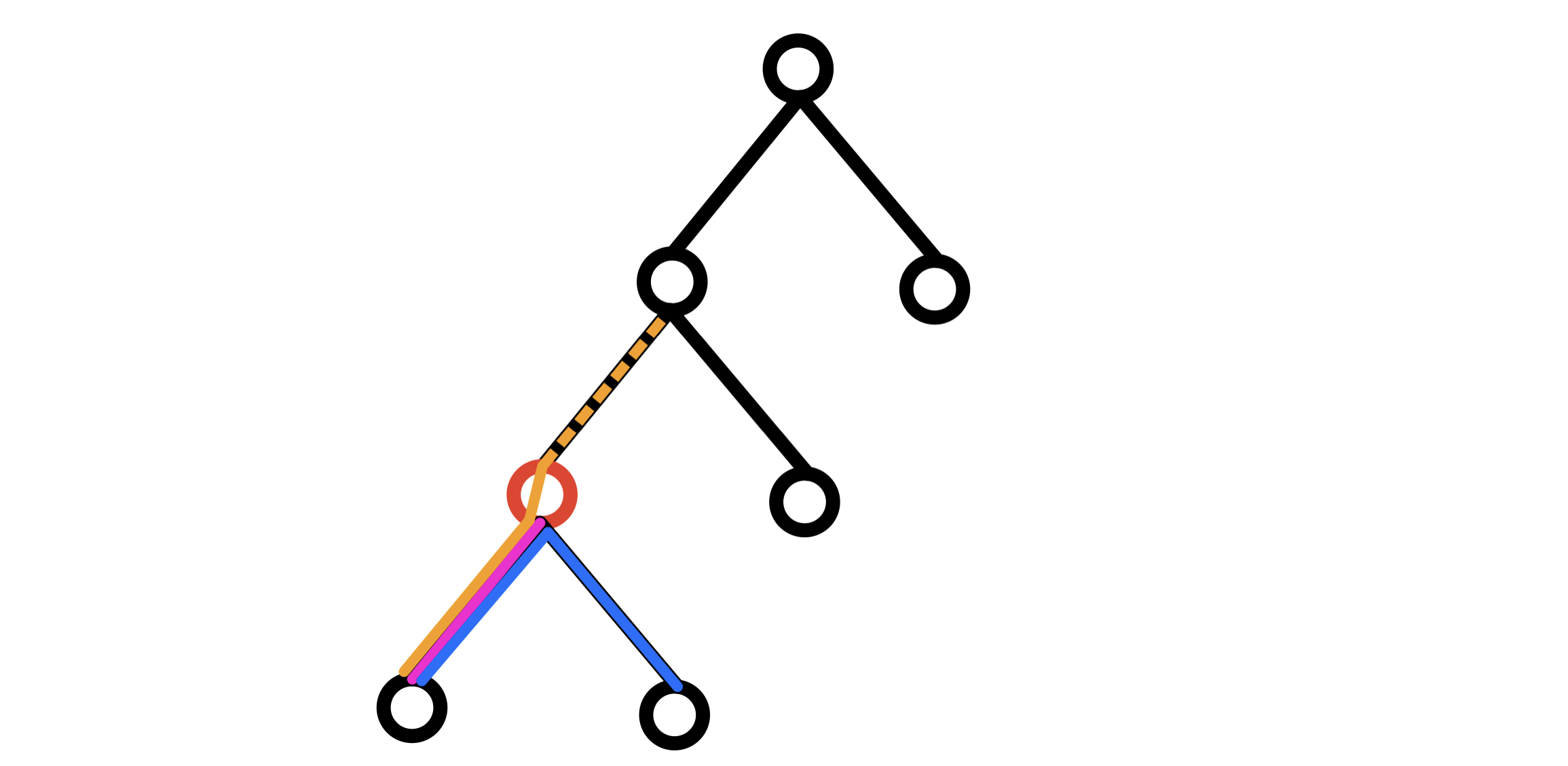
观察我标出的 红色节点，那么经过他的路径有：

1. 以其 子树中的某个节点 作为 起点，以他作为 终点 的 粉色路径
2. 以其 子树中的某个节点 作为 起点，以 子树中的某个节点 作为 终点 的 蓝色路径
3. 以其 子树中的某个节点 作为 起点，以 非其子树的节点 作为 终点 的 橙色路径

对于第 $1$ 种情况，我们可以直接递归处理其子树，找出到当前子树根节点最长的路径长度即可

对于第 $2$ 种情况，我们在处理第 $1$ 种情况时，顺便找出 $1$ 类路径的 次长路径

把 最长 和 次长 拼在一起，就是我们要的第 $2$ 种情况

而对于第 $3$ 种情况，我们可以把它归类为其 祖先节点 的第 $1,2$ 种情况，让其 祖先节点 去处理即可

把上述两类路径的分析，用 闫氏DP分析法 写出，就是如下形式：

闫氏DP分析法

状态表示—集合$f_{1/2,i}$: 以节点 $i$ 为根的子树中，从子树某个节点到 $i$ 的最长路为 $f_{1,i}$，次长路为 $f_{2,i}$
状态表示—属性$f_{1/2,i}$: 路径长度的最大值 $Max$
状态计算—$f_{1/2,i}$

$$\begin{cases} f_{1,i} = max(f_{1,i_c1} + w_{i,i_{c1}}) &c1 \in i_{child}\\ f_{2,i} = max(f_{1,i_c2} + w_{i,i_{c2}}) &c2 \in i_{child} ~\&~ c2 \ne c1 ~\&~ f_{2,i} \le f_{1,i} \end{cases}$$

Code

时间复杂度：$O(n)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1e4 + 10, M = N << 1; //初始不确定树的拓扑结构，因此要建立双向边

int n;
int h[N], e[M], w[M], ne[M], idx;
int f1[N], f2[N], res;

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dfs(int u, int father)
{
    f1[u] = f2[u] = 0;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if (j == father) continue;
        dfs(j, u);
        if (f1[j] + w[i] >= f1[u]) f2[u] = f1[u] ,f1[u] = f1[j] + w[i]; //最长路转移
        else if (f1[j] + w[i] > f2[u]) f2[u] = f1[j] + w[i];            //次长路转移
    }
    res = max(res, f1[u] + f2[u]);
}
int main()
{
    memset(h, -1, sizeof h);
    scanf("%d", &n);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }
    dfs(1, -1); //我们可以任意选取一个点作为根节点，这样整棵树的拓扑结构被唯一确定下来了
    printf("%d\n", res);
    return 0;
}

第二种方法求直径

AcWing 1207. 大臣的旅费 - AcWing

$2次dfs求树的直径$
$1. 任选一个起始节点开始dfs或bfs，直到到达距离它最远的节点maxu;$
$2.从maxu再次开始dfs或bfs，直到到达距离maxu最远距离的点p$
$3.maxu到p的路径就是树的直径$

$任何一颗树都是二分图$
$所以有以上性质$

证明过程

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>

using namespace std;
typedef long long ll;
const int N = 100010;

int n;
struct Edge
{
    int id, w;
};
vector<Edge> h[N];
int dist[N];

void dfs(int u, int father, int distance)
{
    dist[u] = distance;

    for(auto node : h[u])
        if(node.id != father)
            dfs(node.id, u, distance + node.w);
}

int main()
{
    cin >> n;
    for(int i = 0; i < n - 1; i ++)
    {
        int a, b, c;
        cin >> a >> b >> c;
        h[a].push_back({b, c});
        h[b].push_back({a, c});
    }

    dfs(1, -1, 0);

    int u = 1;
    for(int i = 1; i <= n; i ++)
        if(dist[i] > dist[u])
            u = i;

    dfs(u, -1, 0);

    for(int i = 1; i <= n; i ++)
        if(dist[i] > dist[u])
            u = i;

    int s = dist[u];

    cout << s * 10 + s * (s + 1ll) / 2;

    return 0;
}