T1
题目描述
随着互联网的发展,公司越来越重视用户体验,目标用户的统计对数据分析来说越来越重要,下面是某产品的用户信息表,表结构如下:
| 字段名 | 类型 | 备注 |
|---|---|---|
| user_id | varchar(16) | 用户id,唯一 |
| user_name | varchar(32) | 用户姓名,不保证唯一 |
请仔细阅读SQL,理解SQL输出含义,并用程序语言,模拟计算过程。
select
count(user_name) as cnt
from (
select
user_name
from
user_info a
group by user_name
having count(distinct user_id) >= 2
) b
输入描述
第一行一个整数$n$,表示表中数据的记录数,$0 \leq n \leq 1000$
接下来$n$行,每行两个字符串代表user_id和user_name,字符串之间用空格分隔,表示数据表中的一条记录,无非法记录
输出描述
结合输入数据,输出上述SQL的执行结果。
示例1
样例输入
3
10001 李华
10002 张三
10003 李四
样例输出
0
算法
(哈希表) $O(n)$
- 一个用户姓名可能会对应多个用户id
- 求对应的用户id个数大于等于2的用户姓名有多少个
- 哈希表的键为用户姓名,值是一个包含了用户id的数组
时间复杂度
插入哈希表和枚举哈希表中的每个用户姓名的时间复杂度均为$O(n)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
int n;
unordered_map<string, vector<string>> S;
string u_id, u_name;
int main() {
cin >> n;
while (n -- ) {
cin >> u_id >> u_name;
if (S.count(u_name)) S[u_name].push_back(u_id);
else S[u_name] = {u_id};
}
int cnt = 0;
for (auto name: S)
if (name.second.size() >= 2)
cnt ++ ;
cout << cnt;
return 0;
}
T2
题目描述
小木是个充满了奇思妙想的孩子,他脑子里总有各种各样天马行空的想法。有一天,他想到了这么一个问题,假设我们身处于某个迷宫之中,但我们并不知道迷宫的具体形状,只知道迷宫是由一个个格子组成,这些格子有些是可以行走的,有些是不能行走的(可能有障碍物,可能是边缘)。我们希望逃出这个迷宫,我们可以利用的只有一个$move(direction)$的函数,$direction$可以输入的参数为0,1,2,3,分别表示向上,下,左,右尝试走一格。如果操作成功,函数会返回1,并且我们就会身处在新的格子上。如果失败,则函数返回-1,我们还在原来的格子上。
假设从起点到终点(迷宫的出口)格子一定包含一条可行路径,并且我们已经得到了这个完整的利用$move$函数从起点走到终点的探索信息。小木想知道的是,假设我们从起点开始重新走一次,我们能否只利用这些已知的格子信息(未探索到的格子因为不清楚是否能走,所以以不可走处理),判断出我们从起点到迷宫出口的格子,采用最优方案的情况下,最少需要走多少步。
输入描述
输入第一行为一个正整数$T$($T \leq 10$),表示有$T$组数据。
每组数据的第一行为正整数$N$($N \leq 10 ^ 6$),后面有$N$行,每行由“$X Y$”表示,其中X($0 \leq X \leq 3$)表示$move$函数中的参数$direction$,$Y$为1或-1,表示$move$操作成功与否,1表示成功,-1表示失败。
保证最后一个操作一定是成功的操作,并且最后所处的位置就是迷宫的出口格子,并且保证是第一次来到这个出口的格子。
输出描述
对于每一组数据,输出一个正整数,表示根据整个操作信息,得到的最少的从起点到迷宫出口格子的操作步数。
示例1
样例输入
3
10
0 1
0 -1
1 1
1 1
1 -1
0 1
2 1
2 -1
3 1
3 1
2
3 1
3 1
8
0 1
0 1
3 1
3 1
1 1
1 1
2 1
0 1
样例输出
1
2
2
说明
第一个样例,根据探索的信息,我们可以知道:
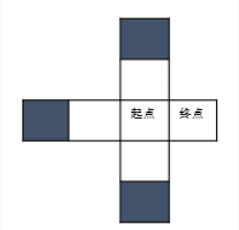
所以从起点到终点只需要1步。
第二个样例,根据探索的信息,我们可以知道:
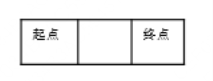
所以从起点到终点只需要2步。
第三个样例,根据探索的信息,我们可以知道:
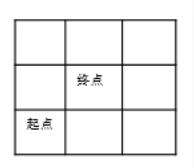
所以从起点到终点只需要2步。
算法
(BFS) $O(T \times n)$
- 开一个集合存放所有能到达的点
- 行走的偏移量需与题目说明一致
- 不走回头路,开一个状态数组保存已经走过的点
- 最开始写了一版最短路算法,那么第三个case会过不去
时间复杂度
$T$组数据,每一组最坏情况下$n$个操作能得到$n$个点,比如直线这种,时间复杂度为$O(n)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
int T, n, x, y;
struct Node {
int x, y, v;
Node(int _x, int _y, int _v) : x(_x), y(_y), v(_v) {}
};
set<PII> S;
PII d[] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
PII ed;
int main() {
cin >> T;
while (T -- ) {
S.clear();
cin >> n;
S.insert({0, 0});
x = 0, y = 0;
for (int i = 0; i < n; i ++ ) {
int a, b; cin >> a >> b;
if (b == 1) {
x += d[a].x, y += d[a].y;
S.insert({x, y});
}
if (i == n - 1) ed = {x, y};
}
queue<Node> q;
q.push({0, 0, 0});
set<PII> st;
int ret = INT_MAX;
while (q.size()) {
auto pos = q.front(); q.pop();
if (pos.x == ed.x && pos.y == ed.y) {
ret = pos.v;
break;
}
for (int i = 0; i < 4; i ++ ) {
int a = pos.x + d[i].x, b = pos.y + d[i].y;
PII ne_pos = {a, b};
if (S.find(ne_pos) != S.end() && st.find(ne_pos) == st.end()) {
q.push({a, b, pos.v + 1});
st.insert(ne_pos);
}
}
}
cout << ret << endl;
}
return 0;
}
T3
题目描述
某游戏有$N$个日常任务,玩家每日可以完成感情兴趣的任务并获取金币奖励。每个任务结束后,系统发放的金币数量均符合高斯分布,但不同任务有不同的均值和标准差。数据分析师小明从服务器获取了一批任务结算日志,准备计算出每个高斯分布的均值和标准差。但是日志生成过程中,任务名称字段发生了缺失,小明只获取了任务结束后发放的金币数量,无法分辨每次金币奖励属于哪个任务。金币数量序列如下所示:
$$4、18、36、89、87,。。。,5,90$$
于是,小明准备利用高斯混合模型来刻画数据分布,并使用$EM$(期望最大化)来求解$GMM$的各个参数。请根据以下描述和要求利用$EM$求解$GMM$。给定$GMM$:
$$ p(x | \theta) = \sum_{k} \alpha_{k}N(x|\mu_k, \sigma_k) = \sum_{k} \alpha_{k} \frac{1}{\sqrt{2\pi\sigma_{k}^2}} exp [-\frac{(x - \mu_k)^2}{2\sigma_{k}^2}] (1)$$
其中$\theta$代表全体模型参数$\alpha_k, \mu_k, \sigma_k$,$\alpha_k$为第$k$个高斯模型的先验概率,所有高斯模型的先验概率加和为1,$\mu_k, \sigma_k$分别为第$k$个高斯模型的均值和标准差。
现在有一批样本$x = \{x_1, x_2, \dots, x_n\}$,为每个样本增加一个隐变量$z_i$,表示样本$x_i$来自于哪个高斯分布,这是一个离散型随机变量,取值范围为$\{1, \dots, K\}$,令每个取值的概率为$w_{i,k}$,$x_i$的似然函数可以写成:
$$ p(x | \theta) = \sum_{k} p(z_i=k)p(x_i|z_i=k,\mu_k,\sigma_k) = \sum_{k} \alpha_{k}p(x_i|z_i=k,\mu_k,\sigma_k) (2)$$
由此可以根据贝叶斯准则推导得到其中的后验概率:
$$ w_{i,k} = p(z_i=k|x_i,\mu_k,\sigma_k) = \frac{\alpha_{k}N(x_i|\mu_k, \sigma_k)}{\sum_{k}\alpha_{k}N(x_i|\mu_k, \sigma_k)} (3)$$
进而结合$Jensen$不等式可以得到简化后的对数似然函数如下:
$$ L(x | \theta) = \sum_{i}\sum_{k}w_{i,k}\ln{\frac{\alpha_{k}N(x_i|\mu_k, \sigma_k)}{w_{i,k}}} (4)$$
有了后验概率与似然函数,就可以利用$EM$算法求解$GMM$模型中的参数了,求解过程具体如下所示:
1、输入$x$:
2、初始化参数$\theta ^ 0 = \alpha_k, \mu_k, \sigma_k$
3、循环第$t$轮:
E-Step:根据参数$\theta ^ {t - 1}$,计算后验概率$w_{i,k}^{t}$
M-Step:将$w_{i,k}^{t}$代入似然函数并对参数求导得到更新后的参数$\theta ^ {t}$,迭代时请先计算出$\mu_k$,然后利用本轮计算出的$\mu_k$来更新$\sigma_k$。
4、循环到第$T$轮结束
5、输出:$\theta ^ {T}$
由于$\alpha_k$的求导过程较为复杂,下面给出似然函数$L(x | \theta)$对$\alpha_k$求导结果:
$$ \alpha_k ^ t = \frac{\sum_{i} w_{i,k}^{t-1}}{n} (5)$$
请自行对似然函数(4)进行求导以计算$\mu_k, \sigma_k$更新公式。
请要求以上描述和式子(3)(4)(5),利用$EM$算法救解$GMM$中的参数$\theta = \alpha_k, \mu_k, \sigma_k$
注:$\pi = 3.141592658979323846264$
输入描述
第一行为三个数字K、N、M,分别表示高斯分布个数,样本个数和迭代轮数。
接下来K行分别为K个高斯分布的初始化参数,依次为高斯分布的先验概率、均值和标准差。
最后一行分别为N第一维样本数据,每一个数字对应一条样本。
输出描述
按输入的初始化参数的格式输出更新后的参数。即对于每个高斯分布,依次输出一行,分别为行验概率、均值和标准差。所有的输出数值都按照四舍五入保留5位小数。
示例1
样例输入
3 20 3
0.5 0.5 1
0.3 5.5 2
0.2 7 6
0.82 0.22 -0.03 -1.00 -0.97 5.81 -1.50 0.46 4.52 6.32 19.44 0.59 -10.05 -0.09 3.49 1.68 -1.88 1.31 7.75 2.02
样例输出
0.60810 0.12075 1.15763
0.21609 5.35956 1.63643
0.17581 4.06074 11.34718
算法
(模拟) $O(K + N + M * N * K ^ 2)$
$$ \mu_k = \frac{\sum_{i=1}^{N}w_{i,k}x_i}{\sum_{i=1}^{N}w_{i,k}} $$
$$ \sigma_k = \frac{\sum_{i=1}^{N}w_{i,k}(x_i - \mu_k) ^ 2}{\sum_{i=1}^{N}w_{i,k}} $$
时间复杂度
- 输入数据,时间复杂度为$O(K + N)$
- 训练过程,一共迭代$M$次,每次两个过程
- $E-Step$:更新$W$,时间复杂度为$O(N * K * K)$
- $M-Step$:
- 更新均值:时间复杂度为$O(K * N)$
- 更新标准差:时间复杂度为$O(K * N)$
- 更新先验概率:时间复杂度为$O(K * N)$
- 输出答案:时间复杂度为$O(K)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
const double PI = 3.1415926535;
int K, N, M;
vector<double> alpha, mu, sigma, input;
vector<vector<double>> w;
double gaussian(double x, double mu_k, double sigma_k) {
return exp(- (x - mu_k) * (x - mu_k) / (2 * sigma_k)) / sqrt(2 * PI * sigma_k);
}
void update_w(int i, int k) {
// update w_ik
w[i][k] = alpha[k] * gaussian(input[i], mu[k], sigma[k]);
double tot = 0;
for (int k = 0; k < K; k ++ )
tot += alpha[k] * gaussian(input[i], mu[k], sigma[k]);
w[i][k] /= tot;
}
double get_tot_w(int k) {
double ret = 0;
for (int i = 0; i < N; i ++ ) ret += w[i][k];
return ret;
}
void update_mu(int k) {
double up = 0;
for (int i = 0; i < N; i ++ ) up += w[i][k] * input[i];
mu[k] = up / get_tot_w(k);
}
void update_sigma(int k) {
double up = 0;
for (int i = 0; i < N; i ++ ) up += w[i][k] * (input[i] - mu[k]) * (input[i] - mu[k]);
sigma[k] = up / get_tot_w(k);
}
void update_alpha(int k) {
alpha[k] = get_tot_w(k) / N;
}
void train() {
for (int t = 0; t < M; t ++ ) {
// E-Step
for (int i = 0; i < N; i ++ )
for (int k = 0; k < K; k ++ )
update_w(i, k);
// M-Step
// 1. update mu
for (int k = 0; k < K; k ++ ) update_mu(k);
// 2. update sigma
for (int k = 0; k < K; k ++ ) update_sigma(k);
// 3. update alpha
for (int k = 0; k < K; k ++ ) update_alpha(k);
}
}
void output() {
for (int k = 0; k < K; k ++ )
printf("%.5lf %.5lf %.5lf\n", alpha[k], mu[k], sqrt(sigma[k]));
}
int main() {
cin >> K >> N >> M;
for (int i = 0; i < K; i ++ ) {
double a, b, c; cin >> a >> b >> c;
alpha.push_back(a), mu.push_back(b), sigma.push_back(c * c);
}
for (int i = 0; i < N; i ++ ) {
double x; cin >> x;
input.push_back(x);
}
w = vector<vector<double>>(N, vector<double>(K, 0));
train();
output();
return 0;
}

