前言

学了泰勒公式几个月了，最近又有了一些新的理解，我尝逝着用一种非中值定理的方式证明泰勒公式，最后没有成功，但是证明了麦克劳林公式（雾）

这种方式可能会让初学者对泰勒公式有一个比较好的理解，所以整理一篇笔记，可以作为初学者学习泰勒公式的入门文章。

泰勒公式的引入

从近似开始

在函数图像上，我们经常会发现，有些函数的图像长得很像。

如图是$f(x)=\sin x$和$g(x)=x-\frac{x^3}{6}$的图像，在一段范围内，它们几乎是重合的。

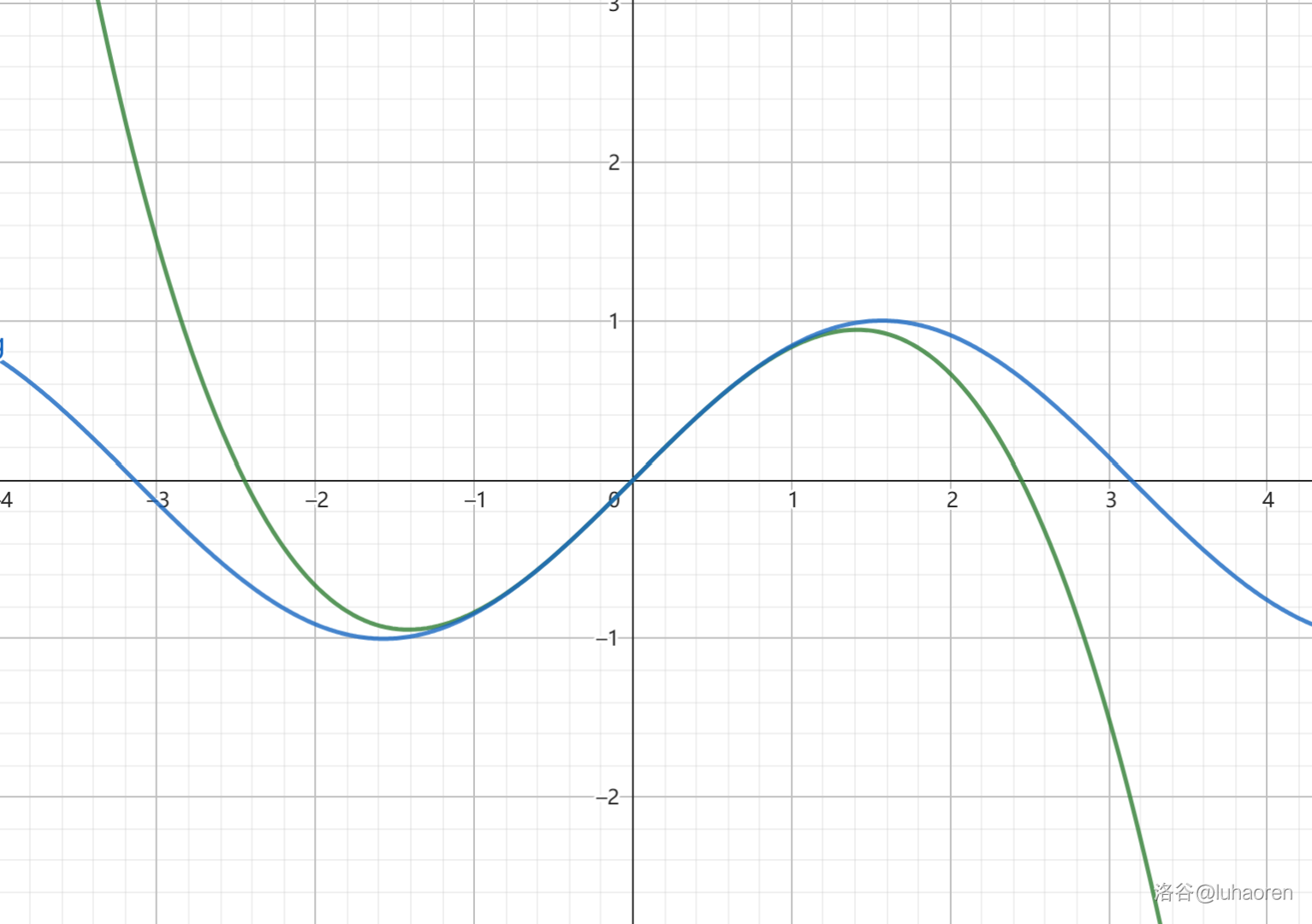
那么，我们能否通过找一个函数的”近似函数“，来研究原函数的性质呢？

比如$\sin$函数，它是一个周期函数，当我们计算一些含有$\sin$函数的极限时，总是很难计算，如果能找一个函数来代替它，那么多方便啊。

而如何找出一个与原函数近似的函数呢？

求导！求导！

现在有一个人，他沿着直线走了一公里，如果我们想完全模仿他的运动过程，该怎么办呢？

首先，我们走的路程应该是一公里，但是这不够，平均速度也得和那个人一样。

平均速度一样也不够，那个人可能走一走停一停，所以加速度也得一样。

除此之外，加速度变化率也得相同，加速度变化率的变化率也得相同，变化率的变化率的变化率还相同……

如果做到这些，那么我们模仿的运动和那个人的运动也就没什么区别了。

聪明的你可能已经看出来了，如果我们想模仿一个函数，那就让它的导数，二阶导数，三阶导数……一直到$n$阶导数都相同，如果这个$n$趋近于无穷，那么模仿出来的函数就和原函数没什么区别了。

初中数学很有用

什么函数最容易求导，求极限呢？当然是多项式函数了，在近似函数的过程中，最方便的办法就是找一个多项式函数来近似。

所以，我们可以先设一个函数$f(x)=a_1+a_2x+a_3x^2+a_4x^3+a_5x^4$（后面先不要），然后先来近似一个函数，比如$\sin$函数。

为了方便求值，我们就把$x=0$代入。

首先，近似函数本身和$\sin$函数的取值应该是相等的，于是我们有

$$ \begin{matrix} a_1 + a_2 \cdot 0 + a_3 \cdot 0 + a_4 \cdot 0 + a_5 \cdot 0 = \sin 0 = 0\\ a_1=0 \end{matrix} $$

然后两个函数分别求导，得到

$$ a_2+2a_3x+3a_4x^2+4a_5x^3=(\sin x)`=\cos x $$

再$x=0$的情况下，有

$$ \begin{matrix} a_2+2a_3\cdot 0+3a_4\cdot 0^2+4a_5\cdot 0^3=1\\ a_2=1 \end{matrix} $$

依次类推，我们能得到一个方程组

$$ \begin{matrix} a_1+a_2x+a_3x^2+a_4x^3+a_5x^4=\sin x \\ a_2+2a_3x+3a_4x^2+4a_5x^3=\cos x \\ 2a_3+6a_4x+12a_5x^2=-\sin x \\ 6a_4+24a_5x=-\cos x \\ 24a_5=\sin x \end{matrix} $$

把$x=0$代入，就有了一个线性方程组
$$ \begin{matrix} a_1=\sin 0=0 \\ a_2=\cos 0=1 \\ 2a_3=-\sin 0=0 \\ 6a_4=-\cos 0=-1 \\ 24a_5=\sin 0=0 \end{matrix} $$

解这个方程组，我们就得到了

$$ \begin{matrix} a_1=0 \\ a_2=1 \\ a_3=0 \\ a_4=-\frac{1}{6} \\ a_5=0 \end{matrix} $$

带回原函数，我们发现我们得出来了一个函数$f(x)=x-\frac{1}{6}x^3$

这就是开头我们引入的那个，和$\sin x$长得很像的函数。

于是，我们发现，通过这样的待定系数法（初中数学 ），我们竟然推导出了一个函数的近似函数。

那么，透过现象看本质，我们能否总结出近似函数的普遍公式呢？

麦克劳林公式

假如我们现在要求一个函数$f(x)$的近似函数，按照刚才的办法，我们先设$g(x)=a_1+a_2x+a_3x^2+a_4x^3+a_5x^4+......+a_nx^{n-1}$

然后列出方程组
$$ \begin{matrix} a_1+a_2x+a_3x^2+a_4x^3+a_5x^4+......+a_nx^{n-1}=f(x) \\ a_2+2a_3x+3a_4x^2+4a_5x^3+......+(n-1)a_nx^{n-2}=f’(x) \\ 2a_3+6a_4x+12a_5x^2+......+(n-2)(n-1)a_nx^{n-3}=f’‘(x) \\ 6a_4+24a_5x+......+(n-3)(n-2)(n-1)a_nx^{n-3}=f^{(3)}(x) \\ \cdots \cdots \\ (n-1)!a_n=f^{(n-1)}(x) \end{matrix} $$

把$x=0$带进去，得到
$$ \begin{matrix} a_1=f(0) \\ a_2=f’(0) \\ 2a_3=f’‘(0) \\ 6a_4=f^{(3)}(0) \\ \cdots \cdots \\ (n-1)!a_n=f^{(n-1)}(0) \end{matrix} $$

于是，我们得到了$g(x)$这个多项式函数各项的系数，也就是

$$ \begin{matrix} a_1=f(0) \\ a_2=f’(0) \\ a_3=\frac{f’‘(0)}{2} \\ a_4=\frac{f^{(3)}(0)}{6} \\ \cdots \cdots \\ a_n=\frac{f^{(n-1)}(0)}{(n-1)!} \end{matrix} $$

于是，我们能得到一个规律：$a_n=\frac{f^{(n-1)}(0)}{(n-1)!}$

所以，
$$ \begin{matrix} g(x)=f(0)+f’(0)x+\frac{f’‘(0)}{2}x^2+\frac{f^{(3)}(0)}{6} x^3+\cdots+\frac{f^{(n-1)}(0)}{(n-1)!}x^{n-1}\\ =\sum_{i=0}^{n}\frac{f^{(i)}(0)}{i!} x^i \end{matrix} $$

这个公式其实就是泰勒公式的一个拓展——麦克劳林公式。

泰勒公式

刚刚我们推导了麦克劳林公式（为什么我不直接推导泰勒公式呢？当然是因为推不出来了），那么泰勒公式又是什么呢？

刚刚我们推导麦克劳林公式时，为了方便直接令$x=0$，而泰勒公式就是$x\ne0$的情况。

泰勒公式的内容如下：
$$ \begin{matrix} f(x)\approx f(x_0)+f’(x_0)(x-x_0)+\frac{f’‘(x_0)}{2}(x-x_0)^2+\frac{f^{(3)}(x_0)}{6} (x-x_0)^3+\cdots+\frac{f^{(n-1)}(x_0)}{(n-1)!}(x-x_0)^{n-1}\\=\sum_{i=0}^{n}\frac{f^{(i)}(0)}{i!} (x-x_0)^i \end{matrix} $$

显然，当$x_0=0$的情况下，得到的公式就是麦克劳林公式。

余项是什么鬼？

在各种高等数学的教科书上，在讲述泰勒公式时都讲了余项这个东西，那么余项是什么呢？

我们说过，泰勒公式的本质是近似，近似总会有误差，余项实际上就是那个误差。

余项一般有两种，分别是拉格朗日余项和皮亚诺型余项。

其中，皮亚诺型余项给的定义是$R_n(x)=o((x-x_0)^n)$，这个很好理解，泰勒公式展开到第$n$项得到的多项式是$\frac{f^{(n)}(0)}{(n)!}(x-x_0)^{n}$，它的更高阶的无穷小就是$o((x-x_0)^n)$，如果$n$足够大的话，这个余项（误差）就非常小。

拉格朗日余项则是 $R_n(x)=\frac{f^{(n+1)}(\xi)(x-x_0)^{n+1}}{(n+1)!}$，它是由拉格朗日中值定理（见我之前的数学笔记）得到的。它主要是来得到第$n$项多项式的误差，通过这个公式，我们能够知道，$x_0$的取值和$x$越接近，误差就越小，所以使用麦克劳林公式有时的精确度就没有那么高。

一些函数的麦克劳林公式

在未来的数学学习中，我们经常需要一些函数的麦克劳林公式，如果“临阵磨枪”，在使用的时候再去推公式，就会耗费很多时间，所以最好记下一些常用函数的展开公式。

$$ e^x=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\cdots+\frac1{n!}x^n{}+o(x^n) $$

$$ \sin x=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\cdots+\frac{(-1)^{m-1}}{(2m-1)!}x^{2m-1}+o(x^{2m-1}) $$

$$ \cos x=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\cdots +\frac{(-1)^m}{(2m)!}x^{2m}+o(x^m) $$

还有一些常用函数的展开式值得记住，如$\ln(1+x)$，$\frac{1}{x+1}$，$\frac{1}{1-x}$，限于篇幅，这里就不展示了。

泰勒公式和麦克劳林公式的应用

求极限

在我之前的数学笔记里讲过洛必达法则，那是一种求极限的方法，但是有的时候我们无法单纯通过洛必达法则求出极限，这时候就需要配合泰勒公式使用。

比如这道题
$$ \lim_{\Delta x\to 0} \frac{x-\sin x}{x^3} $$

这道题我们当然可以使用洛必达法则，但是那需要洛很多次（其实很方便 ），在本题中我们使用泰勒公式。

首先，我们发现函数如果没有$\sin x$，那就变成了一个多项式函数，所以关键是把$\sin x$展开掉。

那么展开几阶呢？

我们都知道
$$ \begin{matrix} \sin x\sim x+o(x)\\ \sin x \sim x-\frac{1}{3!}x^3+o(x^3)\\ \sin x\sim x-\frac{1}{3!}x^3+\frac{1}{5!}x^5+o(x^5) \end{matrix} $$

（其中，第一个展开式其实就是等阶无穷小，所以等价无穷小的实质就是泰勒展开的低阶形式）

在本题中，我们发现分式底下是$x^3$是三次项，在求极限时，上下应该是同阶的，所以我们展开到$\frac{1}{3!}x^3$就够用了。

因此我们得到了
$$ \begin{matrix} \lim_{\Delta x\to 0} \frac{x-x+\frac{1}{3!}x^3+o(x^3)}{x^3} \\ =\lim_{\Delta x\to 0} \frac{\frac{1}{3!}x^3}{x^3}\\ =\frac{1}{6} \end{matrix} $$

总结一下，泰勒公式求极限的方式。

1. 一般是乘除的时候才使用泰勒公式，如果是加减的话对精度的要求比较高，尽量不要使用。
2. 如果是分式，上下展开的最高阶数应该相同。
3. 最好在运算的过程中写一下皮亚诺余项（就是那个$o(x^3)$），它可以帮你确定展开的精度够不够用。