更好的阅读体验

前言

今天学了微分中值定理，感觉很难，整理一下证明和例题，希望能掌握更牢固。

本文介绍Rolle，Lagrange，Cauchy三个定理，事实上，这三者的关系互相包含（前一项是后一项的特例），但又都很重要，在OI中可能会有一些应用（我也不知道有什么应用）

1. Rolle定理

Rolle定理是最基础的中值定理，比较直观，是最好理解的。

定义

设函数$f(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$上可导，且$f(a)=f(b)$，则在$(a,b)$上至少存在一点$x_0$，使

$$f’(x_0)=0$$

分析

这个定理很好理解，以运动为例，想想一个物体运动，从起始点出发，运动一会又回到了起始点，那么在这个过程中，这个物体肯定有一个时候速度是0。

如果画出s-t图像，那么速度就是斜率（也就是导数），我们会发现刚刚举的例子就是Rolle定理在$f(a)=f(b)=0$时的特例，而这个特例很容易推广到整体。

如图，这是一个二次函数的图像，当在函数顶点时，$f’(x)=0$

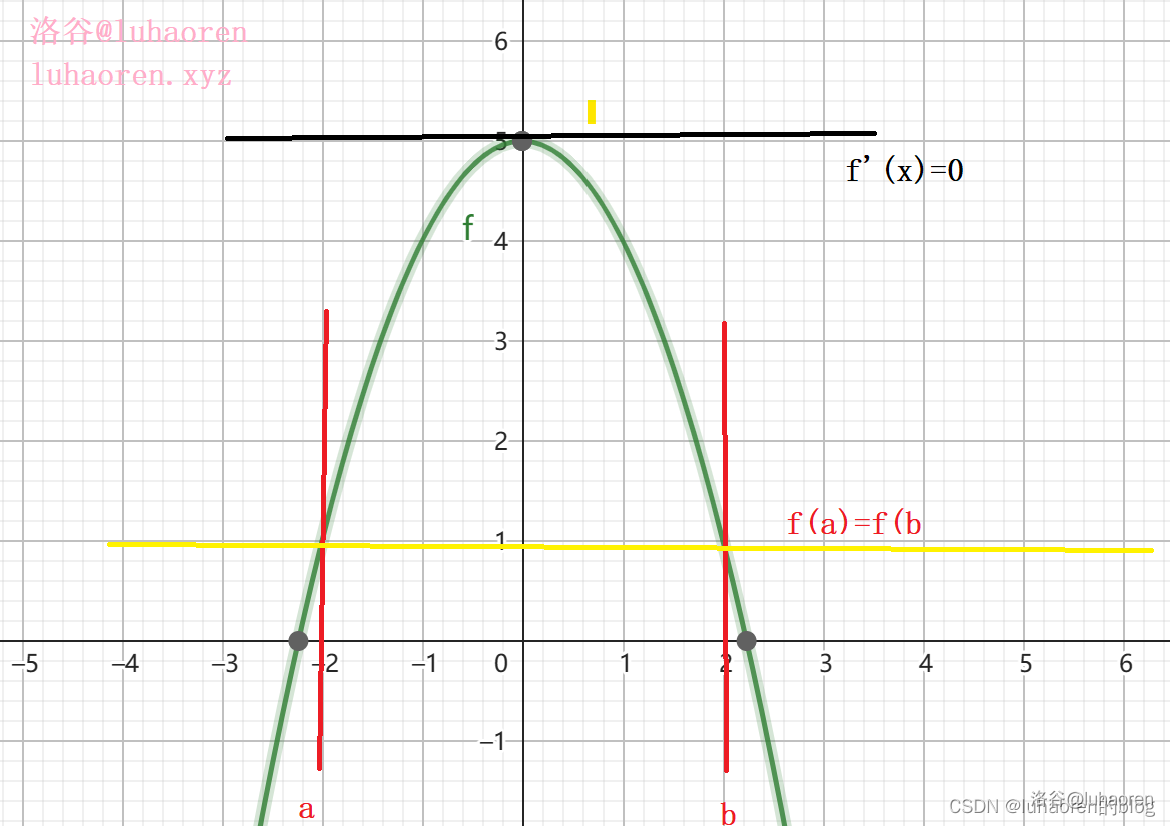
证明

正经的证明不会，口胡一个。

我们有函数$f(x)$满足在区间$[a,b]$内连续可导，且$f(a)=f(b)$

对$f(x)$分类讨论。

若$f(x)$为常函数，则$f(x)$为一条平行于$x$轴的直线，斜率为0。

否则，

因为$f(a)=f(b)$，所以$f(x)$不为一次函数。

因为$f(x)$在区间$[a,b]$内连续，所以$f(x)$必有拐点（峰值或谷值）。

在拐点处$f(x_0)$的斜率为0。

故在$(a,b)$上至少存在一点$x_0$，使$f’(x_0)=0$

注意事项

Rolle定理的三个条件（连续，可导，$f(a)=f(b)$）都要满足才能应用Rolle定理，否则很可能不成立。

如图，函数$f(x)=|x|$在$(1,-1)$区间内，不满足连续性，所以在区间内没有一点的导数为0。

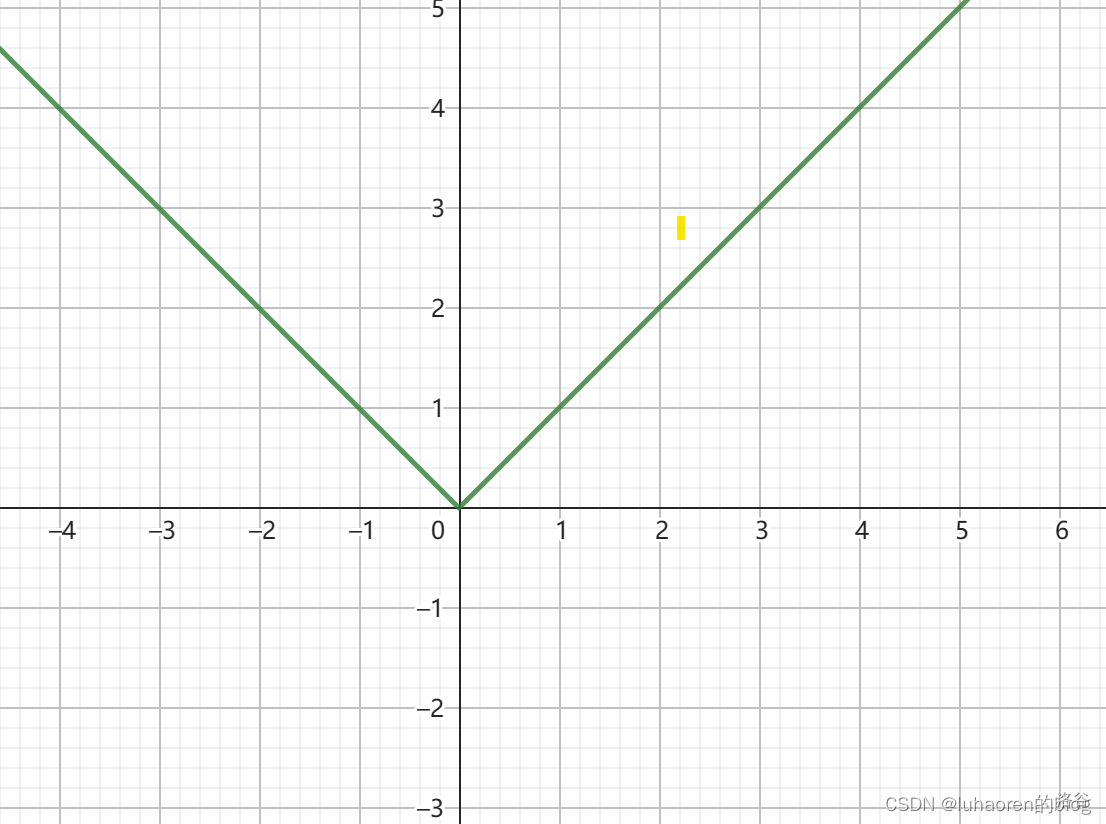
应用

如果$f(x)=0$，说明什么？

说明f(x)这个方程至少有一个实根。

如果我们遇到求一个方程在区间内有没有实根的题，就可以用Rolle定理。

解题思路：

首先构造一个$F(x)$，让它的导函数为$f(x)$（实际上就是求$f(x)$的积分）

然后证明$F(a)=F(b)$（ab是区间左右边界）

之后只需说明$F(x)$在区间内是连续可导的，就可以应用Rolle定理，使区间内必有一个数$x_0$，使$F’(x)=0$（即$f(x)=0$）

例题

例题1
证明Rolle定理对函数$f(x)=x^2-2x$在区间$[0,2]$上的正确性。

证明：

因为$f(x)$是多项式，所以$f(x)$连续可导，且$f(0)=f(2)=0$

故满足Rolle定理的基本条件。

$f’(x)=2x-2$

令$f’(x_0)=0$，即$2x_0-2=0$，得$x_0=1$

因为$1 \in[0,2]$

$\therefore \exists x \in [0,2]$使得$f’(x)=0$

例题2
证明方程$4x^3-6x^2+2x$在开区间$(0,1)$内至少有一个实根。

证明：

设$F(x)=x^4-2x^3+x^2$

则$F(x)$在$[1,0]$上连续，在$(1,0)$上可导。

此时$F(0)=0$，$F(1)=0$

由Rolle定理，在$(0,1)$上必存在$x_0$，使得$F’(x_0)=0$

即$\exists x \in (0,1)$，使得$4x^3-6x^2+2x$

即$4x^3-6x^2+2x$在$(0,1)$内有实根

2. Lagrange中值定理

定义

$\exists x_0 \in (a,b)$，满足$f(x)$在$[a,b]$上连续，在$(a,b)$上可导，有$f’(x_0)=\frac{f(b)-f(a)}{b-a}$

证明

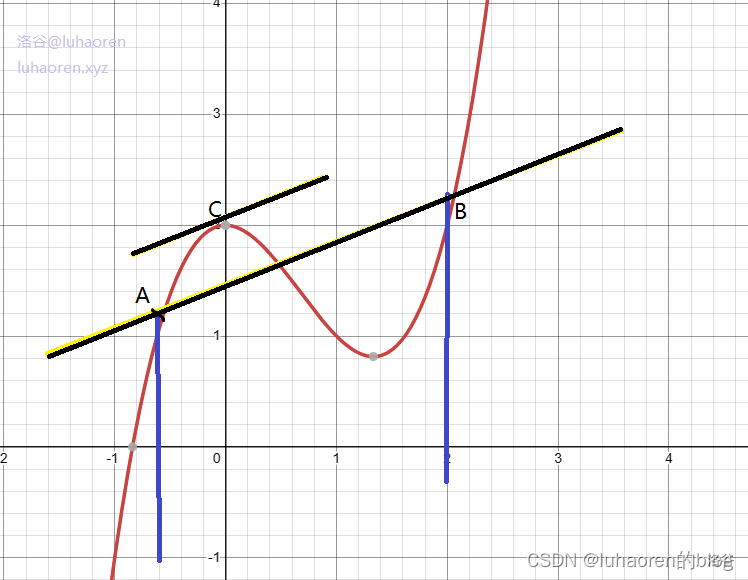
作直线$g(x)$过$A,B$

由点斜式方程得$g(x)=f(a)+\frac{f(b)-f(a)}{b-a} (x-a)$

设$F(x)=g(x)-f(x)$

$=f(a)+\frac{f(b)-f(a)}{b-a} (x-a)-f(x)$

$F(a)=f(a)-f(a)+\frac{f(b)-f(a)}{b-a} (a-a)=0$

$F(b)=f(a)- f(b)+\frac{f(b)-f(a)}{b-a}(b-a)=0$

且$F(x)$在$[a,b]$上连续，在$(a,b)$上可导。

应用Rolle定理，

则在$(a,b)$上必有一点$x_0$，使得$F’(x)=0$

即$g’(x)-f’(x)=0$，即$g’(x)=f’(x)$

$g’(x)=\frac{f(b)-f(a)}{b-a}$

故得$f’(x)=\frac{f(b)-f(a)}{b-a}$

证毕

分析

Lagrange中值定理实际上是Rolle定理的推论。

$f’(x_0)=\frac{f(b)-f(a)}{b-a}$

当$f(b)=f(a)$时，$\frac{f(b)-f(a)}{b-a}$，即$f’(x_ 0)=0$，即Rolle中值定理。

推论

推论1

若$f(x)$在$(a,b)$上连续可导，且$f’(x) \equiv 0$，则$f(x)$为常函数

其实就是常函数的导数是0，看起来是个常识，但也可以证明。

证明

设$x_1,x_2 \in(a,b)$

由Lagrange中值定理，

$\exists x_0 \in(x_1,x_2)$，使得$f’(x_0)=\frac{f(b)-f(a)}{b-a}$

即$f’(x_0)(b-a)+f(a)-f(b)=0$

$∵f’(x) \equiv0$

故$f(a)-f(b)=0$

即$f(a)=f(b)$

即证$f(x)$是常函数

推论2

如果$f’(x)=g’(x)$，那么存在常数$C$，使得$f(x)=g(x)+C$成立

这个推论可以用上个推论来证

证明

令$F’(x)=g’(x)-f’(x)=0$

由推论1，$F(x)= C$

故$g(x)-f(x)=C$

即$f(x)=g(x)+C$

3. Cauchy中值定理

定义

有函数$f(x),g(x)$在$(a,b)$连续可导

$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f’(x_0)}{g(x_0)}$$

证明

不会证

分析

事实上，Cauchy中值定理是Lagrange中值定理的推广形式。

若$g(x)=x$，则原式可化为$f’(x_0)=\frac{f(b)-f(a)}{b-a}$，即Lagrange中值定理