计数

无根树有序点：$n^{n-2}$

有根数有序点：$n^{n-2}*n$

$CR: H(n,m)=(n+m-1)!/((n-1)!m!)$

二叉树：$n_0=n_2+1$

群：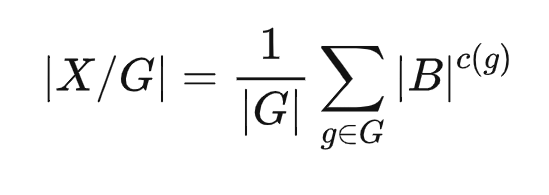

阅读程序（问题解决）

归并排序第k小

#include <bits/stdc++.h>
using namespace std;

int solve(int *a1, int *a2, int n, int k) {
    int left1 = 0, right1 = n - 1;
    int left2 = 0, right2 = n - 1;
    while (left1 <= right1 && left2 <= right2) {    // 双指针
        int m1 = (left1 + right1) >> 1;
        int m2 = (left2 + right2) >> 1;
        int cnt = m1 + m2;  // 计数
        if (a1[m1]<=a2[m2]) {   
            if (cnt < k) left1 = m1 + 1; // 左扩展
            else right2 = m2 - 1;   // 右收敛
        } else {
            if (cnt < k) left2 = m2 + 1;
            else right1 = m1 - 1;
        }
    }
    if (left1 > right1) {   // 左扩展完
        if (left1 == 0) {
            return a2[k - 1];   // 左无
        } else {
            int x = a1[left1 - 1], y = a2[k - left1 - 1]; // 比较
            return std::max(x, y);
        } 
    } else {
            if (left2 == 0) {
                return a1[k - 1];
            } else {
                int x = a2[left2 - 1], y = a1[k - left2 - 1];
                return std:: max(x, y);
            }
    }
}

(2)（容器分水） 有两个容器，容器 1 的容量为为 a 升，容器 2 的容量为 b 升；同时允许下列的三种操作，分别为：

FILL(i)：用水龙头将容器 (∈1,2) 灌满水；
DROP(i)：将容器 i 的水倒进下水道；
POUR(i,j)：将容器 i 的水倒进容器 j（完成此操作后，要么容器 j 被灌满，要么容器 i 被清空）。
求只使用上述的两个容器和三种操作，获得恰好 c 升水的最少操作数和操作序列。上述 a、b、c 均为不超过 100 的正整数，且 c≤max{a,b}。

试补全程序。

#include <bits/stdc++.h>
using namespace std;
const int N = 110;

int f[N][N];
int ans;
int a, b, c;
int init;

int dfs(int x, int y) {
    if (f[x][y] != init)
        return f[x][y];
    if (x == c || y == c)
        return f[x][y] = 0;
    f[x][y] = init - 1;
    f[x][y] = min(f[x][y], dfs(a, y) + 1);
    f[x][y] = min(f[x][y], dfs(x, b) + 1);
    f[x][y] = min(f[x][y], dfs(0, y) + 1);
    f[x][y] = min(f[x][y], dfs(x, 0) + 1);
    int t = min(a - x, y);
    f[x][y] = min(f[x][y], dfs(x + t, y - t) + 1);// a倒b
    t = min(x, b - y);
    f[x][y] = min(f[x][y], dfs(x - t, y + t) + 1);// b倒a
    return f[x][y];
}

void go(int x, int y) { // 路径回溯
    if (x == c || y == c)   //结束
        return;
    if (f[x][y] == dfs(a, y) + 1) {
        cout << "FILL(1)" << endl;
        go(a, y);
    } else if (f[x][y] == dfs(x, b) + 1) {
        cout << "FILL(2)" << endl;
        go(x, b);
    } else if (f[x][y] == dfs(0, y) + 1) {
        cout << "DROP(1)" << endl;
        go (0, y);
    } else if (f[x][y] == dfs(x, 0) + 1) {
        cout << "DROP(2)" << endl;
        go(x, 0);
    } else {
        int t = min(a - x, y);
        if(f[x][y] == dfs(x + t, y - t) + 1) {
            cout << "POUR(2,1)" << endl;
            go(x + t, y - t);
        } else {
            t = min(x, b - y);
            if (f[x][y] == dfs(x - t, y + t) + 1) {
                cout << "POUR(1,2)" << endl;
                go(x - t, y + t);
            } else
                assert(0);
        }
    }
}

int main() {
    cin >> a >> b >> c;
    ans = 1 << 30;
    memset(f, 127, sizeof f);
    init = **f;
    if ((ans = dfs (0, 0)) == init - 1)
        cout << "impossible";
    else {
        cout << ans << endl;
        go (0, 0);
    }
}

四毛子

#include <stdio.h>
#include <math.h>
#define MAXN 20000000
#define MAXT (MAXN<<1)
#define MAXL 18
#define MAXB 9
#define MAXC (MAXT/MAXB)
struct node{
    int val, dep, dfn, end;
    struct node *son[2];//son[0],son[1]分别表示左右儿子
}T[MAXN], *root, *id[MAXT], *Min[MAXL][MAXC];
struct node*min(struct node *x, struct node *y){return x->dep<y->dep?x:y;}
int n, t, b, c, Log2[MAXC+1];
int Pos[(1<<(MAXB-1))+5], Dif[MAXC+1];
void build(){//建立Cartesian树
    static struct node*S[MAXN+1];//单调栈 
    int top=0;
    for(int i=0; i<n; i++){
        struct node *p=&T[i];
        while(top&&S[top]->val<p->val)
            p->son[0]=S[top--];
        if(top) S[top]->son[1]=p;//右儿子在最后才连，这样就没必要把之前 pop 掉的儿子修改， 
        S[++top]=p;
    }
    root=S[1];
}
void DFS(struct node *p){//构建 Euler序列(dfs 环游序)
    id[p->dfn=t++]=p;
    for(int i=0; i<2; i++)
        if(p->son[i]){
            p->son[i]->dep=p->dep+1;
            DFS(p->son[i]);
            id[t++]=p;
        }
    p->end=t-1;
}
void ST_init(){//大块 ST 表预处理 
    b=(int)(ceil(log2(t)/2));//块长logn/2
    c=t/b;//总共多少块 
    Log2[1]=0;
    for(int i=2; i<=c; i++)
        Log2[i]=Log2[i>>1]+1;
    for(int i=0; i<c; i++){//先找出每一块内部最小值 
        Min[0][i]=id[i*b];
        for(int j=1; j<b; j++)
            Min[0][i]=min(Min[0][i], id[i*b+j]);
    }
    for(int i=1, l=2; l<=c; i++, l<<=1) //ST 表 
        for(int j=0; j+l<=c; j++)
            Min[i][j]=min(Min[i-1][j], Min[i-1][j+(l>>1)]);
}
void small_init(){//块内预处理
    for(int i=0; i<=c; i++)
        for(int j=1; j<b&&i*b+j<t; j++)//记录差分数组 Dif 
            if(id[i*b+j]->dep<id[i*b+j-1]->dep) Dif[i]|=1<<(j-1);
    for(int S=0; S<(1<<(b-1)); S++){
        //计算状态 S 的最大值应该落在第几个位置 
        int mx=0,v=0;
        for(int i=1; i<b; i++){
            v+=(S>>(i-1)&1)?-1:1;
            if(v<mx) mx=v, Pos[S]=i;
        }
    }
}
struct node*ST_query(int l,int r){//对于整块使用 ST 表 
    int g=Log2[r-l+1];
    return min(Min[g][l],Min[g][r-(1<<g)+1]);
}
struct node*small_query(int l, int r){//块内查询
    int p=l/b;//第几个块 
    int S=(Dif[p]>>(l-p*b))&((1<<(r-l))-1);
    //将 [L[p], l-1], [r+1, R[p]] 多出来的清理掉 
    return id[l+Pos[S]];
}
struct node*query(int l, int r){
    if(l>r) return query(r,l);
    int pl=l/b, pr=r/b;
    if(pl==pr) return small_query(l,r);//同一块内 
    else{
        struct node *s=min(small_query(l, pl*b+b-1), small_query(pr*b,r));//询问散块 
        if(pl+1<=pr-1) s=min(s, ST_query(pl+1,pr-1));//中间的整块 
        return s;
    }
}
int main(){
    int m;
    scanf("%d%d", &n, &m);
    for(int i=0; i<n; i++)
        scanf("%d", &T[i].val);
    build();
    DFS(root);
    ST_init();
    small_init();
    while(m--){
        int l,r;
        scanf("%d%d", &l, &r);
        printf("%d\n", query(T[l-1].dfn, T[r-1].dfn)->val);
    }
    return 0;
}

虽说这类题最好用dfs做，但本算法具体来说就是最短路迭代。

#include <iostream>

using namespace std;

typedef long long LL;

const int MAXN = 40000, M = 16, B = M >> 1, MS = (1 << B) - 1;
const LL INF = 1000000000000000LL;
LL Max[MS + 4][MS + 4];

int w(int x) 
{
    int s = x;
    while(x) 
    {
        x ^= x &(x ^ (x - 1));
        s++;
    }
    return s;
}

void to_max(LL &x, LL y) 
{
    if(x < y)
        x = y;
}

int main() 
{
    int n;
    LL ans = 0;
    cin >> n;
    for(int x = 0; x <= MS; x++)
        for(int y = 0; y <= MS; y++)
            Max[x][y] = -INF;
    for(int i = 1; i <= n ; i++) 
    {
        LL a;
        cin >> a;
        int x = a >> B , y = a & MS;
        LL v = 0;
        for(int z = 0; z < = MS; z++)
            to_max(v, Max[x][z] + w(y ^ z));
        for(int z = 0; z < = MS; z++)
            to_max(Max[z][y], v + w((x ^ z) << B));
        to_max(ans , v);
    }
    cout << ans << endl;
    return 0;
}

DP优化思想，分部处理。

#include <cstdio>
using namespace std;

const int maxn = 1005;

int n, B, w[maxn], v[maxn];

int gcd(int u, int v) {
    if (v == 0)
        return u;
    return gcd(v, u % v);
} 

void print(int w, int v) {
    int d = gcd(w, v);
    w = w / d;
    v = v / d;
    if (v == 1)
        printf("%d\n", w);
    else
        printf("%d/%d\n" w, v);
}
void swap(int &x, int &y) {
    int t = x; x = y; y = t;
}

int main() {
    scanf("%d %d" &n, &B);
    for (int i = 1; i <= n; i ++) {
        scanf("%d %d", &w[i], &v[i]);
    }
    for (int i = 1; i < n; i ++)
        for (int j = 1; j < n; j ++)
            if (w[j] * v[j+1] < w[j+1] * v[j]) {
                swap(w[j], w[j + 1]);
                swap(v[j], v[j + 1]);
            }
    int curV, curW;
    if  (v[1] <= B) {
        curV = v[1]; curW = w[1];
    } else {
        print(B * w[1] , v[1]);
        return 0;
    }
    for (int i = 2; i <= n; i ++)
        if (curV + v[i] <= B) {
            curV += v[i];
            curW += w[i];
        } else {
            print (curW * v[i] + (B - curV) * w[i], v[i]);
            return 0;
        }
    print(curW, 1);
    return 0;
}

分数背包（贪心）

#include <cstdio>
#include<algorithm>
using namespace std;
const int maxn = 64;
int n, m;
int a[maxn], b[maxn];
unsigned long long status, trans;
bool win;
int main(){
    scanf("%d%d", &n, &m);
    for (int i = 0; i < n; ++i)
        scanf("%d%d", &a[i], &b[i]);
    for(int i = 0; i < n; ++i)
        for(int j = i + 1; j < n; ++j)
            if (a[i] > a[j]){
                swap(a[i], a[j]);
                swap(b[i], b[j]);
            }
    status = ~0ull^1;
    trans = 0;
    for(int i = 1, j = 0; i <= m; ++i){
        while (j < n && a[j] == i){
            trans |=1ull << (b[j] - 1);
            ++j;
        }
        win = ~status & trans;
        status = status << 1 ^ win;
    }
    puts(win ? "Win" : "Loss");
    return 0;
}   

通过二进制压缩状态处理的博弈论。

#include<cstdio>
using namespace std;
const int maxn = 1001;

int n;
int cnt[maxn];
int child [maxn][maxn];
int unlock[maxn];
int threshold[maxn], bonus[maxn];
int points;
bool find(){
    int target = -1;
    for (int i = 1; i <= n; ++i)
        if(unlock[i] == 0 && points >= threshold[i]){
            target = i;
            break;
    }
    if(target == -1)
        return false;
    unlock[target] = -1;
    points += bonus[target];
    for (int i = 0; i < cnt[target]; ++i)
        unlock[child[target][i]] -= 1;
    return true;
}

int main(){
    scanf("%d%d", &n, &points);
    for (int i = 1; i <= n; ++i){
        cnt[i] = 0;
        scanf("%d%d", &threshold[i], &bonus[i]);
    }
    for (int i = 1; i <= n; ++i){
        int m;
        scanf("%d", &m);
        unlock[i] = m;
        for (int j = 0; j < m; ++j){
            int fa;
            scanf("%d", &fa);
            child[fa][cnt[fa]] = i;
            ++cnt[fa];
        }
    }

    int ans = 0;
    while(find())
        ++ans;

    printf("%d\n", ans);
    return 0;
}

拓扑问题