更好的阅读体验
原题链接

题目描述

H 国有 n 个城市，这 n 个城市用 n-1 条双向道路相互连通构成一棵树，1号城市是首都，也是树中的根节点。

H 国的首都爆发了一种危害性极高的传染病。

当局为了控制疫情，不让疫情扩散到边境城市（叶子节点所表示的城市），决定动用军队在一些城市建立检查点，使得从首都到边境城市的每一条路径上都至少有一个检查点，边境城市也可以建立检查点。

但要注意的是，首都是不能建立检查点的。

现在，在H国的一些城市中已经驻扎有军队，且一个城市可以驻扎多个军队。

军队总数为 m 支。

一支军队可以在有道路连接的城市间移动，并在除首都以外的任意一个城市建立检查点，且只能在一个城市建立检查点。

一支军队经过一条道路从一个城市移动到另一个城市所需要的时间等于道路的长度（单位：小时）。

请问：最少需要多少个小时才能控制疫情？

注意：不同的军队可以同时移动。

输入格式

第一行一个整数n，表示城市个数。

接下来的n-1行，每行3个整数，u、v、w，每两个整数之间用一个空格隔开，表示从城市u到城市v有一条长为w的道路，数据保证输入的是一棵树，且根节点编号为1。

接下来一行一个整数m，表示军队个数。

接下来一行m个整数，每两个整数之间用一个空格隔开，分别表示这m个军队所驻扎的城市的编号。

输出格式

共一行，包含一个整数，表示控制疫情所需要的最少时间。如果无法控制疫情则输出-1。

数据范围

$2 \le m \le n \le 50000$,
$0 < w < 10^9$

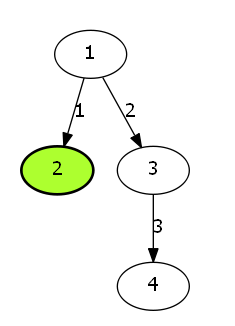
输入样例：

4
1 2 1
1 3 2
3 4 3
2
2 2

输出样例：

3

样例图片

解题报告

题意理解

有一种传染病,叫做延迟快乐. by 秦淮岸灯火阑珊

Acwing网站,我们形象地认为它是一棵$n-1$个节点的树.

现在从根节点(yxc直播间)处出现了这样的一种名为延迟快乐的传染病.他会感染整棵树.

已知现在有$m$名管理员,他们希望为了不让新来的成员们(叶子节点)也感染到这种延迟快乐感染病,于是他们会分别驻守在一些直播间.

(你可以认为每一个直播间就是一个节点,而一个大直播间是由很多小直播间构成,这是为什么,我也不知道.)

每两个直播间,有一条链接,而不同的链接,他们需要消耗的流量是不一样的.

每个管理员刚开始呆在不同的直播间.他们可以在和自己所在直播间相连的直播间互相穿梭.

现在希望流量消耗最大的管理员消耗流量最小,使得这种传染病不会传染到新成员(叶子节点)身上.

不能在根节点处驻守管理员.因为站长yxc拥有最高权限,现在他也被延迟快乐感染了.其他管理员为了不被感染,不能抵达yxc直播间

如果说不可能防止延迟快乐传染病,那么我们只能输出$-1$.

最强广告宣传委员

感觉好懵逼啊,我们还是乖乖看原题意吧.

算法解析

贪心性质·往上走

我们来认认真真地分析这道题目,蕴含的巨多性质.

1. 所有的管理员,往越高级的直播间走越好.

正经语言说,就是所有的控制节点,尽量往树的根节点走.

这是为什么呢.

我们知道一个管理员,他面临着三大选择.

往上走奋发向上,往下走不思进取,不走.懒人

我们的Acwing管理员,个个都是奋发向上的大佬,他们肯定会往上走.

但是,这是为什么呢?

一个管理节点,他可以控制的范围,其实就是他的子树.

因为延迟快乐传染病是从根节点而来的.

而每一个节点,其实都是根节点到他的子树节点们的唯一通道.可以说是唯一中间商.

所以我们越往上走,子树节点越多,那么管理范围越大.

这就是我们的第一个贪心性质.

单调性质·多流量

假如说我们最有钱(消耗流量最多)的管理员,他消耗的流量是$x$GB.完成了任务.

那么我们给这个管理员$x+250G$的流量,他当然也可以完成任务.

但是我们如果给他$x-1G$的流量,那么他一定不可能完成任务.

综上所述,总而言之,我们得到了,单调性质

假如说我们的答案是x,那么x-0.233一定不可以完成任务,x+0.233一定可以完成任务.

分类性质·两种人

我们发现,其实所有的管理员可以分成两组.

1. 能够抵达根节点下面的儿子节点
2. 不能够抵达根节点下面的儿子节点

我们发现,如果一位管理员属于第二种类型的管理员,也就是尽我所能的管理员,那么显然他就抵达自己能够抵达的深度最浅的节点即可.

根据上面的贪心性质可以得到,子树节点越多,那么管理范围越大,想让我们是要让管理范围越大越好.,因此管理员越往上面走,越好不过了,毕竟管理空间就越大了.

接下来我们着重分析,第一类管理员,简称学有余力的管理员,那么我们发现这位管理员,面临着人生的两大选择.

1. 安分守己,管理自己这棵子树的一亩三分地.也就是不动明王,不做任何改动,依旧呆在这个节点.
2. 转移职场,把握住一切可以控制的机会,离开自己这个节点,通过根节点,走到其他节点,管理另外一棵子树..

其实我们还可以理解,一个是安分守己地在原公司工作,另外一个则是跳槽换到另外一个公司.

当前问题就是,我们如何判断一位管理员,是该安分守己,还是该转移职场.

我们应该有一个评判依据.

我们先来好好看一张图片.

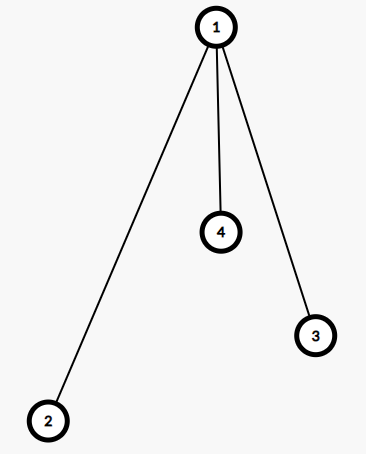
观察这张图片,我们非常清楚地发现.
$$ dis[1->2]>dis[1->3]>dis[1->4] \\\\ dis[a->b]表示节点a到节点b的距离 $$
假如说现在,$2$和$3$这两个节点上面有管理员,然而节点$4$上面没有管理员,需要派遣管理员.

我们到底是派遣哪一个节点上的管理员去比较好呢?
$$ 如果处于2号节点的管理员他还有cnt \quad GB的流量 \\\\ 但是cnt < dis[1->2]+dis[1->2] $$
那么这位管理员,绝对不能够动,现在他处于极其重要的战略位置.

假如说这位管理员转移到其他节点的话,那么一定是转移到$4$号节点,因为
$$ dis[2->1]<dis[1->4] $$
这样我们才能够在流量不欠费的前提下,抵达目标节点.

但是我们知道目标节点,其实还可以由$3$号节点转移过来的,而且消耗的时间更加少.

那么我们把$4$号节点留给其他人,可能性更加多.

或者我们这样形象理解,这个节点上,如果这位管理员走了,那么必须有另外一个管理员跨越根节点来填补,这样显然不够优秀,因为另外一个管理员不如驻守$4$号节点,然后这位管理员停留下来,这样的花费更加少,更加优秀,

总而言之,言而总之,我们确定了以下方案.

对于需要驻扎的节点,我们派遣剩余流量越少的管理员去管理离根节点越近节点(前提是,这个管理员可以抵达这个节点).

也就是能力小的管理员,就管理消耗小的节点,能力大的管理员,就去管理消耗大的节点.

总结流程

1. 倍增跳跃,使得所有节点尽量快速往上爬

2. 二分判断,最小化最大消耗时间.

3. 贪心分配,使得物尽其能.

代码解析

#include <bits/stdc++.h>
using namespace std;
#define mk(a,b) make_pair(a,b)
const int N=50000+200;
int head[N<<1],ver[N<<1],Next[N<<1],edge[N<<1],tot;
int deep[N],fa[N][22],cnt,n,m,a[N],sum;
int tot2,tot3,tot4,t;
long long dis[N][22],Free[N],need2[N];
bool vis[N],okk,need[N];
pair<long long,int> h[N];//可以抵达根节点的节点
struct Edge
{
    inline void init()
    {
        memset(head,0,sizeof(head));
        tot=0;
    }
    inline void add_edge(int a,int b,int c)
    {
        edge[++tot]=b;
        ver[tot]=c;
        Next[tot]=head[a];
        head[a]=tot;
    }
    inline void bfs()
    {
        queue<int> q;
        q.push(1);
        deep[1]=1;
        while(q.size())
        {
            int x=q.front();
            q.pop();
            for(int i=head[x]; i; i=Next[i]) //遍历x的出边
            {
                int y=edge[i];//出边
                if(deep[y])//已经访问过了 ,其实就是父亲节点
                    continue;//若深度小于当前节点，说明是当前节点的父节点
                deep[y]=deep[x]+1;//深度+1,儿子节点是y,父亲节点是x
                fa[y][0]=x,dis[y][0]=ver[i];//DP状态
                for(int j=1; j<=t; j++)
                {
                    fa[y][j]=fa[fa[y][j-1]][j-1];
                    dis[y][j]=dis[y][j-1]+dis[fa[y][j-1]][j-1];
                }//DP
                q.push(y);
            }
        }
    }
    inline bool dfs(int x)
    {
        bool ok=false;//判断是不是叶子节点,false为叶子,true为非叶子节点
        if (vis[x])//已经控制了
            return true;
        for(int i=head[x]; i; i=Next[i])//访问所有的出边
        {
            int y=edge[i];//出边节点
            if (deep[y]<deep[x])//比自己深度小的节点,那就是自己的父亲节点
                continue;
            ok=true;//既然有儿子节点了,那么一定不是叶子节点
            if (!dfs(y))//有叶子节点没有被控制,自己肯定也就不会被控制了
                return false;
        }
        if (!ok)//这个节点是叶子节点,而且没有被控制
            return false;
        return true;//所有叶子节点都被控制
    }
    inline bool check(long long s)
    {
        memset(h,0,sizeof(h));
        memset(need,0,sizeof(need));
        memset(vis,false,sizeof(vis));
        memset(need2,0,sizeof(need2));
        memset(Free,0,sizeof(Free));
        tot2=tot3=tot4=0;
        for(int i=1; i<=m; i++) //分类
        {
            long long ans=0,x=a[i];
            for(int k=t; k>=0; k--) //倍增跳跃
                if (fa[x][k]>1 && ans+dis[x][k]<=s)//找到最高能跳到哪里,且不会跳到根节点
                    ans+=dis[x][k],x=fa[x][k];//累加路径长度,并且跳跃
            if (fa[x][0]==1 && ans+dis[x][0]<=s)//跳到了根节点的儿子节点,有剩余时间
                h[++tot2]=mk(s-(ans+dis[x][0]),x);//剩余时间,当前位置
            else
                vis[x]=true;//位置x已经访问
        }
        for(int i=head[1]; i; i=Next[i])
            if (!dfs(edge[i]))
                need[edge[i]]=true;//开始遍历整棵树,康康有哪些节点没有被控制
        sort(h+1,h+1+tot2);//从小到大排序,剩余时间(第一维)
        for(int i=1; i<=tot2; i++) //空闲节点开始出发
            if (need[h[i].second] && h[i].first<dis[h[i].second][0])//你所在的节点需要控制,你抵达不了根节点,而且返回.
                need[h[i].second]=0;//去除标记,这支军队不动,继续驻守
        //我们之前已经剪掉过一次 详情请见s-(ans+dis[x][0]),所以这一次只要比较一下.就是剪掉两次的意思.
            else//可以调动
                Free[++tot3]=h[i].first;//存储空余时间 ,军队可以调动
        for(int i=head[1]; i; i=Next[i])
            if (need[edge[i]])//这个节点需要控制
                need2[++tot4]=dis[edge[i]][0];//需要控制的时间
        if (tot3<tot4)//军队不够用
            return false;
        sort(Free+1,Free+1+tot3);//军队按照空余时间(能力)从小到大排序
        sort(need2+1,need2+1+tot4);//需要驻守节点按照所需代价从小到大排序(驻守就是控制的意思)
        int i=1,j=1;//i表示需要驻守节点,j表示当前军队
        while(i<=tot4 && j<=tot3)//军队没有用完,节点没有走完
            if (Free[j]>=need2[i])
                i++,j++;
            else
                j++;
        if (i>tot4)//全部都驻守完了
            return true;
        else
            return false;
    }
    inline long long Point(void)
    {
        long long l=1,r=sum,mid=0;//二分边界
        while(l<r)
        {
            mid=l+r>>1;
            if (check(mid))
            {
                r=mid;
                okk=true;
            }
            else
                l=mid+1;
        }
        return r;
    }
} g1;
int main()
{
    g1.init();
    scanf("%d",&n);
    for(int i=1; i<n; i++)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        g1.add_edge(a,b,c);
        g1.add_edge(b,a,c);
        sum+=c;//统计所有边权之和
    }
    scanf("%d",&m);
    for(int i=1; i<=m; i++)
        scanf("%d",&a[i]);
    okk=false;
    t=log2(n)+1;
    g1.bfs();
    long long ans=g1.Point();
    printf("%lld\n",okk?ans:-1);
    return 0;
}