更好的阅读体验

前言

本来想学完回滚莫队、树上莫队、二离莫队之后一起写一个博客，但是一直学不会/kk，只好把已会的普通莫队和带修莫队写了（以后会补上的）

普通莫队

莫队——优雅的暴力

莫队算法的引入

例题：

给定一个数列和若干询问，每次询问询问一段区间内不同种类数字的个数。

暴力做法

每次询问暴力枚举区间$[l,r]$，用一个数组$cnt$记录每个数在区间内出现的次数，最后枚举$cnt$数组，记录所有不为空的数的个数。

时间复杂度大概是$O(q(n^2+m))$，其中$m$为数据范围，一定会TLE的。

改进做法1（依然暴力）

考虑到优化，在记录每次枚举区间的时候，记录下不同数的个数，就剩下了最后枚举数据范围的步骤，时间复杂度变成$O(n^2q)$

但是依然会TLE

改进做法2（离线力）

考虑离线，把所有操作都读入。

从第一个查询操作开始，每次以$O(1)$的时间复杂度拓展。

如第一个查询操作为$[l,r]$，第二个操作查询$[l-3,r+4]$，那我们就一步一步地把$l$，向左移动，每次移动的时候把拓展的数字加入cnt，更新答案，$r$同理。

形象的理解就是维护两个指针$l,r$，每次$l,r$左右移动的同时更新答案。

但是这种做法本质上还是$O(n^2q)$的（常数会小很多），所以我们需要继续优化。

改进做法3（排序大法好）

上一个做法的低效之处在于，如果第一个操作数列后面，第二个操作在最前面，$l$指针就会从末尾一路走到最前面（漂洋过海来看你？），如果出题人这样构造数据的话，复杂度就和最开始的暴力没有区别了。

考虑到排序，按照$l$排序，让$r$乱蹦跶，两个指针有序地向后窜，时间复杂度就会变成$O(qn \log n)$

依然会TLE

改进做法4（莫队算法！！！）

通过逐步的优化，我们已经摸索出了真正的莫队算法！！！

莫队算法其实就是通过某种神奇优化，把复杂度降低（莫队orz），这种排序方法就很神奇（我也不会证）

考虑分块,把数列分成$\sqrt{n}$块。

优化上一个做法，排序时，第一个关键字为左端点所在块编号，第二个关键字是右端点编号。

这种排序方式会把算法优化到$O(n\sqrt{n})$（没法再优化了！！！）

具体证明我也不会，可以看link

那么代码我们也能写出来了。

代码

const int N=1e6+10;
int cnt[N],a[N],ans=0;
struct node{
    int l,r,id,ans;
}que[N];
int T;
int Ans[N];
bool cmp(node a,node b){
    if(a.l/T==b.l/T) return a.r<b.r;//第二个关键字按照右端点编号排序
    return a.l/T<b.l/T;//第一个关键字按照左端点所在块编号排序
}
void add(int x){
    //拓展一个数
    if(!cnt[x]) ans++;//若这个数还没有过，更新答案
    cnt[x]++;
}
void del(int x){
    cnt[x]--;
    if(!cnt[x]) ans--;
}
int n,m;
int main(){
    cin>>n;
    T=sqrt(n);//分块
    for(int i=1;i<=n;i++) cin>>a[i];
    cin>>m;
    for(int i=1;i<=m;i++) cin>>que[i].l>>que[i].r,que[i].id=i;
    sort(que+1,que+1+m,cmp);//排序
    int l=1,r=0;//最开始的lr指针应该是个空区间
    for(int i=1;i<=m;i++){
        //分别拓展
        while(r<que[i].r) add(a[++r]);
        while(r>que[i].r) del(a[r--]);
        while(l>que[i].l) add(a[--l]);
        while(l<que[i].l) del(a[l++]);
        Ans[que[i].id]=ans;//记录答案
    }
    for(int i=1;i<=m;i++) cout<<Ans[i]<<endl;
}

这个代码其实就是洛谷P1972 HH的项链，但由于某洛谷知名管理员加强了数据，这题莫队就过不去了（亲测莫队能卡到48，听说有人卡到了92）。

奇偶性优化

如果$l$在奇数块，就按照$r$顺序排序，否则按照$r$逆序排序。

inline bool cmp(Que a,Que b){
    if(a.l/T!=b.l/T) return a.l/T<b.l/T;
    if((a.l/T)&1) return a.r<b.r;
    return a.r>b.r;
}

这个优化很有用，但是一般只会在卡常的时候用到。

例题1：小B的询问

原题

解题思路

在HH的项链被卡了后，这题就算是莫队模板了。

思路：用一个$cnt$数组维护区间内数字个数，然后加减时答案增删平方，剩下就是普通莫队了。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int cnt[N],a[N],ans=0;
struct Que{
    int l,r,id;//查询结构题
}que[N];
int T,Ans[N];
bool cmp(Que a,Que b){
    if(a.l/T!=b.l/T) return a.l/T<b.l/T;//第一个关键字为左端点所在块编号
    return a.r<b.r;//第二个关键字为右端点编号
}
void add(int x){
    ans-=cnt[x]*cnt[x];
    cnt[x]++;
    ans+=cnt[x]*cnt[x];
}
void del(int x){
    ans-=cnt[x]*cnt[x];
    cnt[x]--;
    ans+=cnt[x]*cnt[x];
}
int n,m,k;
int main(){
    cin>>n>>m>>k;
    T=sqrt(n);
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++) cin>>que[i].l>>que[i].r,que[i].id=i;//离线读入询问
    sort(que+1,que+1+m,cmp);//先排序
    int l=1,r=0;//起始lr指针设为一个空区间
    for(int i=1;i<=m;i++){
        //莫队算法
        while(r<que[i].r) add(a[++r]);
        while(r>que[i].r) del(a[r--]);
        while(l>que[i].l) add(a[--l]);
        while(l<que[i].l) del(a[l++]);
        Ans[que[i].id]=ans;//记录答案
    }
    for(int i=1;i<=m;i++) cout<<Ans[i]<<endl;
}

带修莫队

带修改的莫队就是在莫队的基础上多了一个修改操作（废话）

如果说普通的莫队是从$[l_1,r_1]$转移到$[l_2,r_2]$，那带修改的莫队就是从$[l_1,r_1,t_1]$转移到$[l_2,r_2,t_2]$。

所以我们可以把修改操作也存下来，执行莫队算法的时候，先按照普通莫队的做法转移到下一个区间，然后再进行（或撤销）这两次查询之间进行的修改，就相当于转移到了目标的询问。

可以把带修莫队理解成一个多了时间的坐标轴，如图

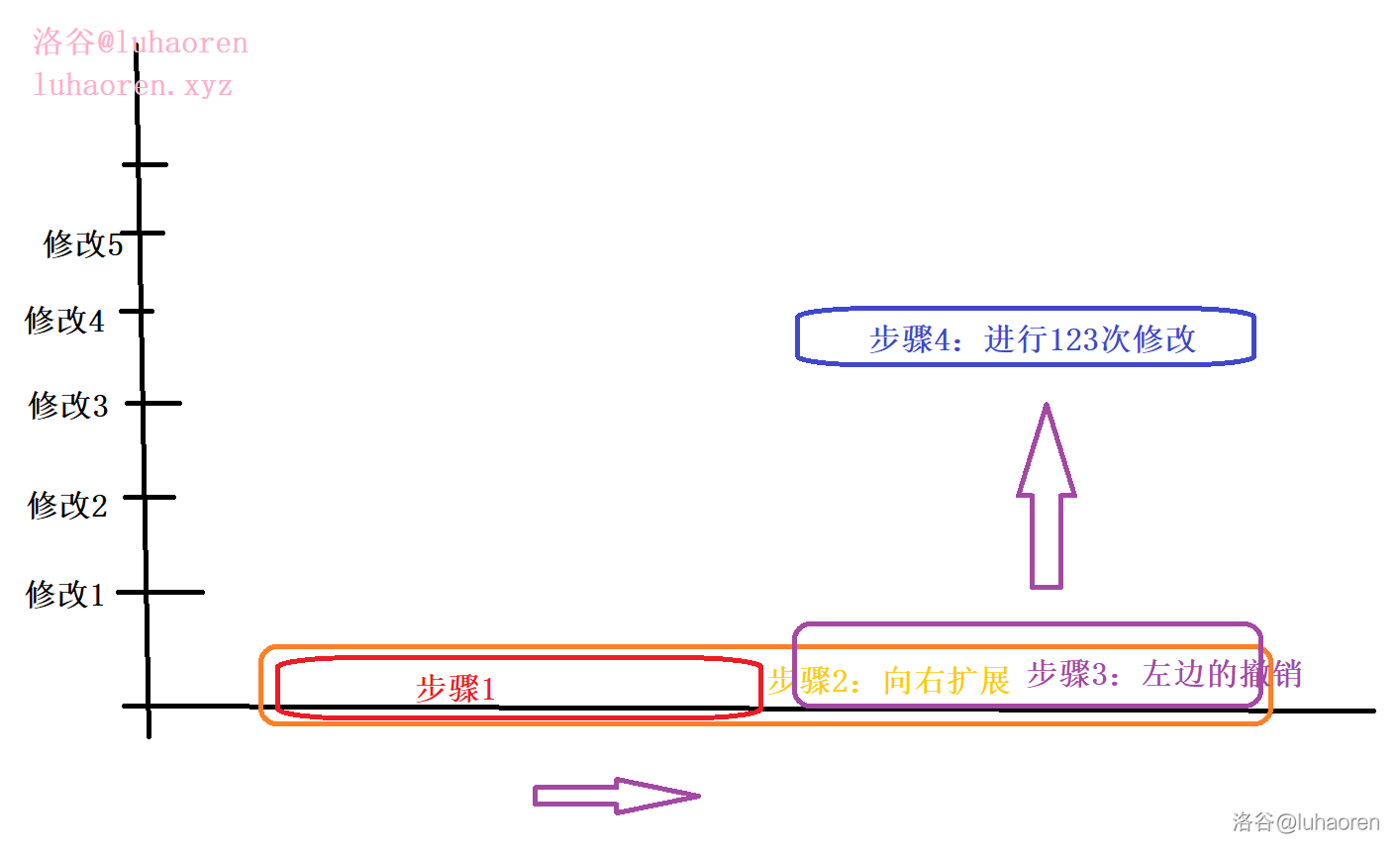
至于实现，则比较简单，排序时以左端点所在块编号为第一个关键字，右端点所在块编号为第二个关键字，第三个关键字是时间戳（在这次查询前右多少次修改）。

普通莫队维护两个指针$l,r$，带修莫队多维护一个指针$t$即可。

另外分块时不能以$\sqrt{n}$分了，带修莫队一般一块$n^{\frac{2}{3}}$，分成$n^{\frac{1}{3}}$块，复杂度为$O(n^{\frac{3}{5}})$（不会证明，可以看oiwiki）

例题2：数颜色

原题

带修莫队模板题。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int T;
struct Que{
    int l,r,id,tim;
}que[N];
int as[N];
bool cmp(Que a,Que b){
    if(a.l/T==b.l/T){
        if(a.r/T==b.r/T) return a.tim<b.tim;
        return a.r/T<b.r/T;
    }
    return a.l/T<b.l/T;
}
struct Upd{
    int p,col;
}upd[N];
int cnt[N],ans=0,a[N];
void add(int x){
    if(!cnt[x]) ans++;
    cnt[x]++;
}
void del(int x){
    cnt[x]--;
    if(!cnt[x]) ans--;
}
int n,m,iq=0,ic=0;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=m;i++){
        char opt;
        int l,r;
        cin>>opt>>l>>r;
        if(opt=='Q') que[++iq]={l,r,iq,ic};
        else upd[++ic]={l,r};
    }
    T=pow(n,0.666);//即n^2/3
    sort(que+1,que+1+iq,cmp);//排序
    int l=1,r=0,now=0;//三个指针
    for(int i=1;i<=m;i++){
        //这部分和普通莫队差不多
        while(l<que[i].l) del(a[l++]);
        while(l>que[i].l) add(a[--l]);
        while(r>que[i].r) del(a[r--]);
        while(r<que[i].r) add(a[++r]);
        //转移到新询问的时间戳
        while(now<que[i].tim){
            ++now;
            int p=upd[now].p,c=upd[now].col;
            if(l<=p&&p<=r) del(a[p]),add(c);
            swap(a[p],upd[now].col);
        }
        while(now>que[i].tim){
            int p=upd[now].p,c=upd[now].col;
            if(l<=p&&p<=r)  del(a[p]),add(c);
            swap(a[p],upd[now].col);
            now--;
        }
        as[que[i].id]=ans;//记录答案
    }
    for(int i=1;i<=iq;i++) cout<<as[i]<<endl;
}