一.基本的计数原理

1.加法原理：

就是把做一件事分类做
比如从北京到上海，可以坐飞机，还可以坐高铁，还可以坐汽车，当然也可以坐11路。。。
总共的从北京到上海的方案数就是每种方案的累加和=1+1+1+1=4

2.乘法原理

就是做一件事要分步做
还是北京到上海，比如今天北京直达上海的飞机票已经卖光了（当然不可能），但可以先从北京坐飞机到南京(共2趟)，再从南京坐高铁到上海（共7趟），所以总共的从北京到上海的方案数就是2*7=14种

二.排列组合的公式

1.排列数：

有n个人选m个人出来排队，考虑顺序
第一个人有m种选择，第二个人有m-1种选择（以为第一个位置已经有一个人了），第三个人m-2种.....最后一个位置只有n-m种选择，根据乘法原理：就是把这n-m+1种方案乘起来.
这可以写成$$n\times{(n-1)}\times{(n-2)}\times{…}\times{(n-m)}$$
又因为我们把$$n\times{(n-1)}\times{(n-2)}\times{…}\times1=n!$$
所以排列的公式可以记作：
$$P_n^m=\frac{n!}{(n-m)!}$$

2.组合数

就是有n个人选m个人出来排队，不考虑顺序
这是基于排列数的因为不需要考虑顺序所以把不需要的除掉就好了
所以组合数的公式就是：
$$C_n^m=\frac{P_n^m}{m!}=\frac{n!}{m!(n-m)!}$$

三.排列组合的应用

逐分法

就是用基本的计数原理来解决实际问题
问：现在有12位警察，要分到3个路口每个路口4个人有多少种方案
解：第一个路口有C(12,4)种选法，因为第一个路口已经用去了4位警察，所以第二个路口就只有C(8,4)种了，第三个也只有c(4,4)种了，根据乘法原理就可以得出总共的方案数就是$${C_{12}^4}\times{C_8^4}\times{C_4^4}$$

总结：这道题就是挨个路口依次考虑，分完第一个路口再分第二个，这种逐一分配的模型就是逐分法

插板法

是解决分组问题的利器
比如12个人分组，分4组一共用多少种分法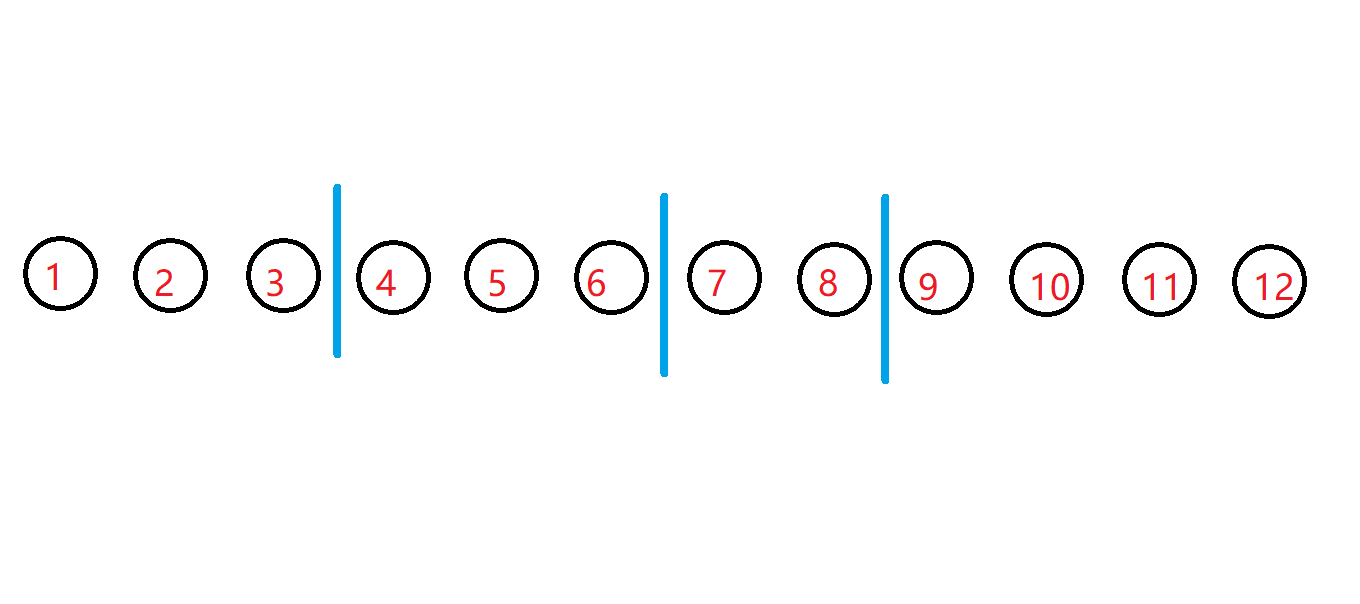
因为要分4组所以需要3个隔板，有11个空可以放隔板
因为只要隔板的位置确定了，那么整个分组的过程就确定了，所以只需要看看隔板放哪的所用情况了
每个隔板的形态都是一样的，因为每个组内成员也是可以调换位置的，所以这是一个组合问题
答案就是$$C_{11}^3$$

捆绑法

是解决相邻问题的利器
比如说这道题
现有8个人排队，甲同学和乙同学一定相邻的方案总数
可以先把甲乙捆绑让他们成为一个人，再做计算，现在一共有7个人排队，方案是7!但是甲乙是两个人，所以再用7!×2就是最后的结果
但如果是甲乙丙必须相邻的话这就有三个人了，所以最后再给这三个人排队也就是3!,所以最终答案就是7!×3!

插空法(特殊的插板法)