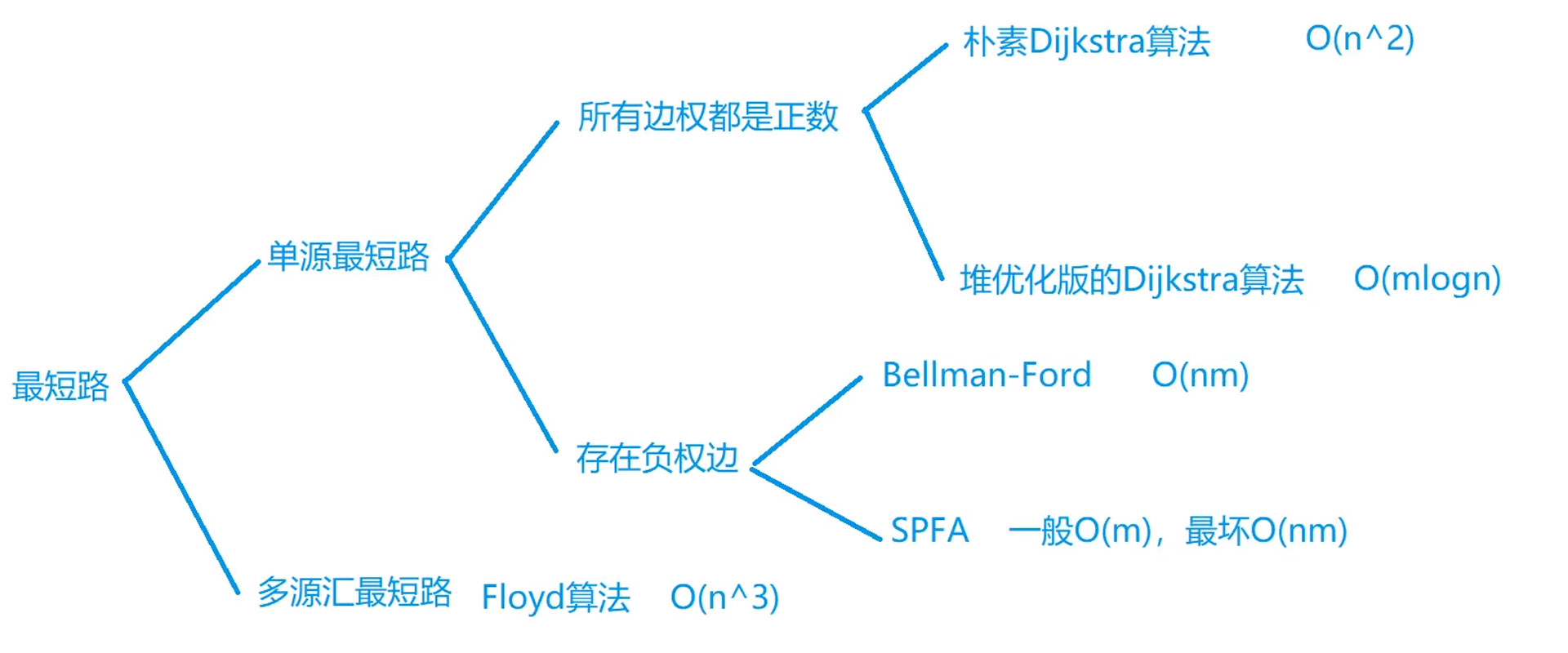
)

朴素Dijkstra算法：o(n^2)稀疏图

每次选出一个最小的边o(n)并标记，用最小的边去更新其他边，反复循环n-1次

堆优化版的Dijkstra算法:o(mlogn)稠密图

用堆存储，每次选出一个最小边的时间复杂度变为o(1)，用最小的边去更新其他边，反复循环n-1次。
ps：只有当该节点被更新了他才有可能会更新其他节点。

Bellman-Ford:o(nm)

每次遍历所有边并更新距离，遍历k遍。意义：求最短路不超过k条边的最短距离

SPFA：一般o(m),最坏o(nm)

类似于堆优化Dijkstra，用被更新的节点距离去更新其他节点，将被更新的节点存入队列，循环直至队空。

Floyd：o(n^3)

动态规划三层循环

void floyd()
{
    for(int k=1;k<=n;k++)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=n;j++)
            {
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }
}