前言

本来想写一篇计算几何的博客，没想到写不完了，那就写完向量吧

向量

有大小有方向的量。

向量可以理解为空间中的箭头，自一点出发，指向另一点，在数学中，向量的起始点一般是坐标原点。

因此向量可以用一个点表示（从原点指向那个点的向量）

如$(3,5)$表示从$(0,0)$起始，指向$(3,5)$的一个箭头。

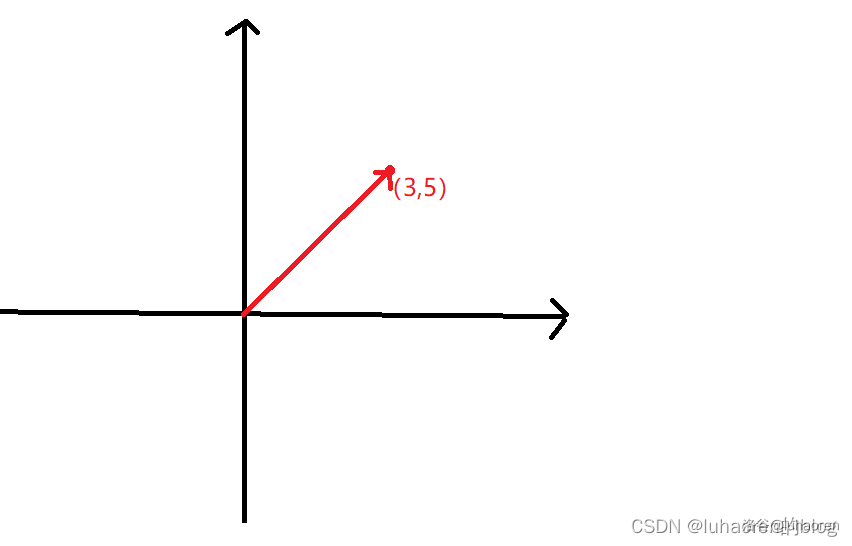
向量也可以理解为一个点的位移，如上图的向量即可理解为从$(0,0)$移动到$(3,5)$

在OI中，向量一般用一个点$(x,y)$表示，方便进行叉积等计算。

struct Vec{
    double x,y;//向量结构体
};

向量的模长

刚刚说过向量是一条箭头，模长就是箭头的长度。

若$A(x,y)$，则$|A|=\sqrt{x^2+y^2}$

struct Vec{
    double x,y;//向量结构体
    double len(){
        //返回模长
        return sqrt(x*x+y*y);
    }
};

向量的加法

如有两个向量$A$和$B$，分别表示从$(0,0)$移至$(1,2)$和从$(0,0)$移至$(3,1)$。

那么$A+B$表示什么呢？

表示先从$(0,0)$位移至$(1,2)$，再以$(1,2)$为坐标原点，移动到$(3,1)$（在新的坐标系里就是$(4,3)$），而这个过程中的位移是$(4,3)$。

向量的加法放到图像上就是把$B$平移到$A$上面，得到的那个点就是向量$A+B$的终点。

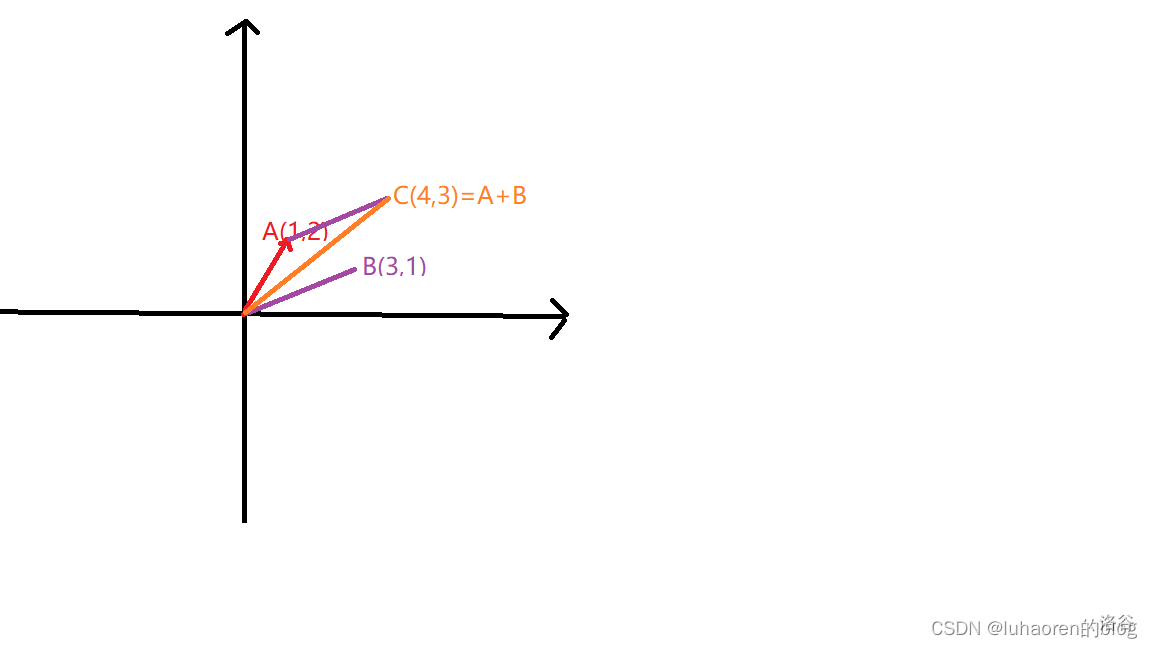
若向量$A(x_1,x_2)$，向量$B(x_2,y_2)$，则$A+B$为$(x_1+x_2,y_1+y_2)$。

Vec operator+(Vec a,Vec b){
    //向量加法
    return {a.x+b.x,a.y+b.y};
}

相反向量

如果我们有一个向量$A(x_1,x_2)$

那它的相反向量就是$-A(-x_1,-x_2)$

在图像上，就是把向量$A$的箭头方向取反。

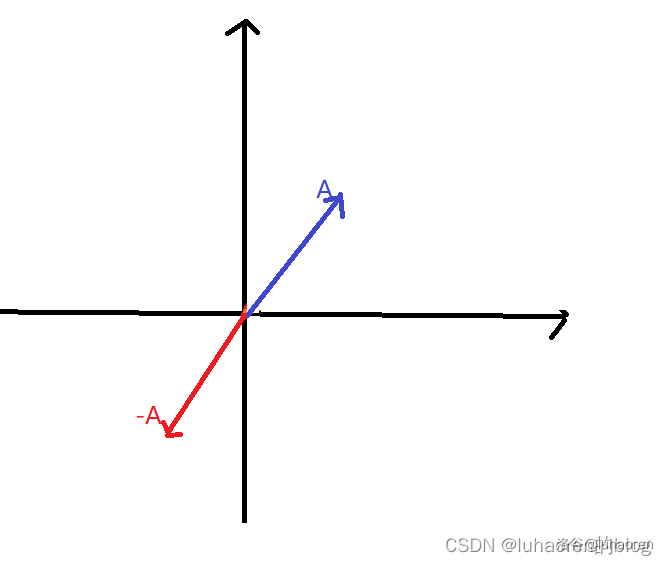
$A+(-A)=0$，两个相反向量相加结果得0，这是显然的。

向量的减法

在了解了相反向量后，向量的减法就变得很好理解。

如$A-B$，实际上就是$A+(-B)$，即A加上B的相反向量。

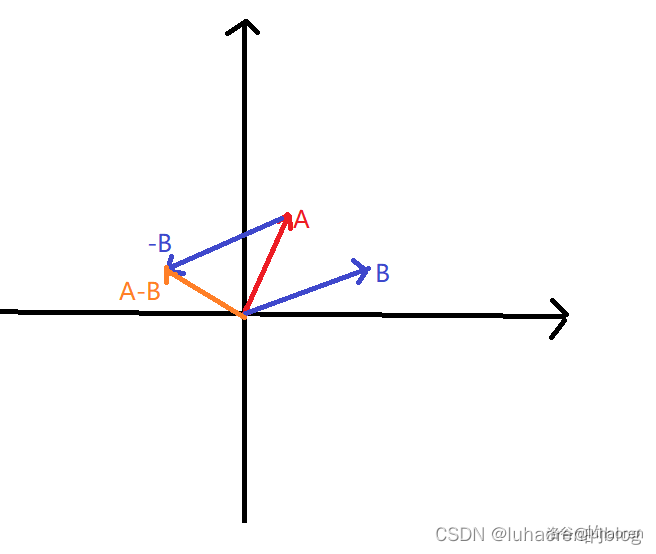
$A(x_1,y_1)-B(x_2,y_2)=C(x_1-x_2,y_1-y_2)$

Vec operator-(Vec a,Vec b){
    //向量减法
    return {a.x-b.x,a.y-b.y};
}

向量的点积

定义为
$$A\cdot B=|A|\cdot |B|\cos\langle a,b \rangle$$

即两向量模长相乘再乘上夹角的$\cos$值。

向量点积也可以写作$A\cdot B=x_A\cdot x_B+y_A\cdot y_B$

我们可以通过这个性质得到一些东西（因为程序中向量用点表示，而点积与夹角有关，所以可以求出关于夹角的一些问题）

double operator*(Vec a,Vec b){
    //向量点积
    return {a.x*b.x,a.y*b.y};
}

可以通过点积求出两向量夹角

return acos(a*b/(a.len()*b.len()));

向量的叉积

在线性代数里，向量可以写作一个矩阵$\begin{bmatrix} x_1\\\ y_1 \end{bmatrix}$

而两个向量的乘积，就是两个向量组合到一起的行列式

$$\begin{bmatrix} x_1\\\ y_1 \end{bmatrix} \cdot \begin{bmatrix} x_2\\\ y_2 \end{bmatrix}=\begin{bmatrix} x_1&x_2 \\\ y_1&y_2 \end{bmatrix}=x_1y_2-y_1x_2$$

向量叉积的几何意义是，两个向量围成的平行四边形面积

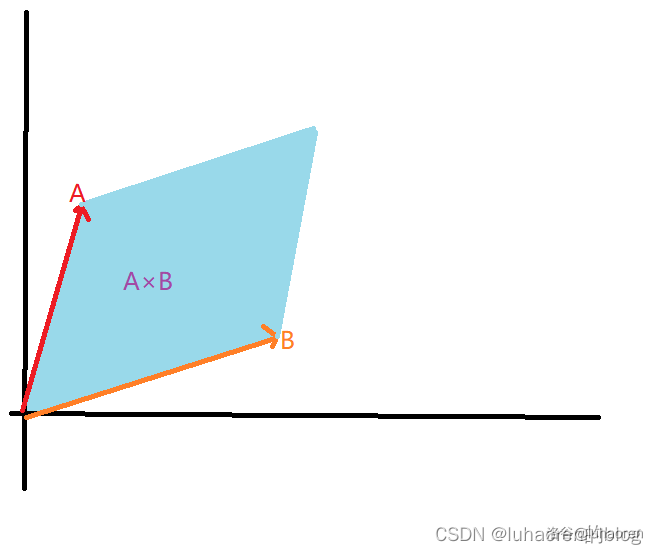
证明方法很简单，割补一下就出来了

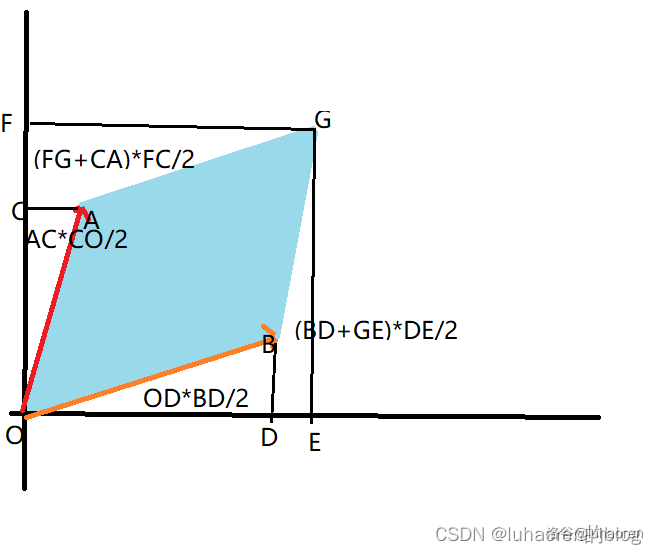
叉积的结果可能是负数，若$A\cdot B=0$ ，则向量$A,B$共线，若$>0$，则说明从$A$转到$B$是逆时
针（$B$转到$A$是顺时针），若$<0$，则说明从$A$转到$B$是顺时针（从$B$转到$A$是逆时针）

习题

求任意多边形的面积

按一定的顺序（顺、逆时针）给出一个多边形的各顶点坐标，求该多边形的面积。

思路

由于给出的坐标有顺序，我们可以相邻两个点，求两个点夹出的三角形面积。

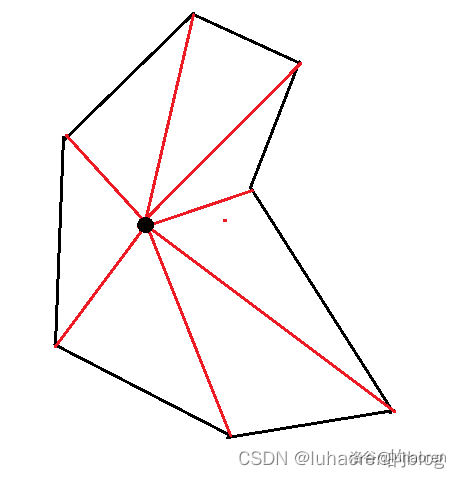
这个三角形面积就是那两个点代表向量所成的叉积的一半。

这样就很好求。

代码

#include <bits/stdc++.h>
using namespace std;
typedef double db;
const int N=110;
struct Point{
    db x,y;
    db operator*(Point b){
        //叉积
        return x*b.y-y*b.x;
    }
}p[N];
int n;
int main(){
    cin>>n; 
    db s=0;
    for(int i=1;i<=n;i++) cin>>p[i].x>>p[i].y;
    for(int i=1;i<n;i++) s+=p[i]*p[i+1]/2;
    s+=p[n]*p[1]/2;
    printf("%.1lf",s);
}