T1
题目描述
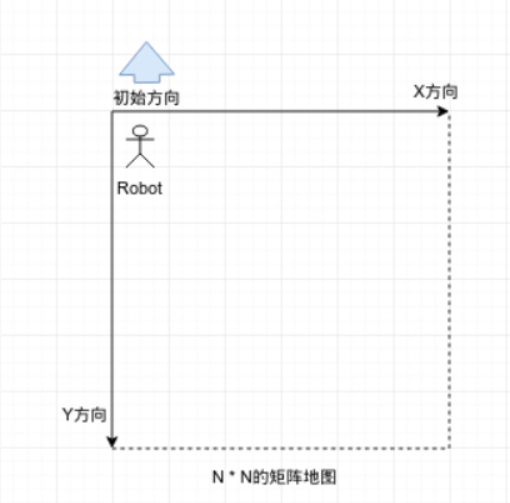
在一个$N \times N$的矩阵上有一个机器人,机器人只能接收如下几个指令:(1)L表示当前朝向向左旋转90度;(2)R表示当前朝向向右旋转90度;(3)G X表示向当前朝向前进X步,如果前方在矩阵外则会停止运动;(4)P表示汇报当前所在的坐标$(x, y)$。矩阵示意图如下,左上角坐标为$(0, 0)$,右下角坐标为$(N, N)$,一开始机器人位于左上角,面朝Y轴负方向
输入描述
第一行输入为$T$,表示一共有$T$组测试样例
每组测试样例
接下来一行有两个数字$n m$,表示地图大小为$n \times n$,机器人要执行$m$个指令
随后$m$行,每行表示一个指令
$T \leq 20$
$1 \leq n, m \leq 1000$
$0 \leq X \leq 10^9$
输出描述
对于每组测试样例,先输出一行“Case #%d:”表示第几组测试
接下来若干行,每行表示机器人执行了一次P指令汇报的坐标
示例1
样例输入
1
5 8
L
R
G 10
P
R
R
G 10
P
样例输出
Case #1:
0 0
0 4
算法
(模拟) $O(T \times m)$
- 方向为上右下左
- 注意出界
时间复杂度
T组数据,每组会进行m次操作,每次操作都是$O(1)$的,因此总时间复杂度为$O(T \times m)$
C++ 代码
#include <bits/stdc++.h>
using namespace std;
int T, n, m;
int x, y, u;
int dx[4] = {0, 1, 0, -1}, dy[4] = {-1, 0, 1, -1};
int main() {
cin >> T;
for (int C = 1; C <= T; C ++ ) {
printf("Case #%d:\n", C);
cin >> n >> m;
x = 0, y = 0, u = 0;
char op;
while (m -- ) {
cin >> op;
if (op == 'L') {
u -- ;
if (u < 0) u += n;
} else if (op == 'R') {
u = (u + 1) % n;
} else if (op == 'G') {
int c; cin >> c;
x += dx[u] * c, y += dy[u] * c;
x = max(0, x), x = min(x, n - 1);
y = max(0, y), y = min(y, n - 1);
} else {
cout << x << ' ' << y << endl;
}
}
}
return 0;
}
T2
题目描述
有一串多彩的珠子(其中最多9种颜色)。称其中最长的连续颜色相同的一串珠子为主串。为了获得一段尽量长的主串,这里最多可以修改一颗珠子的颜色。希望知道此后主串最长可以为多长。
输入描述
第一行为一个数$M$,表示之后会有$M$个用例
第二行到第$M + 1$行,每一行为一个只包含1~9的字符串,表示该用例下珠子串初始的颜色
$0 < X \leq 10^6$
输出描述
输出应当有$M$行,每行包括一个数字,为最多修改一个珠子后,最长的主串的长度。
示例1
样例输入
2
123112111
111
样例输出
6
3
算法
() $O()$
时间复杂度
C++ 代码
T3
题目描述
摩尔斯电码是一种早期的数字化通信形式,但是它不同于现代只使用0和1两种状态的二进制代码,包括了点、划、字符内部的停顿、字符之间的停顿、单词之间的停顿五种代码。而不同的点和划的组合,对应了不同的数字和字母。具体对应关系如下:

我们希望只用0和1来表示这五种代码,具体表示关系如下:
(1)点(.):1
(2)划(-):111
(3)字符内部的停顿(在点和划之间):0
(4)字符之间的停顿:000
(5)单词之间的停顿:0000000
现在有一段01表示的莫尔斯电码,需要你翻译出原始的数字和大写字母。
输入描述
输入为一行01字符串,表示了一段摩尔斯电码。
01字符串长度不超过20000。
输出描述
输出一行翻译结果的字符串。字符串由数字、大写字母和空格组成。
示例1
样例输入
1010100011101110111000101010000000101110111011101110001010111011101110001010101110111
样例输出
SOS 123
算法
() $O()$
时间复杂度
C++ 代码
T4
题目描述
现在你有一个由整数组成的数组,请找出数组中所有$x ^ 2 < z ^ 2 < y ^ 2$的偏序三元组$(x, y, z)$(即在数组中的顺序为$x$在前,$y$在中间,$z$在后),并输出它们的数量。$x, y, z$三者中只要存在一个数字的在数组中的位置不同,就视为不同的三元组
输入描述
每组数据第一行:$N$
每组数据第二行:$N$个绝对值小于$10 ^ 5$的数字
$1 \leq N \leq 10 ^ 5$
输出描述
一个数字,表示要求的偏序三元组的数量
由于数字可能很大,请把答案对$1e^8 + 7$取模
示例1
样例输入
5
3 5 2 4 1
样例输出
1
说明
只有3 5 4这一组符合要求
算法
(树状数组) $O(nlog(n))$
- 先把所有负数转成正数,题意是求形如“132”的数对的个数
- 用树状数组计算每个数左边比它小的数的个数$l[i] = \sum_{k=1}^{i-1}[a_k < a_i]$
- 枚举2的位置$i$,假设1和3对应的数为$a_x$和$a_y$($x < y < i, a_x < a_i < a_y$)。通过计算满足$(a_x < a_i, x < i, y < i)$的减去其中$(a_y < a_i, x < y < i)$的和$(y \leq x < i)$的
C++ 代码
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10, mod = 1e8 + 7;
int n;
LL ret;
int a[N], l[N], g[N], tr[N];
int lowbit(int x) {
return x & -x;
}
void add(int x, int c) {
for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}
int sum(int x) {
int ret = 0;
for (int i = x; i; i -= lowbit(i)) ret += tr[i];
return ret;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> a[i], a[i] = abs(a[i]);
for (int i = 1; i <= n; i ++ ) {
l[i] = sum(a[i] - 1);
add(a[i], 1);
}
memset(tr, 0, sizeof tr);
for (int i = 1; i <= n; i ++ ) {
ret = (LL)(ret + l[i] * (i - 1) - l[i] * (l[i] - 1) / 2 - sum(a[i] - 1)) % mod;
add(a[i], i);
}
cout << ret;
return 0;
}


第二题应该可以O(N), 前后各扫一遍, 然后再合并
这里我没写
else,其他跟你一样,可能就这错了在等一个大佬出第四题,感觉应该是O(nlogn), 因为N <= 1e5, 二分,树状数组,线段树, 但是就是没整出来
这是我最惨的一次笔试了,全程在调第二题和第三题