$\LARGE{引言}$

本文会以例题 玩具装箱 来介绍斜率 dp。

$\LARGE{分析}$

为了方便，记 $L:=L+1, s_i = \sum_{j=1}^i c_j + 1$

列出方程 $$f_i = \min_{j=0}^{i-1} f_j + (s_i - s_j - L) ^ 2$$

展开 $$f_i = \min_{j=0}^{i-1} f_j + s_i ^ 2 - 2s_i(s_j+L) + (s_j+L)^2$$

若对与 $i$ ，有 $0\leq j_1 < j_2 < i$ ，要满足 $j2$ 比 $j1$ 更优，则

$$f_{j_1} - 2s_i(s_{j_1}+L)+(s_{j_1} + L)^2 \ge f_{j2} - 2s_i(s_{j_2} + L) + (s_{j_2} + L)^2$$

$$2s_i(s_{j_2}-s{j_1}) \ge f_{j2} + (s_{j_2}+L)^2 - (f_{j_1}+(s_{j_1}+L)^2)$$

$$\because s_{j_2} - s_{j_1} \ge 0$$

$$2s_i \ge \frac{f_{j2} + (s_{j_2}+L)^2 - (f_{j_1}+(s_{j_1}+L)^2)}{s_{j_2}-s{j_1}}$$

若设 $x_j = s_j, y_j = f_j + (s_j + L)^2$

让 $j$ 在直角坐标系上表示为点 $(x_j, y_j)$ 。

那么只需要让

$$2s_i \ge \frac{y_{j_2} - y_{j_1}}{x_{j_2}-x_{j_1}}$$

即大于等于 $j_1$ 和 $j_2$ 的斜率。

若有 $i$ ， $j$ ， $k$

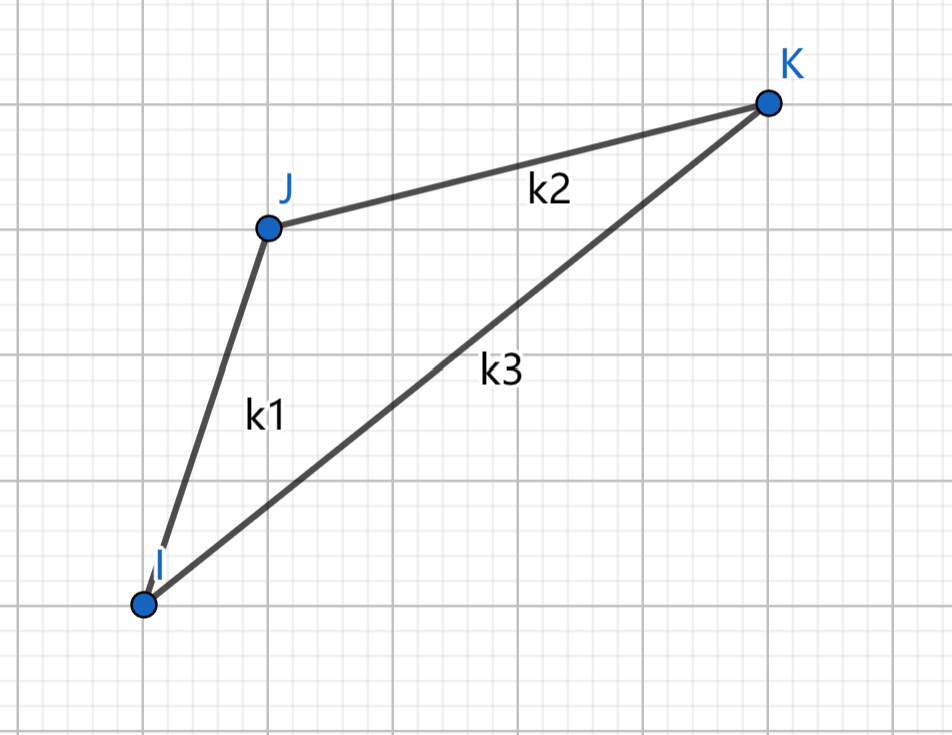
可以看出 $k2 < k3 < k1$

若有 $2s_i \ge k1$ 那么一定满足 $2s_i\ge k2$ 所以一定会选择 $k$ 而不是 $j$ ，

所以 $j$ 就可以删去，删去所有 $j$ 后形成斜率不降的下凸包。

由于此题满足 $s$ 单调递增，所以可以不用在凸包上二分，可以用单调队列维护。

$\LARGE{实现}$

#include <bits/stdc++.h>
#define LL long long
using namespace std;

const int N = 5e4 + 10;
int n, L;
int q[N];
LL c[N], f[N];

double slope(int a, int b) {
    LL y = f[b] - f[a] + (c[b] + L) * (c[b] + L) - (c[a] + L) * (c[a] + L);
    LL x = c[b] - c[a];
    return y * 1.0 / x;
}

int main() {
    scanf("%d%d", &n, &L);
    L ++ ;
    for (int i = 1; i <= n; i ++ ) {
        scanf("%lld", &c[i]);
        c[i] += c[i - 1] + 1;
    }
    int hh = 0, tt = 0;
    for (int i = 1; i <= n; i ++ ) {
        while (hh < tt && slope(q[hh], q[hh + 1]) <= 2 * c[i]) hh ++ ;
        f[i] = f[q[hh]] + 1ll * (c[i] - c[q[hh]] - L) * (c[i] - c[q[hh]] - L);
        while (hh < tt && slope(q[tt], i) < slope(q[tt - 1], q[tt])) tt -- ;
        q[++ tt] = i;
    }
    printf("%lld", f[n]);
    return 0;
}