介绍

manacher算法，一种充斥着极简暴力美学的算法，俗称马拉车算法，是为了解决一个字符串内最长回文字串的一个算法，该算法时间复杂度为$O(N)$（$N$为字符串长度）。

一个故事

有一天，小L在路上走着走着，发现脚下飘来一张纸片，纸片上赫然写着一道题！！原来是有人求助，赏金200块。小L出于自己的好奇心（确定不是因为那200块???），想试着做一做这个题，题目如下：
-----------不怎么华丽的分割线-----------------

给出一个只由小写英文字符 $\texttt a,\texttt b,\texttt c,\ldots\texttt y,\texttt z$ 组成的字符串 $S$ ,求 $S$ 中最长回文串的长度 。

字符串长度为 $n$。

小L遇见这个题，立马想出了三种方法：
1. 直接枚举起点和终点，再暴力判断，时间复杂度$O(n^3)$
2. 也是枚举起点和终点，但是用哈希做到$O(1)$判断，时间复杂度$O(n^2)$
3. 对答案进行二分，枚举起点再用哈希判断，时间复杂度$O(nlogn)$

不会哈希的看这里

正当小L准备把第3种方法写出来时，他随手瞄了一眼数据范围，结果看见一行大字：

$n \le 10^7$

他揉了揉眼睛，结果还是：

$n \le 10^7$

于是小L逐渐意识到问题的严重性，“看来这200块还真不是好拿的，那咋办呢？”。

思路历程（重点会加粗）

“回文，回文…回文有什么特殊性质吗？有啊！一个回文串是可以找到一条‘对称轴’的，但是奇数偶数分类好麻烦。。如果回文串长度全是奇数就好了。”
“得先想想有没有什么办法能让长度全是奇数呢？哦，可以在每两个字符之间插一个用来占位的字符，就用字符’#’吧，例如$\texttt a\texttt b\texttt a\texttt a\texttt b\texttt c$就可以变成$\texttt #\texttt a\texttt #\texttt b\texttt #\texttt a\texttt #\texttt a\texttt #\texttt b\texttt #\texttt c\texttt #$（看不懂的看下图）”

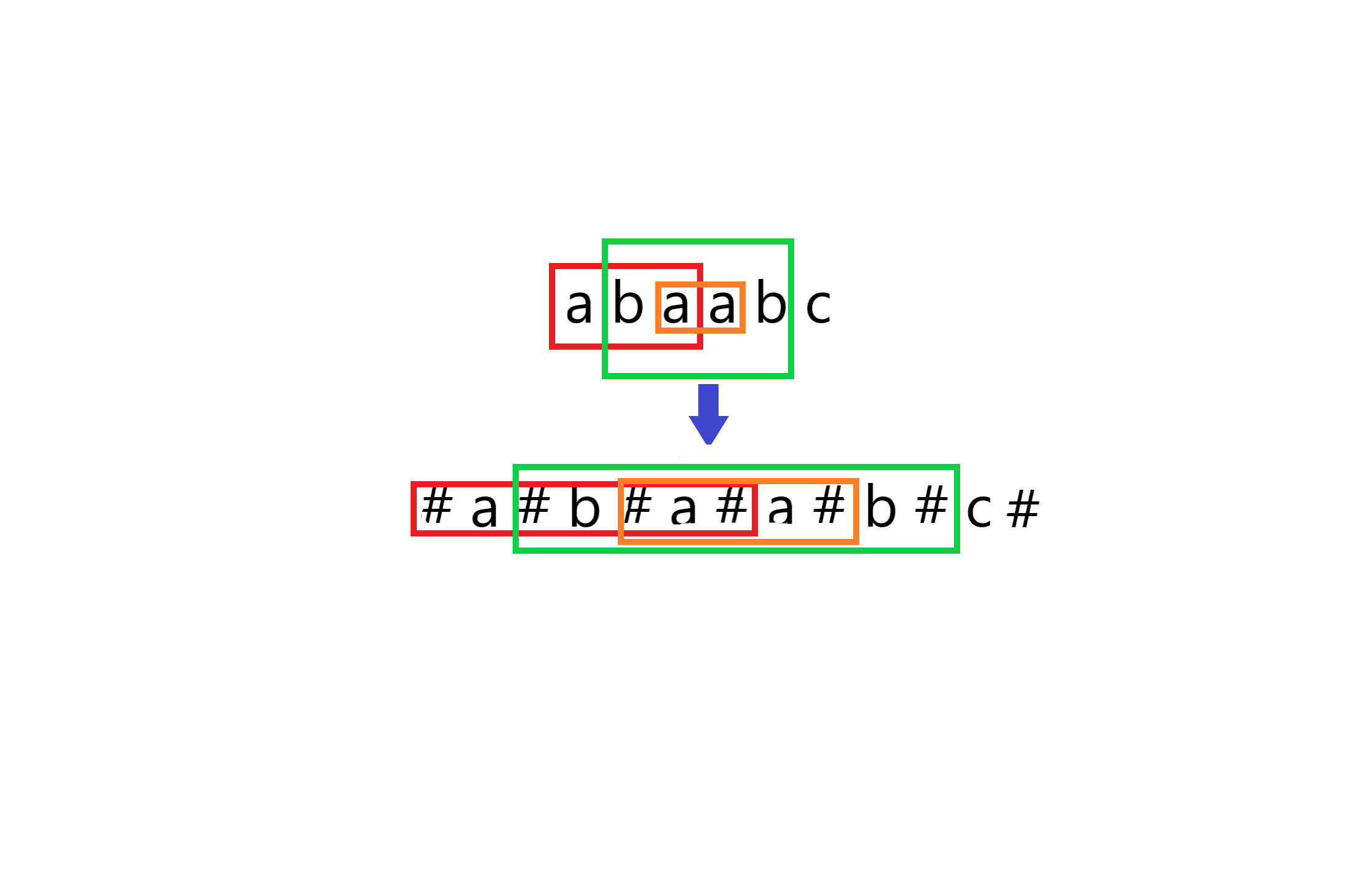
（在原串中框起来的是回文子串，在下面的串中对应的是变换之后的回文子串）
“这样一来就全是奇数了，就简单多了，但对于解题还是没有什么帮助啊。。可以把字串长度表示成转化完的串的‘半径’减一。”

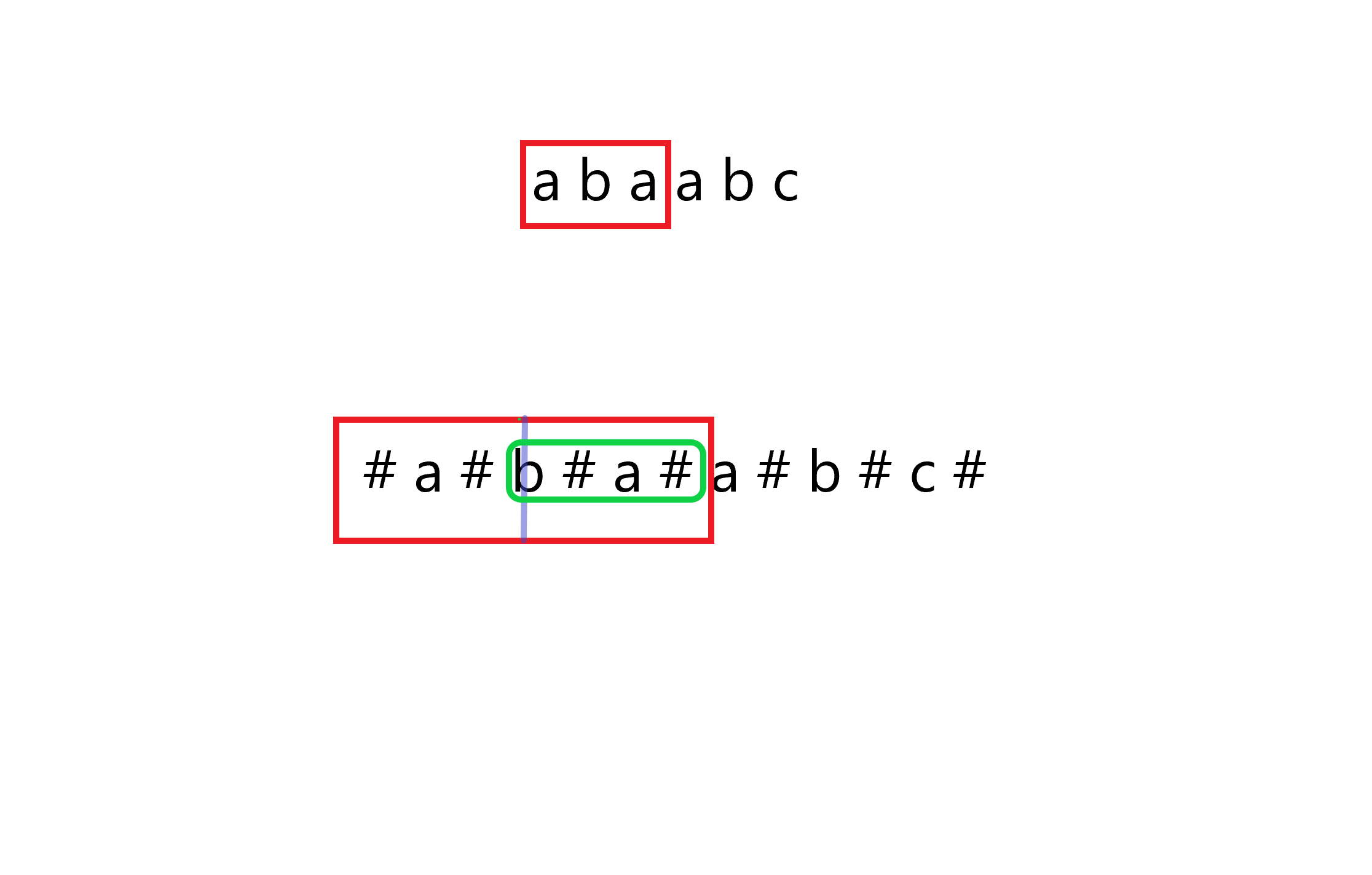
“这个半径可以用$p$数组存起来，那如何快速求出$p$数组呢？考虑用之前的$p$计算现在的$p$，设一个半径是$[l,r]$，且$l \le i$且$r$最大，若$i \le r$则$p(i) \ge \min(p(2*l-i),r-i)$（这个不难理解吧），否则$p(i) \ge 1$，接下来依次增大$p(i)$就行了，但时间复杂度呢？先把代码写出来看看吧。”

int mid,mr=0,ans=0,i;//mid和mr对应原文中的l和r
for(i=1;i<=n;++i){
    if(i<mr)p[i]=min(p[(mid<<1)-i],mr-i);else p[i]=1;
    while(st[i-p[i]]==st[i+p[i]])++p[i];//逐渐增大
    if(i+p[i]>mr){//更新
        mr=i+p[i];
        mid=i;
    }
    ans=max(ans,p[i]);//统计答案
}
return ans;

“由于$p(i)$增加的越多则$mr$增加的越多，所以整体时间复杂度是$O(N)$的。200块到手了！！！”

总结

以上就是manacher算法的思路过程，实际写时可能要再做一些处理，例如左右两端还需再加一个不同的字符，可以看代码理解。

Code（manacher模板题AcWing/Luogu）

${\color{Red} {Talk \quad is \quad cheap \quad,\quad show \quad me \quad the \quad code.}}$

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int,int> PII;
int p[22000010],n;
char st[22000010];
int manacher()
{
    int mid,mr=0,ans=0,i;
    for(i=1;i<=n;++i){
        if(i<mr)p[i]=min(p[(mid<<1)-i],mr-i);else p[i]=1;
        while(st[i-p[i]]==st[i+p[i]])++p[i];
        if(i+p[i]>mr){
            mr=i+p[i];
            mid=i;
        }
        ans=max(ans,p[i]);
    }
    return ans;
}
void write(int x)
{
    if(x>9)write(x/10);
    putchar((x%10)+'0');
}
int main()
{
    int i;
    char ch=getchar();
    st[++n]='$';
    while(~ch)st[++n]='#',st[++n]=ch,ch=getchar();
    st[++n]='#',st[++n]='^';
    write(manacher()-1);
}

来切道水题练练手吧LuoguP3501（好像可以用哈希+二分），还有双倍经验（而且还是紫的）LuoguSP15569。