建议在个人博客上看。

前言

FHQtreap绝对是平衡树里最好写，最实用的，他几乎能做所有splay或其它平衡树能做的事，还能可持久化！

这篇文章将会介绍FHQtreap的基本操作和维护区间的操作，并附上例题。

基本操作

FHQtreap的基本操作只有两个，分裂和合并。

有些读者可能会问，分裂和合并和平衡树有什么关系？

想想一下，如果要插入一个数3，在正常的平衡树里应该是找到3的位置，然后让他的$cnt$值$+1$，在FHQtreap里可不是这样，所谓插入，就是把平衡树按照3分裂成两棵树，然后把3这个数的节点合并进去。

删除呢？直接按照3分裂，然后在左子树里把3“抠出去”，再合并。

其它操作也大同小异，你会发现，大部分平衡树的操作，都可以用分裂和合并来表示，这就是FHQtreap的特点，这种思想被称为“函数式编程”。

节点结构

FHQtreap每个节点要保存的信息有权值（这个数），优先级（随机数)，子树大小，左右子树的编号。

struct node{//节点结构体
    int x,rnd,size;
    int ls,rs;
}tr[N];

注意：FHQtreap不需要存储$cnt$，它把权值相同的节点看成多个节点 。

pushup操作

也叫maintain操作，调整子树大小。

inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}

分裂

FHQtreap的分裂操作有两种，一种是通过权值分裂（小于等于$x$的分到左子树，大于$x$的分到右子树），一种是通过大小分裂（前$size$个数分到左子树，剩下的分到右子树）

如图，将一棵树按7分裂成两棵树。

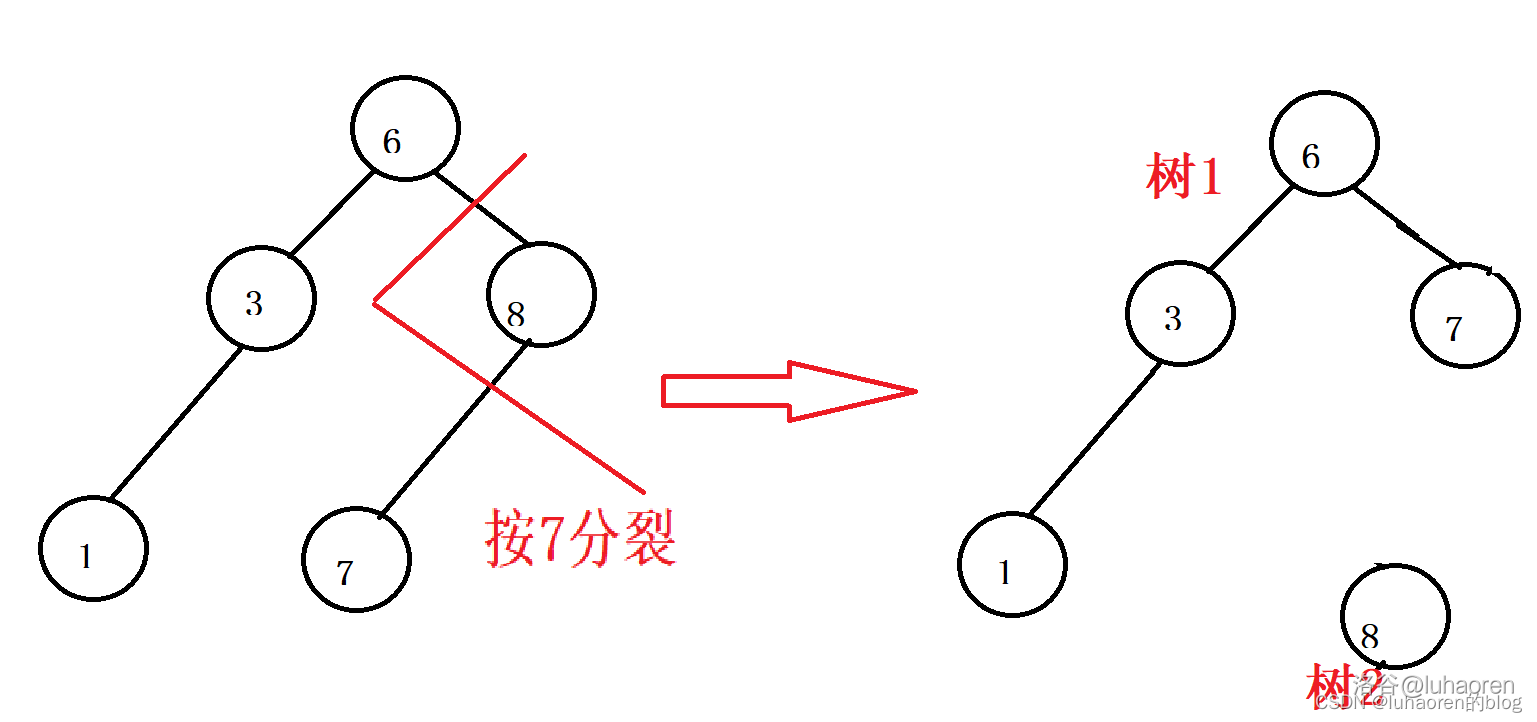
分裂后，就产生了$\{x|x\le 7\}$和$\{x|x> 7\}$两颗树。

按权值分裂代码

void split(int u,int &x,int &y,int val){//x和y用引用形式，是要分裂成的两棵树
    if(!u){
        x=y=0;//递归终止条件
        return;
    }
    if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);//当前权值小于等与要分裂的值，递归分裂右子树
    else y=u,split(tr[y].ls,x,tr[y].ls,val);//递归分裂左子树
    pushup(u);//最后别忘了pushup一下。
}

FHQtreap也可以按照大小分裂，将在区间操作的部分提到，这里给出代码。

按大小分裂代码

void split(int u,int &x,int &y,int size){
    if(!u){
        x=y=0;
        return;
    }
    if(tr[tr[u].ls].size<size) x=u,split(tr[u].rs,tr[u].rs,y,size-tr[tr[u].ls].size-1);//注意，这里传的值要减去左子树大小
    else y=u,split(tr[u].ls,x,tr[y].ls,size);
    pushup(u);
}

合并

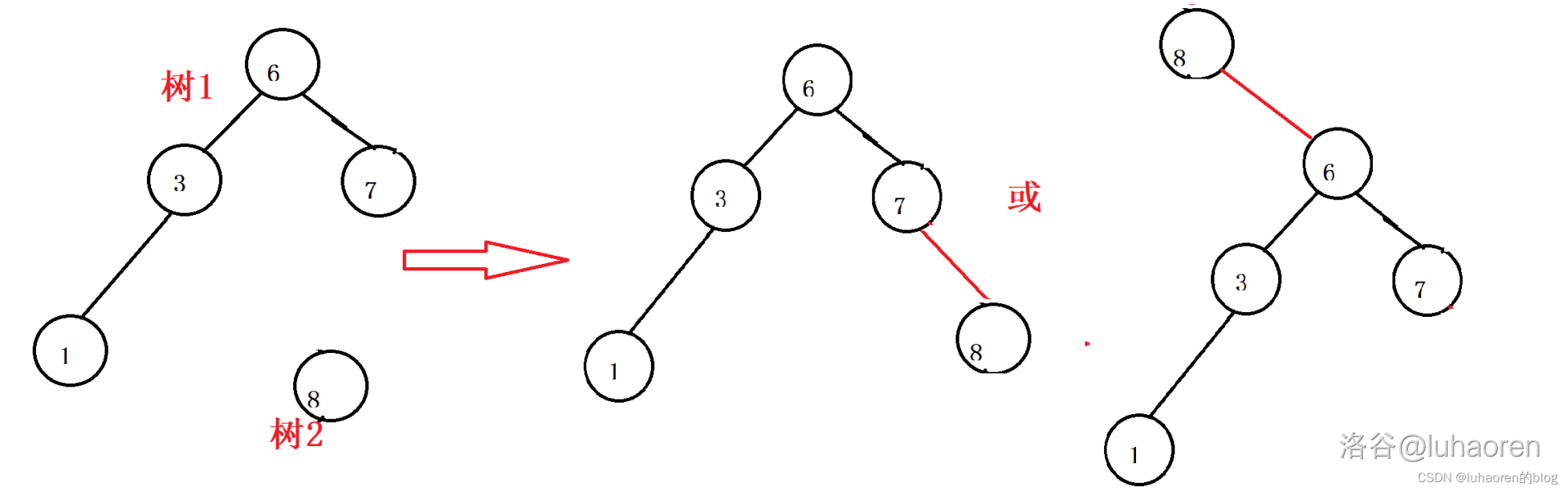
FHQtreap的合并操作很像是线段树合并，是一种启发式合并。

如图，合并操作可以有多种合并方式，这取决于每个节点所附带的优先级（随机值），使这颗树的优先级符合$heap$性质（感兴趣的可以了解一下treap的平衡方式，这里不细讲了）

合并操作代码

int merge(int x,int y){
    if(!x||!y) return x+y;
    //这个x+y实际上就是返回x和y中不为空的一个
    if(tr[x].rnd<tr[y].rnd){//通过优先级调整
        tr[x].rs=merge(tr[x].rs,y);//启发式合并
        pushup(x);//更新节点信息
        return x;//合并后的节点就变成了x
    }
    else{
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}

其它操作

学会了基本的分裂和合并操作，我们就可以做到插入，删除这些操作了。

新建节点

这个新建节点的操作大概是本人独有的，大部分oier都不会这么写，但是这么写的好处就是简短清晰（只需两行）。

int newNode(int x){
    tr[++tot]={x,rand(),1,0,0};//结构体的赋值方法，分别传入权值、优先级、大小和左右子树编号（0）
    return tot;//返回新建节点的编号
}

插入

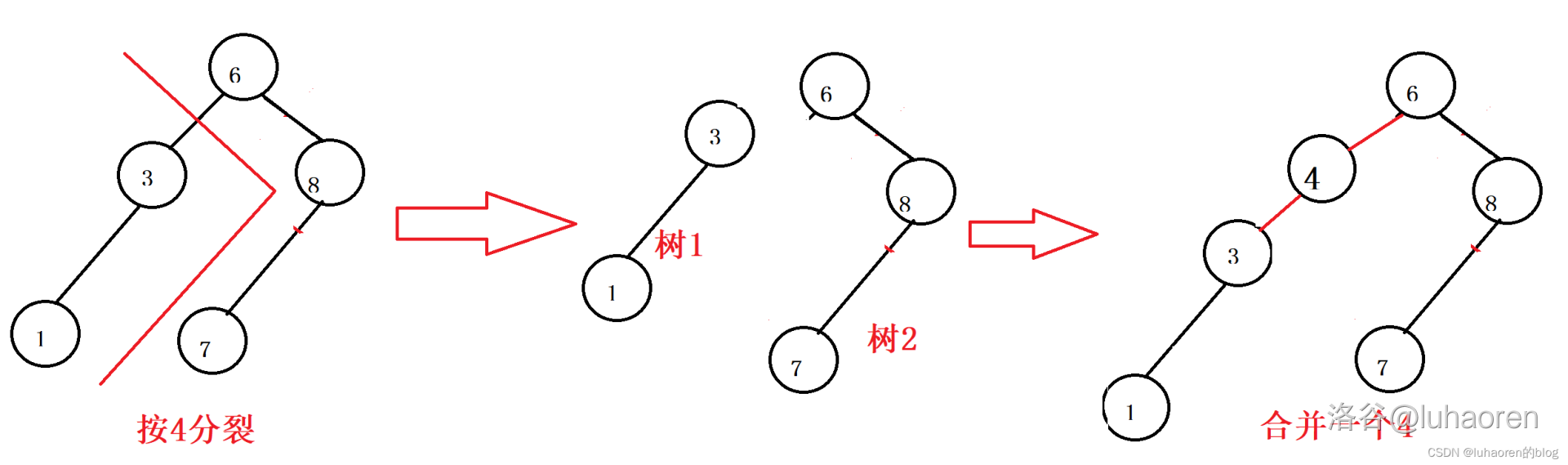
如图，若插入一个$x$，先按$x$分裂，然后新建一个节点$x$合并进去。

插入代码

void insert(int x){
    int l,r;
    split(root,l,r,x);
    root=merge(merge(l,newNode(x)),r);
}

删除

删除操作比较复杂，如图，先按$x$分裂成两颗子树（树1和树2）。

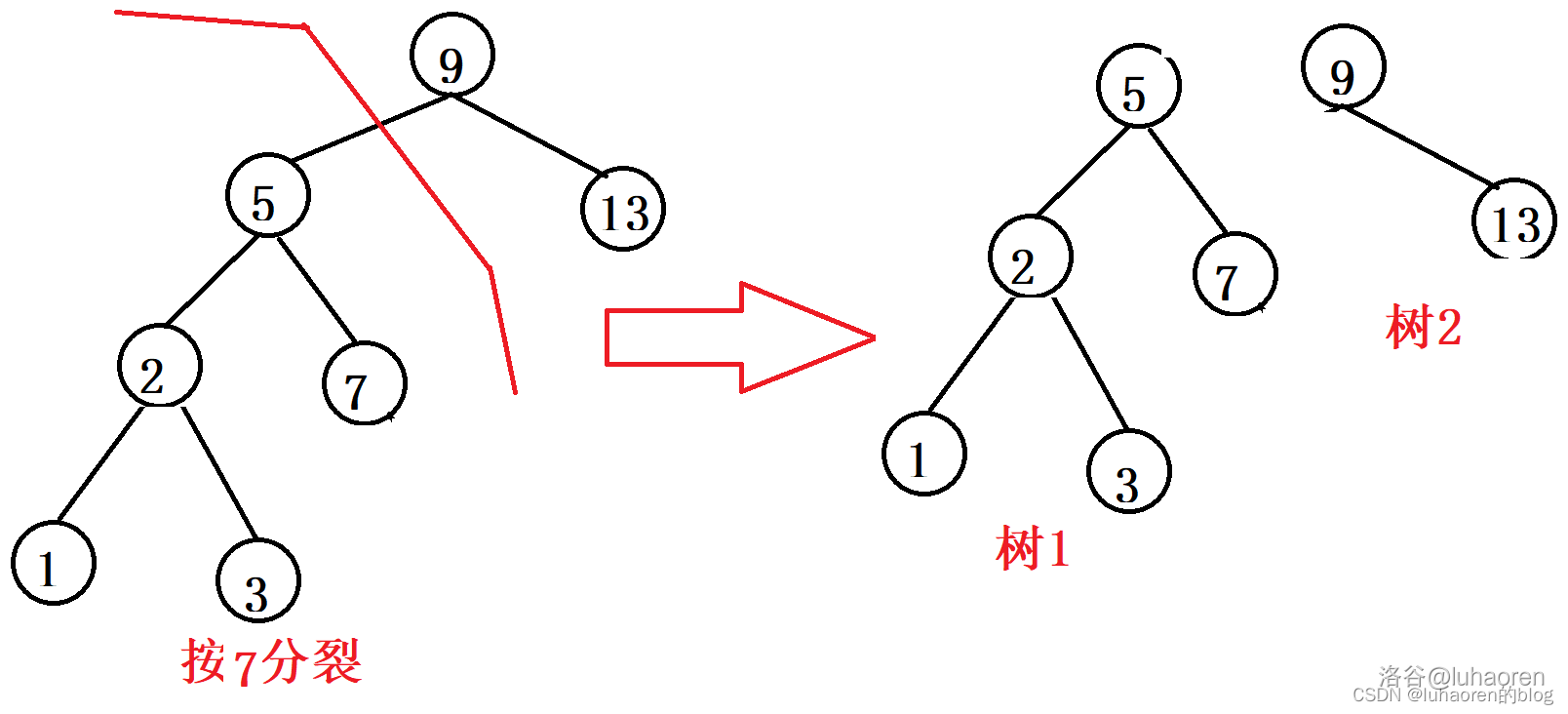
再按$x-1$分裂成两棵子树（树3和树4）。

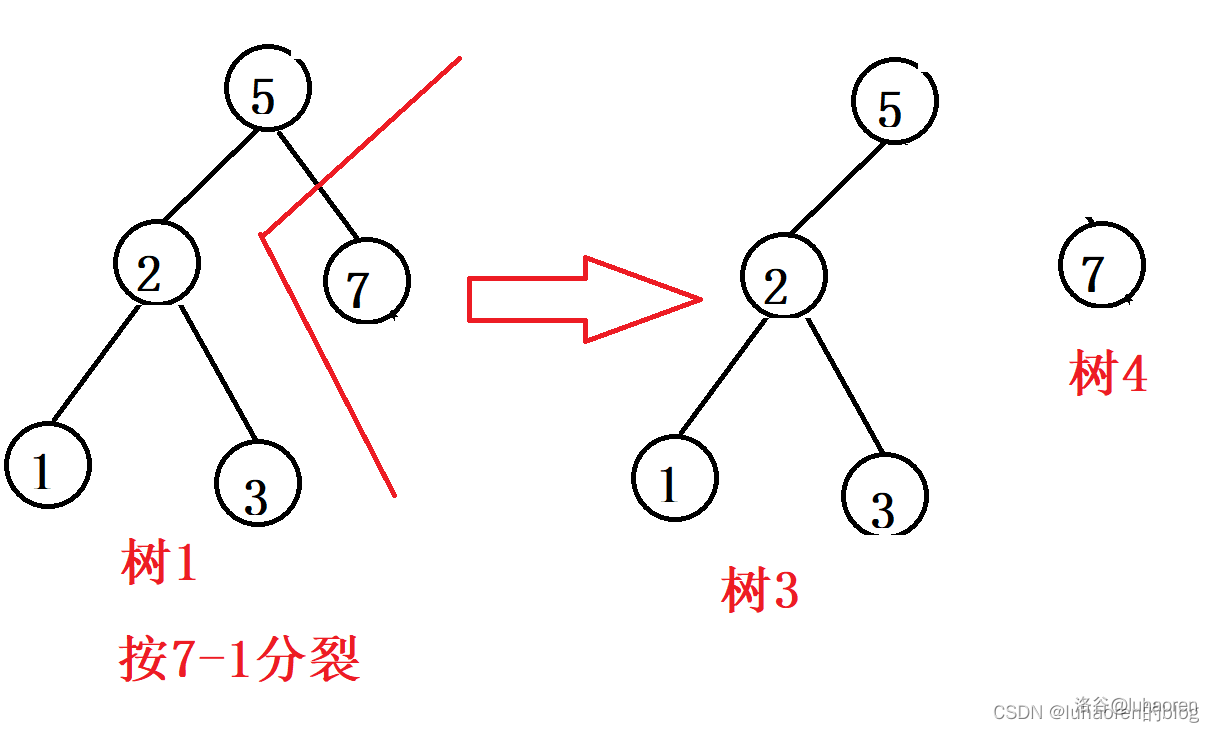
此时树4的根就是我们要找的$x$，把树4的根挑出去，然后合并树342即可。

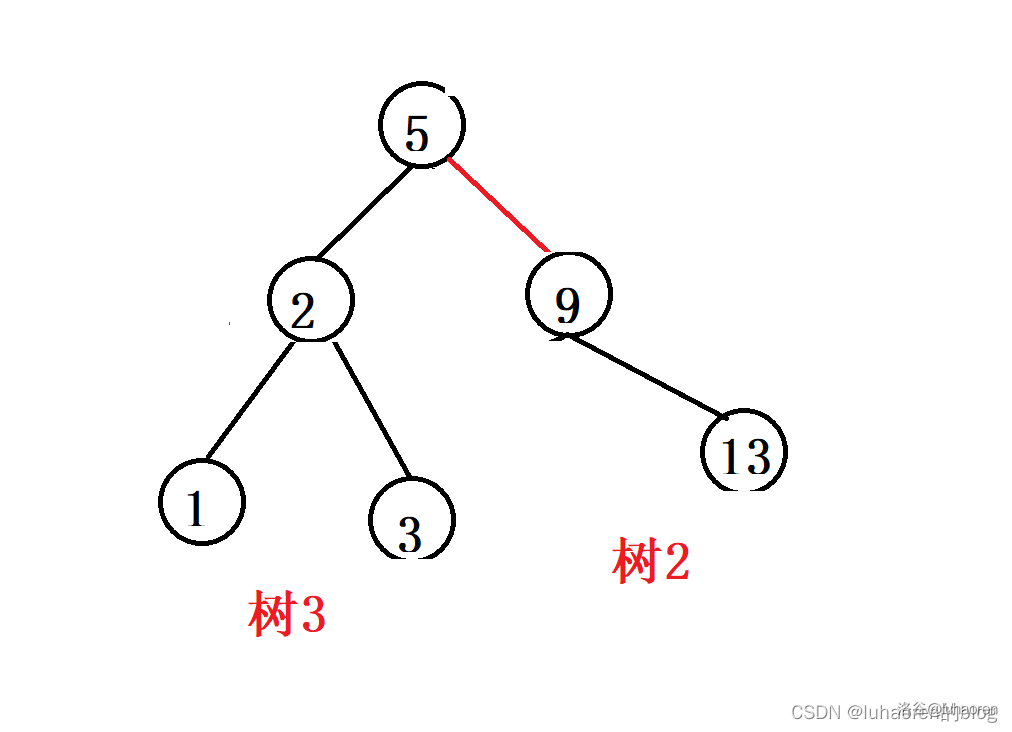
删除代码

void del(int x){
    int l,r,xx,yy;//分别代表数1234
    split(root,l,r,x);//按x分裂
    split(l,xx,yy,x-1);//按x-1分裂
    yy=merge(tr[yy].ls,tr[yy].rs);//把树4的根挑出去
    root=merge(merge(xx,yy),r);//合并
}

查询一个数的排名

排名的定义是”小于这个数的个数$+1$”。
按照定义，按$x-1$分裂，左子树的大小$+1$就是排名。

int rnk(int x){
    int l,r;
    split(root,l,r,x-1);
    int tmp=tr[l].size+1;
    root=merge(l,r);
    return tmp;
}

查询排名为k的数

这个操作无法用按权值分裂来解决，一般来说有两种写法，一种是使用按大小分裂的方法，分裂出前k个数；另一种是二分解决，这里给出后者的代码。

查询第k大代码

int kth(int u,int k){
    int p=tr[tr[u].ls].size+1;
    if(p==k) return tr[u].x;
    if(p<k) return kth(tr[u].rs,k-p);
    return kth(tr[u].ls,k);
}

前驱和后继

前驱

前驱定义为小于$x$的最大的数，按照定义，我们按$x-1$分裂，左子树最大的一个数（即$kth(l_{size})$)就是$x$的前驱。

求前驱代码

int pre(int x){
    int l,r;
    split(root,l,r,x-1);
    int tmp=kth(l,tr[l].size);
    root=merge(l,r);
    return tmp;
}

后继

同理，按照$x$分裂，右子树的最小值就是$x$的后继。

求后继代码

int nxt(int x){
    int l,r;
    split(root,l,r,x);
    int tmp=kth(r,1);
    root=merge(l,r);
    return tmp;
}

维护区间

区间操作一般由线段树维护，但是，有些问题（如区间翻转）用线段树维护就比较麻烦，那么该用什么维护呢？

平衡树。

事实上，平衡树除了可以作为”排序树“，也可以作为”区间树“，以在数列中的序号为权值建一棵平衡树（这颗平衡树的中序遍历就是原数列），就可以轻易地修改和查询一段区间的信息。

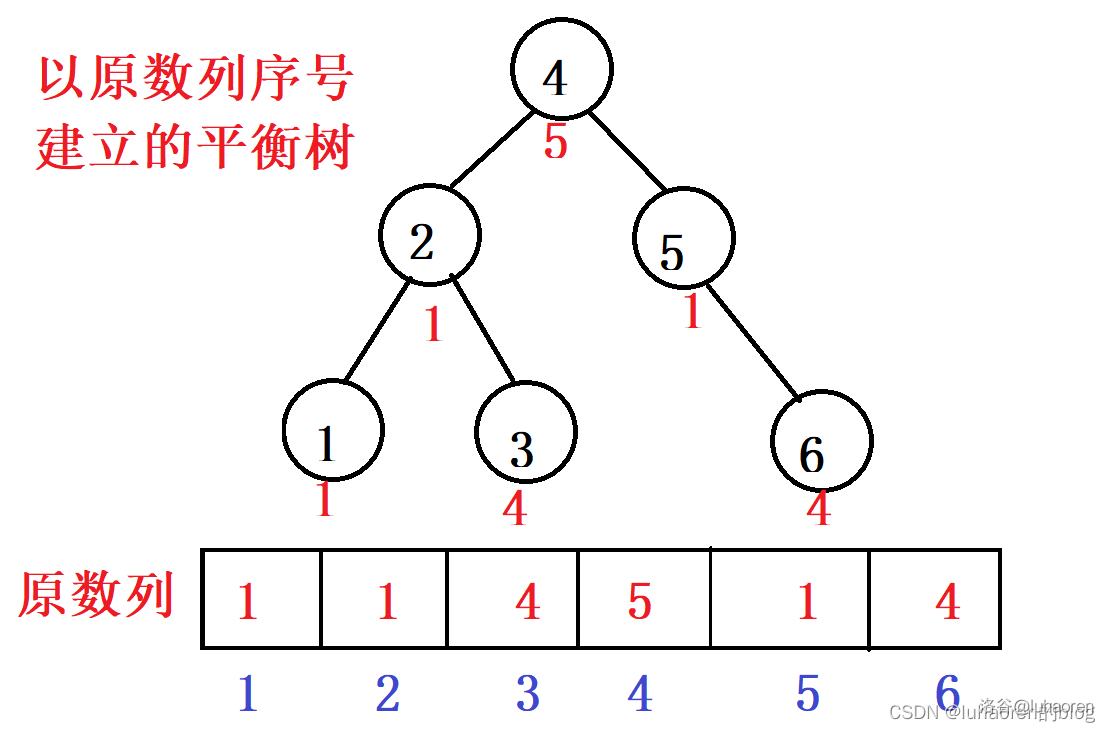
那么我们如何提取出一段区间呢？如果按值分裂，分裂后的操作很可能不符合平衡树性质（如区间翻转），所以我们用到了另一种分裂方式——按大小（排名）分裂。

假如有一个区间$[l,r]$，那么先按照$r-1$分裂成树1和树2，在把树1按$l$分裂成数3和树4，那么区间$[l,r]$就是树4所表示的区间。

于是我们就可以修改或者查询树4的信息了！

区间翻转

FHQtreap如何实现区间翻转？

假如有一个序列$\{1,1,4,5,1,4\}$，我们想翻转$[2,5]$区间。

先把[2,5]分裂出来。

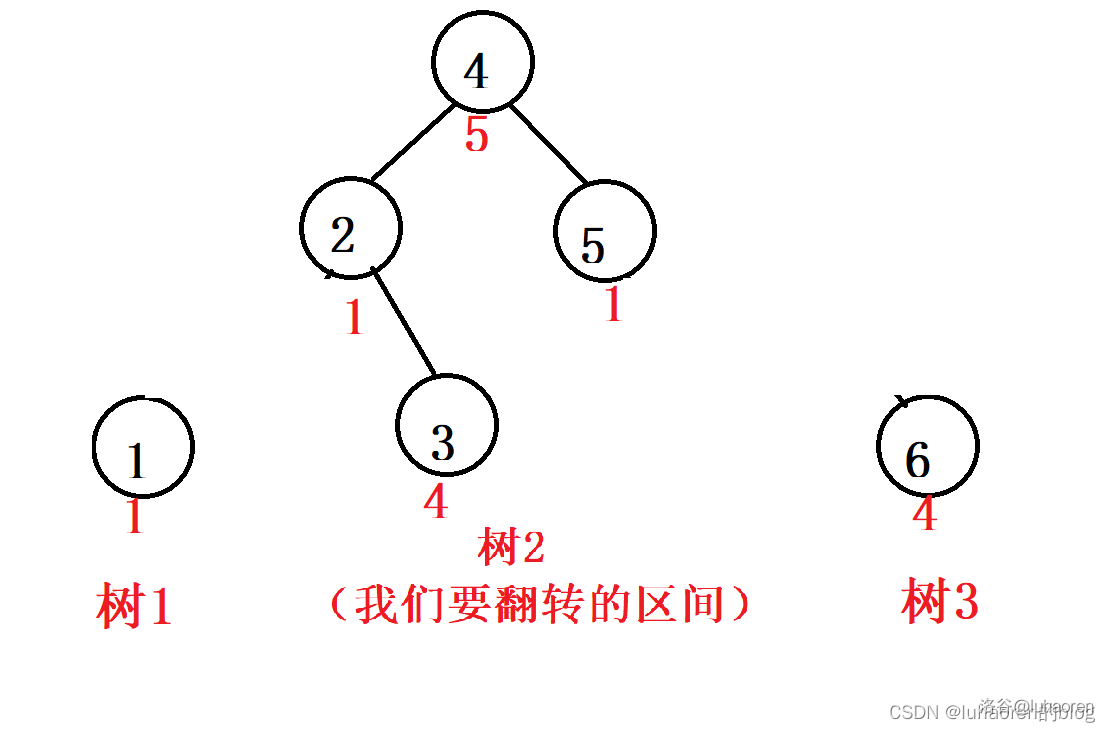
你会发现，所谓区间翻转，就是把树2自顶向下交换左右子树。

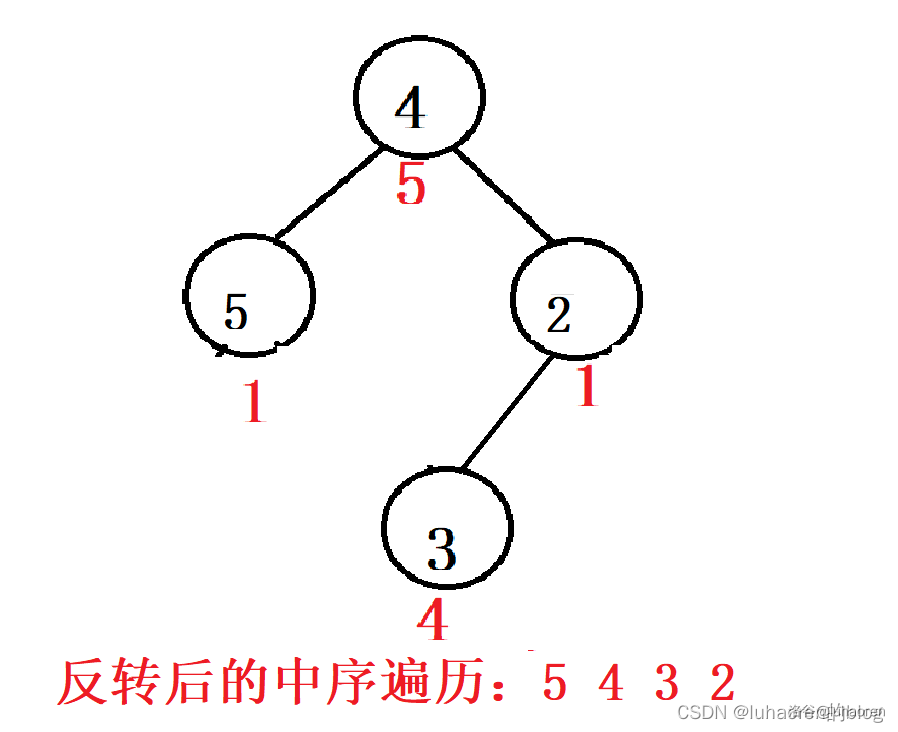
所以就可以用分裂区间$\to$自顶向下交换左右子树$\to$合并，来维护一段区间的翻转。

但是如果要依次交换这段区间内的每一个左右子树，时间复杂度就会达到$O(n)$，所以我们可以使用懒标记的方式（默认你会）维护。

给要翻转的区间树打上标记，再合并进去，这样就不影响复杂度了！

具体实现见例题·文艺平衡树。

习题

P3369 普通平衡树

原题

模板题，没什么好讲的。

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
    int x,rnd,size;
    int ls,rs;
}tr[N];
int tot=0,root=0;
void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
int newNode(int x){
    tr[++tot]={x,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,int val){
    if(!u){
        x=y=0;
        return;
    }
    if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);
    else y=u,split(tr[y].ls,x,tr[y].ls,val);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
void insert(int x){
    int l,r;
    split(root,l,r,x);
    root=merge(merge(l,newNode(x)),r);
}
void del(int x){
    int l,r,xx,yy;
    split(root,l,r,x);
    split(l,xx,yy,x-1);
    yy=merge(tr[yy].ls,tr[yy].rs);
    root=merge(merge(xx,yy),r);
}
int rnk(int x){
    int l,r;
    split(root,l,r,x-1);
    int tmp=tr[l].size+1;
    root=merge(l,r);
    return tmp;
}
int kth(int u,int k){
    int p=tr[tr[u].ls].size+1;
    if(p==k) return tr[u].x;
    if(p<k) return kth(tr[u].rs,k-p);
    return kth(tr[u].ls,k);
}
int pre(int x){
    int l,r;
    split(root,l,r,x-1);
    int tmp=kth(l,tr[l].size);
    root=merge(l,r);
    return tmp;
}
int nxt(int x){
    int l,r;
    split(root,l,r,x);
    int tmp=kth(r,1);
    root=merge(l,r);
    return tmp;
}
int n;
int main(){
    cin>>n;
    while(n--){
        int opt,x;
        cin>>opt>>x;
        if(opt==1) insert(x);
        if(opt==2) del(x);
        if(opt==3) cout<<rnk(x)<<endl;
        if(opt==4) cout<<kth(root,x)<<endl;
        if(opt==5) cout<<pre(x)<<endl;
        if(opt==6) cout<<nxt(x)<<endl;
    }
}

P1486 郁闷的出纳员

原题

设置一个$\Delta$把工资的调整记录下来。

$I$操作插入新节点时直接插入$x-\Delta$。

$S$操作时，先改$\Delta$，然后把小于$\min-\Delta$的删掉（这个用fhq做就很方便）

输出的时候别忘了加上$\Delta$。

AC代码（古早时期的代码，码风可能有点差别）

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
    int ls,rs;
    int x,rnd,size;
}tr[N];
int tot=0,root=0;
int newNode(int x){
    tr[++tot]={0,0,x,rand(),1};
    return tot;
}
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
void split(int u,int &x,int &y,int val){
    if(!u){
        x=y=0;
        return;
    }
    if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);
    else y=u,split(tr[y].ls,x,tr[y].ls,val);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
int tag=0;//tag表示工资调整
void insert(int x){
    int l,r;
    split(root,l,r,x);
    root=merge(l,merge(newNode(x),r));
}
int getNum(int u,int k){
    int p=tr[tr[u].ls].size+1;
    if(p==k) return tr[u].x;
    if(p>k) return getNum(tr[u].ls,k);
    return getNum(tr[u].rs,k-p);
}
int n,minn,ans=0;
void del(int x){
    int l,r,xx,yy;
    split(root,l,r,x);
    split(l,xx,yy,x-1);
    yy=merge(tr[yy].ls,tr[yy].rs);
    root=merge(merge(xx,yy),r);
}

int main(){
    char op;
    int x;
    cin>>n>>minn;
    for(int i=1;i<=n;i++){
        cin>>op>>x;
        if(op=='I'){
            if(x>=minn) insert(x-tag);
        }
        else if(op=='A') tag+=x;
        else if(op=='S'){
            tag-=x;
            int l=0,r=0;
            split(root,l,r,minn-tag-1);
            ans+=tr[l].size;
            root=r;
        }
        else{
            if(tr[root].size<x) cout<<-1<<endl;
            else cout<<getNum(root,tr[root].size-x+1)+tag<<endl;
        }
    }
    cout<<ans<<endl;
}

P5338 甲苯先生的滚榜

原题

题目要求排序时有两个关键词，用平衡树怎么做呢？

正常使用sort或者优先队列的时候，如果有多个关键词，我们一般会使用重载运算符，而这种多关键词的平衡树问题，我们也可以使用重载运算符，注意要重载$<$和$\le$两个运算符。

AC代码

#include <bits/stdc++.h>
using namespace std;
struct cmp{
//重载运算符的结构体
    int cnt,tim;
    bool operator<=(const cmp b)const{
        if(cnt==b.cnt) return tim<=b.tim;
        return cnt>=b.cnt;
    }
    bool operator<(const cmp b)const{
        if(cnt==b.cnt) return tim<b.tim;
        return cnt>b.cnt;
    }
};
const int N=2e6+10;
struct node{
    cmp x;
    int rnd,size;
    int ls,rs;
}tr[N];
cmp peo[N];
int tot=0,root;
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
int newNode(cmp x){
    tr[++tot]={x,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,cmp val){
    if(!u){
        x=y=0;
        return;
    }
    if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);
    else y=u,split(tr[y].ls,x,tr[y].ls,val);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
void del(cmp x){
    int l,r,xx,yy;
    split(root,l,r,x);
    split(l,xx,yy,{x.cnt,x.tim-1});//造成正常平衡树x-1的效果
    yy=merge(tr[yy].ls,tr[yy].rs);
    root=merge(merge(xx,yy),r);
}
void insert(cmp x){
    int l,r;
    split(root,l,r,x);
    root=merge(merge(l,newNode(x)),r);
}
void clear(){
//多组数据，清空直接让根指向0就行
    root=tot=0;
}
typedef unsigned int ui;
int m,n;
ui seed;
ui randNum( ui& seed , ui last , const ui m){ 
//题目要求的随机数种子（千万不要把ui什么的改了，会出错的！）
    seed = seed * 17 + last ; return seed % m + 1; 
}
int T,last=7;
int main(){
    cin>>T;
    while(T--){
        clear();
        cin>>m>>n>>seed;
        for(int i=1;i<=m;i++){
            peo[i]={0,0};
            insert(peo[i]);
        }
        for(int i=1;i<=n;i++){
            int ria=randNum(seed,last,m),rib=randNum(seed,last,m);
            del(peo[ria]);
            peo[ria].cnt++,peo[ria].tim+=rib;
            insert(peo[ria]);
            int l,r;
            split(root,l,r,{peo[ria].cnt,peo[ria].tim-1});
            last=tr[l].size;
            cout<<last<<endl;
            root=merge(l,r);            
        }
    }
    return 0;
}

P3850 书架

原题

每次插入一个数，后面每一个数的排名都会$+1$，可以把排名当成权值，每次插入就用懒标记给后面的数$+1$。

注意要保存一个书名的映射（最好直接把书名放到结构体里）

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+211;
struct node{
    int x,rnd,size;
    int ls,rs;
    int add;//懒标记
    string name;//书名
}tr[N];
int tot=0,root;
int newNode(string str,int i){
    tr[++tot]={i,rand(),1,0,0,0,str};
    return tot;
}
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
inline void pushdown(int x){
    tr[tr[x].ls].x+=tr[x].add,tr[tr[x].rs].x+=tr[x].add;
    tr[tr[x].ls].add+=tr[x].add,tr[tr[x].rs].add+=tr[x].add;
    tr[x].add=0;
}
void split(int u,int &x,int &y,int val){
    if(!u){
        x=y=0;
        return;
    }
    pushdown(u);//在分裂和并时都要下放懒标记
    if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);
    else y=u,split(tr[y].ls,x,tr[y].ls,val);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        pushdown(x);
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        pushdown(y);
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
int kth(int u,int k){
    int p=tr[tr[u].ls].size+1;
    if(p==k) return tr[u].x;
    if(p<k) return kth(tr[u].rs,k-p);
    return kth(tr[u].ls,k);
}
int n,m,q;
int main(){
    cin>>n;
    for(int i=0;i<n;i++){
        string str;
        cin>>str;
        root=merge(root,newNode(str,i));//因为插入时排名就是单调的，所以可以这样直接建树
    }
    cin>>m;
    while(m--){
        string str;
        int x,l,r;
        cin>>str>>x;
        split(root,l,r,x-1);
        tr[r].add++,tr[r].x++;//给后面的数排名加上1
        r=merge(newNode(str,x),r);
        root=merge(l,r);
    }
    cin>>q;
    while(q--){
        int x,l,r,xx,yy;
        cin>>x;
        split(root,l,r,x);
        split(l,xx,yy,x-1);
        cout<<tr[yy].name<<endl;
        root=merge(merge(xx,yy),r);
    }
    return 0;
}

P3391 文艺平衡树

原题

平衡树区间翻转的模板，我们刚刚已经讲过，直接放代码。

AC代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
struct node{
    int x,rnd,size;
    int ls,rs;
    int add;
}tr[N];
int tot=0,root=0;
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
inline void pushdown(int x){
    //pushdown和线段树的差不多
    if(tr[x].add){
        swap(tr[x].ls,tr[x].rs);
        tr[x].add=0;
        if(tr[x].ls) tr[tr[x].ls].add^=1;
        if(tr[x].rs) tr[tr[x].rs].add^=1;
    }
}
int newNode(int x){
    tr[++tot]={x,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,int size){
    if(!u){
        x=y=0;
        return;
    }
    pushdown(u);//每次分裂合并前都要下放标记
    if(tr[tr[u].ls].size<size) x=u,split(tr[u].rs,tr[u].rs,y,size-tr[tr[u].ls].size-1);
    else y=u,split(tr[u].ls,x,tr[u].ls,size);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        pushdown(x);
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        pushdown(y);
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
void put(int x){
    if(!x) return;
    pushdown(x);//输出时也要先下放标记
    put(tr[x].ls);
    cout<<tr[x].x<<" ";
    put(tr[x].rs);
}
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        root=merge(root,newNode(i));
    for(int i=1;i<=m;i++){
        int l,r;
        cin>>l>>r;
        int x,y,xx,yy;
        split(root,x,y,l-1);
        split(y,xx,yy,r-l+1);
        tr[xx].add^=1;
        y=merge(xx,yy);
        root=merge(x,y);
    }
    put(root);
}

P4146 序列终结者

原题

平衡树维护区间信息的模板题。

大意是要维护区间最大值，另外要维护区间加和区间翻转。

维护两个懒标记即可，每个节点维护一个最大值，表示当前子树内最大的数。

AC代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct node{
    int val,maxx,tag,add;
    int rnd,size;
    int ls,rs;
}tr[N];
int tot=0,root;
void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
    tr[x].maxx=max({tr[x].val,tr[tr[x].ls].maxx,tr[tr[x].rs].maxx});
    //这里的pushup操作除了维护子树大小，还要维护一个区间最大值
}
void pushdown(int x){
    if(tr[x].add){
        //区间加懒标记，和线段树差不多，但是要加上节点本身
        tr[tr[x].ls].maxx+=tr[x].add,tr[tr[x].rs].maxx+=tr[x].add;
        tr[tr[x].ls].val+=tr[x].add,tr[tr[x].rs].val+=tr[x].add;
        tr[tr[x].ls].add+=tr[x].add,tr[tr[x].rs].add+=tr[x].add;
        tr[x].add=0;
    }
    if(tr[x].tag){
        //区间翻转
        swap(tr[x].ls,tr[x].rs);
        tr[tr[x].ls].tag^=1,tr[tr[x].rs].tag^=1;
        tr[x].tag=0;
    }
}
int newNode(int x){
    tr[++tot]={x,x,0,0,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,int size){
    if(!u){
        x=y=0;
        return;
    }
    pushdown(u);//每次分裂合并前都要下传标记
    if(tr[tr[u].ls].size<size) x=u,split(tr[u].rs,tr[u].rs,y,size-tr[tr[u].ls].size-1);
    else y=u,split(tr[u].ls,x,tr[u].ls,size);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        pushdown(x);
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        pushdown(y);
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
int n,m;
signed main(){
    cin>>n>>m;
    tr[0].maxx=-1e18;
    for(int i=1;i<=n;i++) root=merge(root,newNode(0));
    for(int i=1;i<=m;i++){
        int opt,l,r,v;
        int x,y,z,k;
        cin>>opt>>l>>r;
        if(opt==1){
            //区间加
            cin>>v;
            split(root,x,y,r);
            split(x,z,k,l-1);
            //和线段树懒标记差不多
            tr[k].add+=v,tr[k].maxx+=v,tr[k].val+=v;
            x=merge(z,k);
            root=merge(x,y);
        }
        if(opt==2){
            //区间翻转
            split(root,x,y,r);
            split(x,z,k,l-1);
            tr[k].tag^=1;
            x=merge(z,k);
            root=merge(x,y);
        }
        if(opt==3){
            //直接输出区间最大值
            split(root,x,y,r);
            split(x,z,k,l-1);
            cout<<tr[k].maxx<<endl;
            x=merge(z,k);
            root=merge(x,y);
        }
    }
    return 0;
}

P4008 文本编辑器

原题

删除区间，插入区间，输出区间。

这题的输入比较坑，需要注意。

AC代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e6+10;
struct node{
    char ch;
    int rnd,size;
    int ls,rs;
}tr[N];
int tot=0,root;
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
}
int newNode(char ch){
    tr[++tot]={ch,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,int size){
    if(!u){
        x=y=0;
        return;
    }
    if(tr[tr[u].ls].size<size) x=u,split(tr[u].rs,tr[u].rs,y,size-tr[tr[u].ls].size-1);
    else y=u,split(tr[u].ls,x,tr[y].ls,size);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
void put(int x){
    if(!x) return;
    put(tr[x].ls);
    putchar(tr[x].ch);
    put(tr[x].rs);
}
int build(int n,string s){
    int u=newNode(s[0]);
    for(int i=1;i<n;i++) u=merge(u,newNode(s[i]));
    return u;
}
int gb=0,T;
int main(){
    cin>>T;
    for(int i=1;i<=T;i++){
        string opt;
        int l,r,xx,yy,n;
        cin>>opt;
        if(opt=="Move") cin>>gb;
        if(opt=="Insert"){
            cin>>n;
            string tmp={};
            for(int i=0;i<n;i++){
                char ch=getchar();
                while(ch<32||ch>126) ch=getchar();
                tmp+=ch;
            }
            int u=build(n,tmp);
            split(root,l,r,gb);
            root=merge(merge(l,u),r);
        }
        if(opt=="Delete"){
            cin>>n;
            split(root,l,r,n+gb);
            split(l,xx,yy,gb);
            root=merge(xx,r);
        }
        if(opt=="Get"){
            cin>>n;
            split(root,l,r,n+gb);
            split(l,xx,yy,gb);
            put(yy);//中序遍历输出
            putchar('\n');
            root=merge(merge(xx,yy),r);
        }
        if(opt=="Prev") gb--;
        if(opt=="Next") gb++;
    }
}

P3372 【模板】线段树 1

原题

达成成就，用线段树写平衡树，用平衡树写线段树……

AC代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+10;
struct node{
    int val,sum,add;
    int rnd,size;
    int ls,rs;
}tr[N];
inline void pushup(int x){
    tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
    tr[x].sum=tr[tr[x].ls].sum+tr[tr[x].rs].sum+tr[x].val;
}
inline void pushdown(int x){
    tr[tr[x].ls].sum+=tr[tr[x].ls].size*tr[x].add;
    tr[tr[x].rs].sum+=tr[tr[x].rs].size*tr[x].add;
    tr[tr[x].ls].add+=tr[x].add,tr[tr[x].rs].add+=tr[x].add;
    tr[tr[x].ls].val+=tr[x].add,tr[tr[x].rs].val+=tr[x].add;
    tr[x].add=0;
}
int tot=0,root;
int newNode(int x){
    tr[++tot]={x,x,0,rand(),1,0,0};
    return tot;
}
void split(int u,int &x,int &y,int size){
    if(!u){
        x=y=0;
        return;
    }
    pushdown(u);
    if(tr[tr[u].ls].size<size) x=u,split(tr[u].rs,tr[u].rs,y,size-tr[tr[u].ls].size-1);
    else y=u,split(tr[u].ls,x,tr[u].ls,size);
    pushup(u);
}
int merge(int x,int y){
    if(!x||!y) return x+y;
    if(tr[x].rnd<tr[y].rnd){
        pushdown(x);
        tr[x].rs=merge(tr[x].rs,y);
        pushup(x);
        return x;
    }
    else{
        pushdown(y);
        tr[y].ls=merge(x,tr[y].ls);
        pushup(y);
        return y;
    }
}
int n,m;
signed main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        int x;
        cin>>x;
        root=merge(root,newNode(x));
    }
    while(m--){
        int opt,x,y,k,l,r,xx,yy;
        cin>>opt>>x>>y;
        if(opt==1){
            cin>>k;
            split(root,l,r,y);
            split(l,xx,yy,x-1);
            tr[yy].add+=k;
            tr[yy].sum+=tr[yy].size*k;
            tr[yy].val+=k;
            root=merge(merge(xx,yy),r);
        }
        else{
            split(root,l,r,y);
            split(l,xx,yy,x-1);
            cout<<tr[yy].sum<<endl;
            root=merge(merge(xx,yy),r);
        }
    }
    return 0;
}

P3380 二逼平衡树（树套树）

原题

这种动态的区间排名问题一般用树套树（线段树套平衡树）解决。

树套树，就是先建一颗平衡树，在每个节点内建一颗平衡树，插入这个区间内的所有树，均摊空间复杂度大概是$O(\log n)$

查询$k$在区间内的排名，可以在所有包含区间内找小于$k$的数的个数，都加起来在$+1$。时间复杂度$O(\log^2 n)$。

修改某一位值上的数值，找所有包含这这个数的节点，在这些节点上删去这个数，在插入新的数。时间复杂度也是$O(\log^2 n)$。

查询$k$在区间内的前驱，在所有包含区间内找$k$的前驱，取最大值；同理，后继就是取最小值了。时间复杂度是$O(\log^2 n)$。

唯一复杂的是查询区间内排名为$k$的值，我们可以用二分答案的方法，在$[0,10^8]$的范围内二分，判断这个数排名是不是$k$，时间复杂度是$O(\log^3 n)$。

树套树写起来比较复杂，可以锻炼码力和调试能力（我当时调了两周）

AC代码

#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e4+10,inf=2147483647;
namespace FHQ{
    //把平衡树封装
    struct node{
        int x,rnd,size;
        int ls,rs;
    }tr[N<<6];
    int tot=0;
    class fhq{
    public:
        int root;
        int newNode(int x){
            tr[++tot]={x,rand(),1,0,0};
            return tot;
        }
        inline void pushup(int x){
            tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;
        }
        void split(int u,int &x,int &y,int val){
            if(!u){
                x=y=0;
                return;
            }
            if(tr[u].x<=val) x=u,split(tr[x].rs,tr[x].rs,y,val);
            else y=u,split(tr[y].ls,x,tr[y].ls,val);
            pushup(u);
        }
        int merge(int x,int y){
            if(!x||!y) return x+y;
            if(tr[x].rnd<tr[y].rnd){
                tr[x].rs=merge(tr[x].rs,y);
                pushup(x);
                return x;
            }
            else{
                tr[y].ls=merge(x,tr[y].ls);
                pushup(y);
                return y;
            }
        }
        void insert(int x){
            int l,r;
            split(root,l,r,x);
            root=merge(l,merge(newNode(x),r));
        }
        void del(int x){
            int l,r,xx,yy;
            split(root,l,r,x);
            split(l,xx,yy,x-1);
            yy=merge(tr[yy].ls,tr[yy].rs);
            root=merge(merge(xx,yy),r);
        }
        int rnk(int x){
            int l,r;
            split(root,l,r,x-1);
            int tmp=tr[l].size+1;
            root=merge(l,r);
            return tmp;
        }
        int kth(int u,int k){
            int p=tr[tr[u].ls].size+1;
            if(k==p) return tr[u].x;
            if(k<p) return kth(tr[u].ls,k);
            return kth(tr[u].rs,k-p);
        }
        inline int getKth(int x){
            return kth(root,x);
        }
        int pre(int x){
            int l,r;
            split(root,l,r,x-1);
            int tmp=kth(l,tr[l].size);
            root=merge(l,r);
            return tmp;
        }
        int nxt(int x){
            int l,r;
            split(root,l,r,x);
            int tmp=kth(r,1);
            root=merge(l,r);
            return tmp;
        }
    };
}
struct node{
    int l,r;
    int maxx,minn;
}tr[N<<2];
FHQ::fhq tree[N<<2];
int a[N];
int n,m;
inline void pushup(int x){
    tr[x].maxx=max(tr[x*2].maxx,tr[x*2+1].maxx);
    tr[x].minn=min(tr[x*2].minn,tr[x*2+1].minn);
}
void build(int x,int l,int r){
    tr[x].l=l,tr[x].r=r;
    for(int i=l;i<=r;i++) tree[x].insert(a[i]);
    if(l==r){
        tr[x].maxx=tr[x].minn=a[l];
        return;
    }
    int mid=(l+r)/2;
    build(x*2,l,mid),build(x*2+1,mid+1,r);
    pushup(x);
}
int rnk(int x,int l,int r,int k){
    if(tr[x].l>=l&&tr[x].r<=r) return tree[x].rnk(k);
    int mid=(tr[x].l+tr[x].r)/2,res=1;
    if(l<=mid) res+=rnk(x*2,l,r,k)-1;
    if(r>mid) res+=rnk(x*2+1,l,r,k)-1;
    return res;
}
int kth(int l,int r,int k){
    int x=0,y=1e8+10,ans=0;
    while(x<=y){
        int mid=(x+y)/2,tmp=rnk(1,l,r,mid);
        if(tmp<=k) x=mid+1,ans=mid;
        else y=mid-1;
    }
    return ans;
}
int pre(int x,int l,int r,int k){
    if(tr[x].l>=l&&tr[x].r<=r){
        if(tr[x].minn>=k) return -inf;
        return tree[x].pre(k);
    }
    int mid=(tr[x].l+tr[x].r)/2,maxx=-inf;
    if(l<=mid) maxx=max(maxx,pre(x*2,l,r,k));
    if(r>mid) maxx=max(maxx,pre(x*2+1,l,r,k));
    return maxx;
}
int nxt(int x,int l,int r,int k){
    if(tr[x].l>=l&&tr[x].r<=r){
        if(tr[x].maxx<=k) return inf;
        return tree[x].nxt(k);
    }
    int mid=(tr[x].l+tr[x].r)/2,minn=inf;
    if(l<=mid) minn=min(minn,nxt(x*2,l,r,k));
    if(r>mid) minn=min(minn,nxt(x*2+1,l,r,k));
    return minn;
}
void change(int x,int k,int p){
    tree[x].del(a[k]);
    tree[x].insert(p);
    if(tr[x].l==tr[x].r){
        tr[x].maxx=tr[x].minn=a[k]=p;
        return;
    }
    int mid=(tr[x].l+tr[x].r)/2;
    if(k<=mid) change(x*2,k,p);
    else change(x*2+1,k,p);
    pushup(x);
}
signed main(){
    srand(19260817);
    scanf("%lld%lld",&n,&m);
    for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
    build(1,1,n);
    while(m--){
        int opt,l,r,k;
        scanf("%lld%lld%lld",&opt,&l,&r);
        if(opt!=3) scanf("%lld",&k);
        if(opt==1) printf("%lld\n",rnk(1,l,r,k));
        if(opt==2) printf("%lld\n",kth(l,r,k));
        if(opt==3) change(1,l,r);
        if(opt==4) printf("%lld\n",pre(1,l,r,k));
        if(opt==5) printf("%lld\n",nxt(1,l,r,k));
    }
}