NOIP2015普及组初赛错题总结

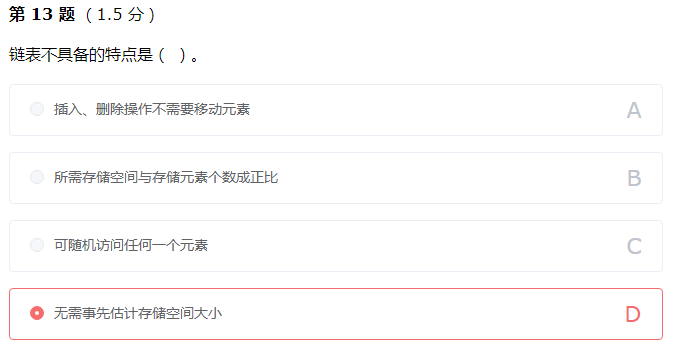
13.

for(int i=h[a];~i;i=ne[i])
{
BLABALBALBALBABLBAL;
}
这样才能找到一个数所以这个的时间复杂度是O(n)

21重新排列 1234 使得每一个数字都不在原来的位置上，一共有（ ）种排法。

错排问题。 问题规模较小，也可以手动枚举。错排的方案有：
2143、2341、2413、3142、3412、3421、4123、4312、4321，一共9种。
解决错排问题的算法思想是将排列第n个数的情况f(n)f(n)分为两类：

前面n−1n−1个数已经完成错排，那么从前面n−1n−1个数中任意挑出一个数与第nn个数进行交换，此时构成nn个数的错排，方案总数为(n−1)×f(n−1)(n−1)×f(n−1)。
前面n−1n−1个数只有一个数在自己原来位置，即已经构成n−2n−2个数的错排，此时将该数与第nn个数进行交换，则也能构成nn个数的错排，方案总数为(n−1)×f(n−2)(n−1)×f(n−2)。
所以，nn个数的错排方案总数为：f(n)=(n−1)×(f(n−1)+f(n−2))f(n)=(n−1)×(f(n−1)+f(n−2))。
初始状态：f(1)=0,f(2)=1,f(3)=2,f(4)=9f(1)=0,f(2)=1,f(3)=2,f(4)=9