历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

强连通分量

作者：

啦啦啦_199 , 2023-07-25 22:10:21 , 所有人可见 , 阅读 244

2

1

P2863 [USACO06JAN] The Cow Prom S
模板题

[USACO06JAN] The Cow Prom S

题目描述

有一个 $n$ 个点， $m$ 条边的有向图，请求出这个图点数大于 $1$ 的强连通分量个数。

输入格式

第一行为两个整数 $n$ 和 $m$ 。

第二行至 $m+1$ 行，每一行有两个整数 $a$ 和 $b$ ，表示有一条从 $a$ 到 $b$ 的有向边。

输出格式

仅一行，表示点数大于 $1$ 的强连通分量个数。

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

对于全部的测试点，保证 $2\le n \le 10^4$ ， $2\le m\le 5\times 10^4$ ， $1 \leq a, b \leq n$ 。

import java.io.*;
import java.util.*;

public class Main{
    static int N = 10010,M = 50010;
    static int[] h = new int[N],e = new int[M],ne = new int[M];
    static int[] dfn = new int[N],low = new int[N],
    stk = new int[N],size = new int[N];
    static boolean[] in_stk = new boolean[N];
    static int n,m,idx = 0,stkTop = 0,scc_cnt = 0,timestamp = 0;
    static BufferedReader br
        = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer sc = new StreamTokenizer(br);
    public static void main(String[] args)throws IOException{
        n = nextRead();
        m = nextRead();
        Arrays.fill(h,-1);
        for(int i = 1;i<=m;i++){
            int a = nextRead();
            int b = nextRead();
            add(a,b);
        }

        for(int i = 1;i<=n;i++)
            if(dfn[i] == 0)
                tarjan(i);

        int cnt = 0;
        for(int i = 1;i<=scc_cnt;i++)
            if(size[i]>1) cnt++;

        System.out.println(cnt);
    }
    public static void tarjan(int u){
        dfn[u] = low[u] = ++timestamp;
        in_stk[u] = true;
        stk[stkTop++] = u;
        for(int i = h[u];i!=-1;i = ne[i]){
            int j = e[i];
            if(dfn[j] == 0){
                tarjan(j);
                low[u] = Math.min(low[j],low[u]);
            }else if(in_stk[j])
                low[u] = Math.min(low[u],dfn[j]);
        }
        if(dfn[u] == low[u]){
            int y = -1;
            scc_cnt++;
            do{
                y = stk[--stkTop];
                size[scc_cnt]++;
                in_stk[y] = false;
            }while(y!=u);
        }
    }
    public static void add(int a,int b){
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    public static int nextRead()throws IOException{
        sc.nextToken();
        return (int)sc.nval;
    }
}

性质1：给定一个缩点后的DAG,设入度为0的点为cnt1,出度为0的点为cnt2,
变成scc需要加的最少边数:min(cnt1,cnt2)
P7251 [JSOI2014] 强连通图

[JSOI2014] 强连通图

题目描述

JYY 最近痴迷于图的强连通性，所以对于任何有向图，JYY 都希望增加一些边使得这个图变成强连通图。JYY现在得到了一个 $n$ 个点 $m$ 条边的有向图，所有点从 $1$ 到 $n$ 编号。

JYY 想知道：

在给定的图中，最多能选出多少个点，使得这些点在原图中两两可达？
在给定的图中，最少增加多少条边，可以使得这个图变成强连通图？

其中，一个有向图 $G(V,E)$ 是强连通的，当且仅当任意顶点 $a,b\in V,a\neq b$ 之间都存在 $a\to b$ 和 $b\to a$ 的路径。

输入格式

第一行包含两个整数 $n$ 和 $m$ 。

接下来 $m$ 行，每行两个整数 $x$ 和 $y$ ，表示图中有一条从 $x$ 到 $y$ 的有向边。

输出格式

两行，第一行表示第一个问题的答案，第二行表示第二个问题的答案。

样例 #1

样例输入 #1

样例输出 #1

1
2

提示

样例解释 1

对于第一个问题，无法选出互相连通两个点，答案为 $1$ 。

对于第二个问题，一种加边数最小的方案为 $(3,1)$ 和 $(4,2)$ ，答案为 $2$ 。

数据范围

对于 $100\%$ 的数据， $1\leq n\leq 10^5,1\leq m\leq 3\times 10^5$ 。

#include <bits/stdc++.h>

const int N = 100010,M = 500010;

typedef long long LL;

using namespace std;

int h[N],hs[N],e[M],ne[M],cnt[N],f[N];
int dfn[N],low[N],id[N],stk[N],din[N],dout[N];
bool in_stk[N];
int n,m,stkTop,idx,timestamp,scc_cnt;
void add(int h[],int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void tarjan(int u){
    dfn[u] = low[u] = ++timestamp;
    stk[stkTop++] = u;
    in_stk[u] = true;
    for(int i = h[u];i!=-1;i = ne[i]){
        int j = e[i];
        if(dfn[j] == 0){
            tarjan(j);
            low[u] = min(low[u],low[j]);
        }else if(in_stk[j])
            low[u] = min(low[u],dfn[j]);
    }
    if(dfn[u] == low[u]){
        int y = -1;
        ++scc_cnt;
        do{
            y = stk[--stkTop];
            in_stk[y] = false;
            id[y] = scc_cnt;
            cnt[scc_cnt]++;
        }while(y!=u);
    }
}
int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    for(int i = 1;i<=m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(h,a,b);
    }
    for(int i = 1;i<=n;i++)
        if(dfn[i] == 0)
            tarjan(i);

    for(int i = 1;i<=n;i++){
        for(int j = h[i];j!=-1;j = ne[j]){
            int k = e[j];
            int a = id[i],b = id[k];
            if(a!=b){
                din[b]++;
                dout[a]++;
            }
        }
    }
    int inzero = 0,outzero = 0,res = 0;
    for(int i = 1;i<=scc_cnt;i++){
        if(din[i] == 0) inzero++;
        if(dout[i] == 0) outzero++;
        res = max(res,cnt[i]);
    }
    outzero = max(inzero,outzero);
    if(scc_cnt == 1) outzero = 0;
    printf("%d\n",res);
    printf("%d\n",outzero);
    return 0;
}

性质2:scc_cnt的逆序就是拓扑序

[JSOI2010] 连通数

题目背景

本题数据过水，可前往 https://www.luogu.com.cn/problem/U143178 提交

$\text{upd 2022.8.4}$ ：已作为 Hack 数据合并进来。

题目描述

度量一个有向图连通情况的一个指标是连通数，指图中可达顶点对个的个数。

如图

qwq

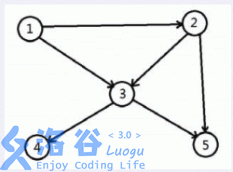
顶点 $1$ 可达 $1, 2, 3, 4, 5$

顶点 $2$ 可达 $2, 3, 4, 5$

顶点 $3$ 可达 $3, 4, 5$

顶点 $4, 5$ 都只能到达自身。

所以这张图的连通数为 $14$ 。

给定一张图，请你求出它的连通数

输入格式

输入数据第一行是图顶点的数量，一个正整数 $N$ 。
接下来 $N$ 行，每行 $N$ 个字符。第 $i$ 行第 $j$ 列的 1 表示顶点 $i$ 到 $j$ 有边，0 则表示无边。

输出格式

输出一行一个整数，表示该图的连通数。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $100 \%$ 的数据， $1 \le N \le 2000$ 。

#include <bits/stdc++.h>

const int N = 2050,M = 4000500;

typedef long long LL;

using namespace std;

int h[N],hs[N],e[M],ne[M],d[N];
int dfn[N],low[N],id[N],stk[N];
LL cnt[N];
bool in_stk[N];
int n,m,stkTop,idx,timestamp,scc_cnt,INF = 0x3f3f3f3f;
void add(int h[],int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

void tarjan(int u){
    dfn[u] = low[u] = ++timestamp;
    stk[stkTop++] = u;
    in_stk[u] = true;
    for(int i = h[u];i!=-1;i = ne[i]){
        int j = e[i];
        if(dfn[j] == 0){
            tarjan(j);
            low[u] = min(low[j],low[u]);
        }else if(in_stk[j])
            low[u] = min(low[u],dfn[j]);
    }
    if(dfn[u] == low[u]){
        int y = -1;
        ++scc_cnt;
        do{
            y = stk[--stkTop];
            id[y] = scc_cnt;
            in_stk[y] = false;
            cnt[scc_cnt]++;
        }while(u!=y);
    }
}

int main(){
    scanf("%d",&n);
    memset(h,-1,sizeof h);
    memset(hs,-1,sizeof hs);
    for(int i = 1;i<=n;i++){
        char str[n+2];
        scanf("%s",str);
        for(int j = 1;j<=n;j++)
            if(str[j-1] == '1')
                add(h,i,j);
    }

    for(int i = 1;i<=n;i++)
        if(dfn[i] == 0)
            tarjan(i);

    unordered_set<int> set;
    for(int i = 1;i<=n;i++)
        for(int j = h[i];j!=-1;j = ne[j]){
            int k = e[j];
            int a = id[i],b = id[k];
            LL hash = (LL)a*N+b;
            if(set.find(hash)!=set.end()) continue;
            if(a!=b){
                add(hs,a,b);
                set.insert(hash);
            }
        }
    LL res = 0;
    bitset<N> hh[N];
    for(int i = 1;i<=scc_cnt;i++){
        hh[i][i] = 1;
        for(int j = hs[i];j!=-1;j = ne[j]){
            int k = e[j];
            hh[i]|=hh[k];
        }
    }
    for(int i = 1;i<=scc_cnt;i++)
        for(int j = 1;j<=scc_cnt;j++)
            if(hh[i][j]) res+=cnt[i]*cnt[j];
    printf("%lld",res);
    return 0;
}

杀人游戏

[中山市选] 杀人游戏

题目描述

一位冷血的杀手潜入Na-wiat，并假装成平民。警察希望能在 $N$ 个人里面，查出谁是杀手。警察能够对每一个人进行查证，假如查证的对象是平民，他会告诉警察，他认识的人，谁是杀手，谁是平民。假如查证的对象是杀手，杀手将会把警察干掉。现在警察掌握了每一个人认识谁。每一个人都有可能是杀手，可看作他们是杀手的概率是相同的。

问：根据最优的情况，保证警察自身安全并知道谁是杀手的概率最大是多少？

输入格式

第一行有两个整数 $N,M$ 。
接下来有 $M$ 行，每行两个整数 $x,y$ ，表示 $x$ 认识 $y$ （ $y$ 不一定认识 $x$ ,例如President同志）。

注：原文zz敏感内容已替换

输出格式

仅包含一行一个实数，保留小数点后面 $6$ 位，表示最大概率。

样例 #1

样例输入 #1

样例输出 #1

0.800000

提示

警察只需要查证 $1$ 。假如 $1$ 是杀手，警察就会被杀。假如 $1$ 不是杀手，他会告诉警察 $2,3,4,5$ 谁是杀手。而 $1$ 是杀手的概率是 $0.2$ ，所以能知道谁是杀手但没被杀的概率是 $0.8$ 。

对于 $100\%$ 的数据有 $1≤N≤100000,0≤M≤300000$ 。

分析:
按照关系建图，在建立完毕之后，这个图会存在许许多多的环，环内的元素一定都能互相到达，即强连通分量
对于强连通分量，我们只需要知道里面某个点的身份，就能知道整个分量的身份
我们可以用tarjan求一下所有的强连通分量，然后缩点，将原图变成DAG，那么只需要对所有入度为0的分量询问
就可以知道所有分量的身份，假设入度为0的分量个数为x(注意：可以查任意多个人(一开始我以为只能看一个人emmm))
只需要在每个入度为0的分量挑一个就行了(因为根据拓扑序，后面的人都能到达)，那么我们就选了x个人,那么这x个人
不是凶手的概率为1-x/n
注意！！
还有一种特殊情况
特殊分析.png
若A连通分量的大小只有1，那么根据排除法,只要知道了其他人的身份,A的身份肯定也能知道，即其他人都是好人，A肯定是坏人，其他人中有坏人，A肯定是好人，所以要特判一下这种情况，此时概率变为1-(x-1)/n

代码:

import java.io.*;
import java.util.*;

public class Main{
    static int N = 100010,M = 200010;
    static int[] h = new int[N],hs = new int[N],
    e = new int[M],ne = new int[M],id = new int[N];
    static int[] dfn = new int[N],low = new int[N],
    stk = new int[N],size = new int[N],d = new int[N];
    static boolean[] in_stk = new boolean[N];
    static int n,m,idx = 0,timestamp = 0,stkTop = 0,scc_cnt = 0;
    static BufferedReader br 
        = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer sc = new StreamTokenizer(br);
    public static void main(String[] args)throws IOException{
        n = nextRead();
        m = nextRead();
        Arrays.fill(h,-1);
        Arrays.fill(hs,-1);
        for(int i = 1;i<=m;i++){
            int a = nextRead();
            int b = nextRead();
            add(h,a,b);
        }

        for(int i = 1;i<=n;i++)
            if(dfn[i] == 0)
                tarjan(i);

        HashSet<Long> set = new HashSet<>();
        for(int i = 1;i<=n;i++)
            for(int j = h[i];j!=-1;j = ne[j]){
                int k = e[j];
                int a = id[i],b = id[k];
                long hash = (long)a*N+b;
                if(a == b) continue;
                if(set.contains(hash)) continue;
                set.add(hash);
                add(hs,a,b);
                d[b]++;
            }

        double ans = 0D;
        int sum = 0;
        for(int i = 1;i<=scc_cnt;i++)
            if(d[i] == 0) sum++;
        for(int i = 1;i<=scc_cnt;i++){
            boolean flag = false;
            if(size[i]!=1||d[i]!=0) continue;
            for(int j = hs[i];j!=-1;j = ne[j]){
                int k = e[j];
                if(d[k] == 1) flag = true;
            }
            if(!flag){
                sum--;
                break;
            }
        }
        ans = 1.0-1.0*sum/n;
        System.out.printf("%.6f",ans);
    }
    public static void tarjan(int u){
        dfn[u] = low[u] = ++timestamp;
        stk[stkTop++] = u;
        in_stk[u] = true;
        for(int i = h[u];i!=-1;i = ne[i]){
            int j = e[i];
            if(dfn[j] == 0){
                tarjan(j);
                low[u] = Math.min(low[u],low[j]);
            }else if(in_stk[j])
                low[u] = Math.min(low[u],dfn[j]);
        }
        if(dfn[u] == low[u]){
            int y = -1;
            ++scc_cnt;
            do{
                y = stk[--stkTop];
                in_stk[y] = false;
                id[y] = scc_cnt;
                size[scc_cnt]++;
            }while(y!=u);
        }
    }
    public static void add(int[] h,int a,int b){
        e[idx] = b;
        ne[idx] = h[a];
        h[a] = idx++;
    }
    public static int nextRead()throws IOException{
        sc.nextToken();
        return (int)sc.nval;
    }
}

0 评论

App 内打开