向量叉乘公式:

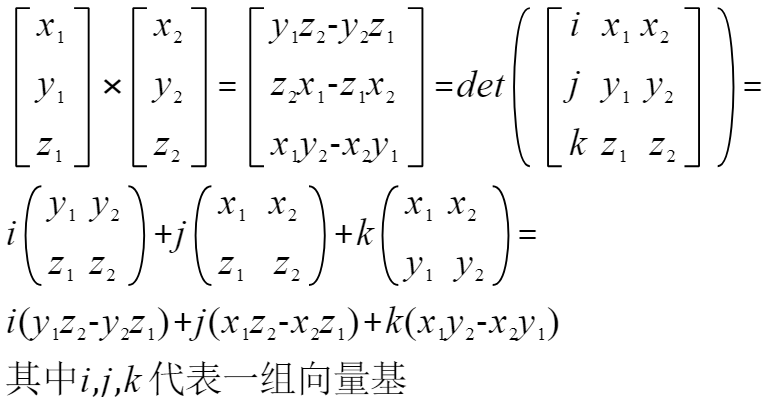
行列式为一个数,而w为一个向量，构造一个向量到数的映射，用点乘即可

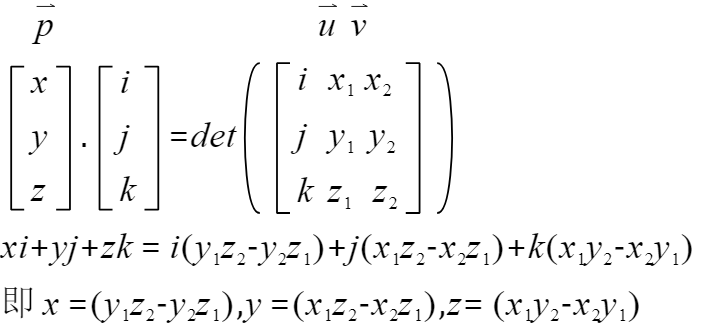
代码如下:

#include<iostream>
#include<cmath>
#include<assert.h>

using namespace std;

const double VPI = 3.14159265358979323846332854;
const double EPS = 1e-6;

struct Vec3{
    int x,y,z;

    bool operator == (const Vec3& a) const{
        return x == a.x && y == a.y && z == a.z;
    }

    bool operator != (const Vec3& a) const{
        return x != a.x || y != a.y || z != a.z;
    }

    friend Vec3 operator * (Vec3& a,int num){
        a.x *= num;
        a.y *= num;
        a.z *= num;
        return a;
    }

    friend Vec3 operator *= (Vec3& a,int num){
        a.x *= num;
        a.y *= num;
        a.z *= num;
        return a;
    }

    friend Vec3 operator + (const Vec3& a,const Vec3& b){
        return {a.x + b.x,a.y + b.y,a.z + b.z};
    }

    friend int operator * (const Vec3& a,const Vec3& b){
        return a.x * b.x + a.y * b.y + a.z * b.z;
    }

    int dot(const Vec3& b){
        return x * b.x + y * b.y + z * b.z;
    }

    Vec3 cross(Vec3& other){
        //计算三阶行列式的二阶余子式
        auto i = y * other.z - z * other.y; 
        auto j = z * other.x - x * other.z;
        auto k = x * other.y - y * other.x;
        //i,j,k 为基坐标
        return {i,j,k};
    }

    Vec3 cross2(Vec3& other){
        //计算三阶行列式的二阶余子式
        auto i = y * other.z - z * other.y; 
        auto j = z * other.x - x * other.z;
        auto k = x * other.y - y * other.x;
        //基向量
        Vec3 baseX = {1,0,0};
        Vec3 baseY = {0,1,0};
        Vec3 baseZ = {0,0,1};

        return baseX * i + baseY * j + baseZ * k;
    }

    double length() const{
        auto d = x * x + y * y + z * z;
        return sqrt(d);
    }

    double angleTo(const Vec3& other){
        auto d = dot(other);
        auto len1 = length();
        auto len2 = other.length();
        auto t = d / (len1 * len2);
        return acos(t);
    }
};

bool equalD(double a,double b){
    return abs(a - b) < EPS;
}

ostream& operator << (ostream& os, const Vec3& v)
{
   string s = "";
   s += '(';
   s += to_string(v.x);
   s += ',';
   s += to_string(v.y);
   s += ',';
   s += to_string(v.z);
   s += ')';
   os << s;
   return os;
}

int main(){
    Vec3 a = {1,2,3};
    Vec3 b = {1,2,3};
    assert(a == b);
    a *= 3;
    cout << a << endl;
    Vec3 c = {5,3,0};
    Vec3 d = {2,7,0};
    // 叉乘 cross 和 cross2是等价的
    auto e = c.cross(d);
    auto f = c.cross2(d);
    cout << e << endl;
    assert(e == f);

    auto acd = c.angleTo(d);
    auto lc = c.length();
    auto ld = d.length();

    //向量 c,d 张成的平行四边形的面积
    auto scd = lc * ld * sin(acd);
    //向量 c,d 叉积的模长
    auto elen = e.length();

    assert(equalD(scd,elen));
    //叉积e,与向量 c,d都垂直
    assert(e * c == 0);
    assert(e * d == 0);
    //叉积 e 的z 应该是大于 0

    assert(e.z > 0);

    auto h = d.cross2(c);
    cout << h << endl;

    assert(h.z < 0);

    return 0;
}