“访问”美术馆

题目描述

经过数月的精心准备，Peer Brelstet，一个出了名的盗画者，准备开始他的下一个行动。艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。Peer知道每个展室里藏画的数量，并且他精确测量了通过每条走廊的时间。由于经验老到，他拿下一幅画需要5秒的时间。你的任务是编一个程序，计算在警察赶来之前，他最多能偷到多少幅画。

输入格式

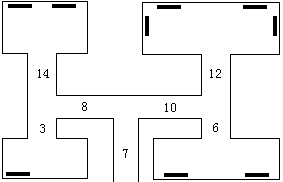
第一行是警察赶到的时间，以秒为单位。第 $2$ 行描述了艺术馆的结构，是一串非负整数，成对地出现：每一对的第一个数是走过一条走廊的时间，第 $2$ 个数是它末端的藏画数量；如果第 $2$ 个数是 $0$，那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出，请看样例。

一个展室最多有 $20$ 幅画。通过每个走廊的时间不超过 $20$ 秒。艺术馆最多有 $100$ 个展室。警察赶到的时间在 $6000$ 秒以内。

输出格式

输出最多能偷到的画的数量。

样例 #1

样例输入 #1

60
7 0 8 0 3 1 14 2 10 0 12 4 6 2

样例输出 #1

2

题解
首先想到，这个题的输入应该使用DFS读入，而不能用普通的读入方式。
读入方式十分新颖。
第二个坑点就是恰好偷完是不行的，因为警察已经来了。所以说M要-1的
第三个坑点就是走廊要走两遍，因为不可以穿墙。

考虑本题的思路是DP,重点是状态设计，我们要设计状态dp[i][j]为偷到第i个节点，恰好用了j分钟的最大画数。
那么对于一个节点u,如果这个节点是展厅，那么可以偷1到a[x]中的一些个 a[x]是此节点画的数量，但是现在的时间加上偷的时间的总和不能超过限定时间。

如果这个节点是走廊，考虑维护两个变量i,j。i代表在左展厅偷i分钟,j代表在右展厅偷j分钟。
限制条件就是i+当前时间<=限定时间 且 i+j+当前时间<=限定时间。
我们先遍历左右节点获取数据，然后合成这个状态的答案。注意别忘了加上左右节点的经过时间。

怎么合成呢，这就要用到树形背包
dp[x][tim+i+j]=max(dp[x][tim+i+j],dp[x2][tim+i]+dp[x2+1][tim+j]);

代码如下
int M,dp[605][605];
struct node{int v,c;}t[100001];
void read(int x){
cin>>t[x].v>>t[x].c;
t[x].v<<=1;
if(!t[x].c){
read(x2);
read(x2+1);
}

}
void dfs(int x,int tim){
if(t[x].c){
for(int i=1;i<=t[x].c&&tim+(i5)<=M;i){
int cnt=tim+(i5);
dp[x][cnt]=dp[x][cnt-5]+1;//利用上一次的答案
}
}else{
dfs(x2,tim+t[x2].v);
dfs(x2+1,tim+t[x*2+1].v);//加上左右节点的时间
for(int i=0;i+tim<=M;i){
for(int j=0;i+j+tim<=M;j++){
dp[x][tim+i+j]=max(dp[x][tim+i+j],dp[x2][tim+i]+dp[x*2+1][tim+j]);
}
}
}
}
int main(){
cin>>M;
M–;
read(1);
dfs(1,t[1].v);//首先要经过第一个
cout<<dp[1][M];
return 0;
}