P4281 [AHOI2008] 紧急集合 / 聚会

题目描述

欢乐岛上有个非常好玩的游戏，叫做“紧急集合”。在岛上分散有 $n$ 个等待点，有 $n-1$ 条道路连接着它们，每一条道路都连接某两个等待点，且通过这些道路可以走遍所有的等待点，通过道路从一个点到另一个点要花费一个游戏币。

参加游戏的人三人一组，开始的时候，所有人员均任意分散在各个等待点上（每个点同时允许多个人等待），每个人均带有足够多的游戏币（用于支付使用道路的花费）、地图（标明等待点之间道路连接的情况）以及对话机（用于和同组的成员联系）。当集合号吹响后，每组成员之间迅速联系，了解到自己组所有成员所在的等待点后，迅速在 $n$ 个等待点中确定一个集结点，组内所有成员将在该集合点集合，集合所用花费最少的组将是游戏的赢家。

小可可和他的朋友邀请你一起参加这个游戏，由你来选择集合点，聪明的你能够完成这个任务，帮助小可可赢得游戏吗？

输入格式

第一行两个正整数 $n$ 和 $m$，分别表示等待点的个数（等待点也从 $1$ 到 $n$ 进行编号）和获奖所需要完成集合的次数。

随后 $n-1$ 行，每行两个正整数 $a,b$，表示编号为 $a$ 和编号为 $b$ 的等待点之间有一条路。

随后 $m$ 行，每行用三个正整数 $x,y,z$，表示某次集合前小可可、小可可的朋友以及你所在等待点的编号。

输出格式

输出共 $m$ 行，每行两个用空格隔开的整数 $p,c$。其中第 $i$ 行表示第 $i$ 次集合点选择在编号为 $p$ 的等待点，集合总共的花费是 $c$ 个游戏币。

样例 #1

样例输入 #1

6 4  
1 2  
2 3  
2 4 
4 5
5 6
4 5 6
6 3 1
2 4 4 
6 6 6

样例输出 #1

5 2
2 5
4 1
6 0

提示

对于 $40\%$ 的数据，$n\leq2\times10^3$，$m\leq2\times 10^3$。

对于 $100\%$ 的数据，$1\leq x,y,z\leq n\leq 5\times10^5$，$1\leq m\leq 5\times 10^5$。

分析：
题目抽象出来的模型就是求三个点的lca

对于三个点，由于三个点的地位相同，所以下面仅讨论一种情况
dis(a,b)表示两点间的最短距离

1. 图上三个点在一条链上
   
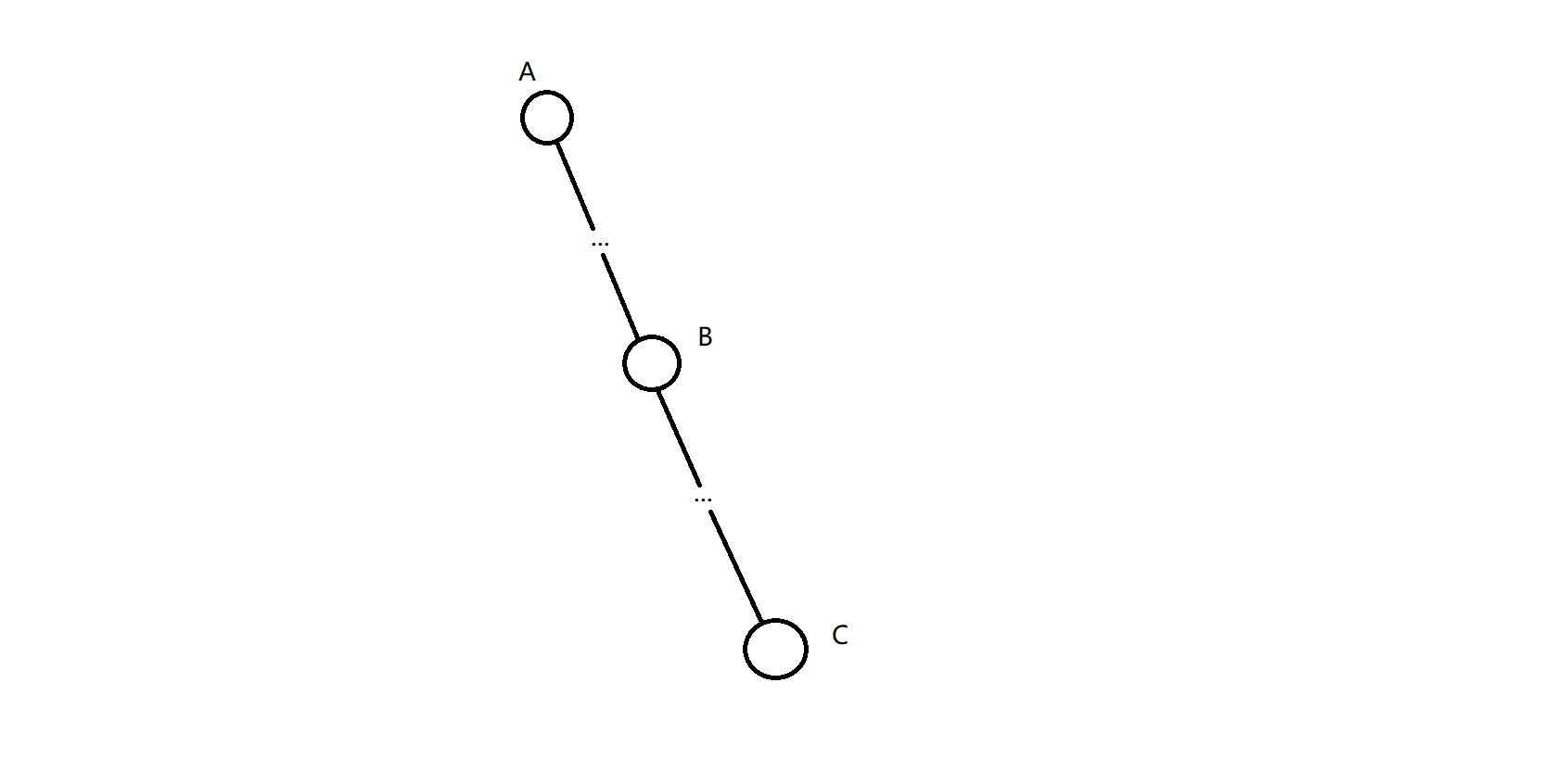
   通过比对我们发现最小值一定在B点上
   所以ans = dis(a,b)+dis(b,c);
2. 图上只有两个点在一条链上
   
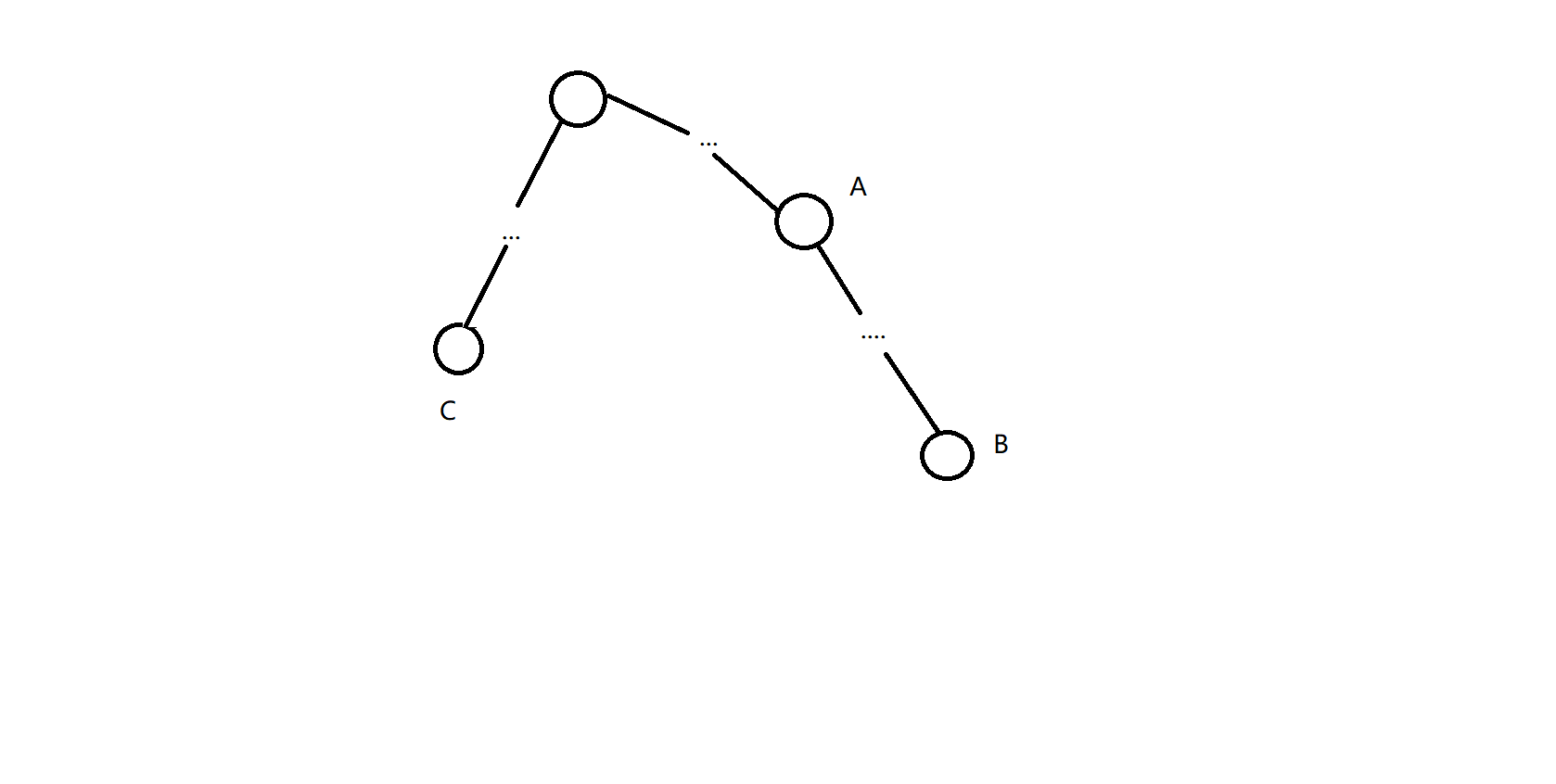
   对于这种情况我们考虑：先将一条链上的点合并成一个点，再走合成点和第三个点的最短路
   ans = dis(a,b)+dis(lcaAB,c);
3. 图上三个点都不在链上
   
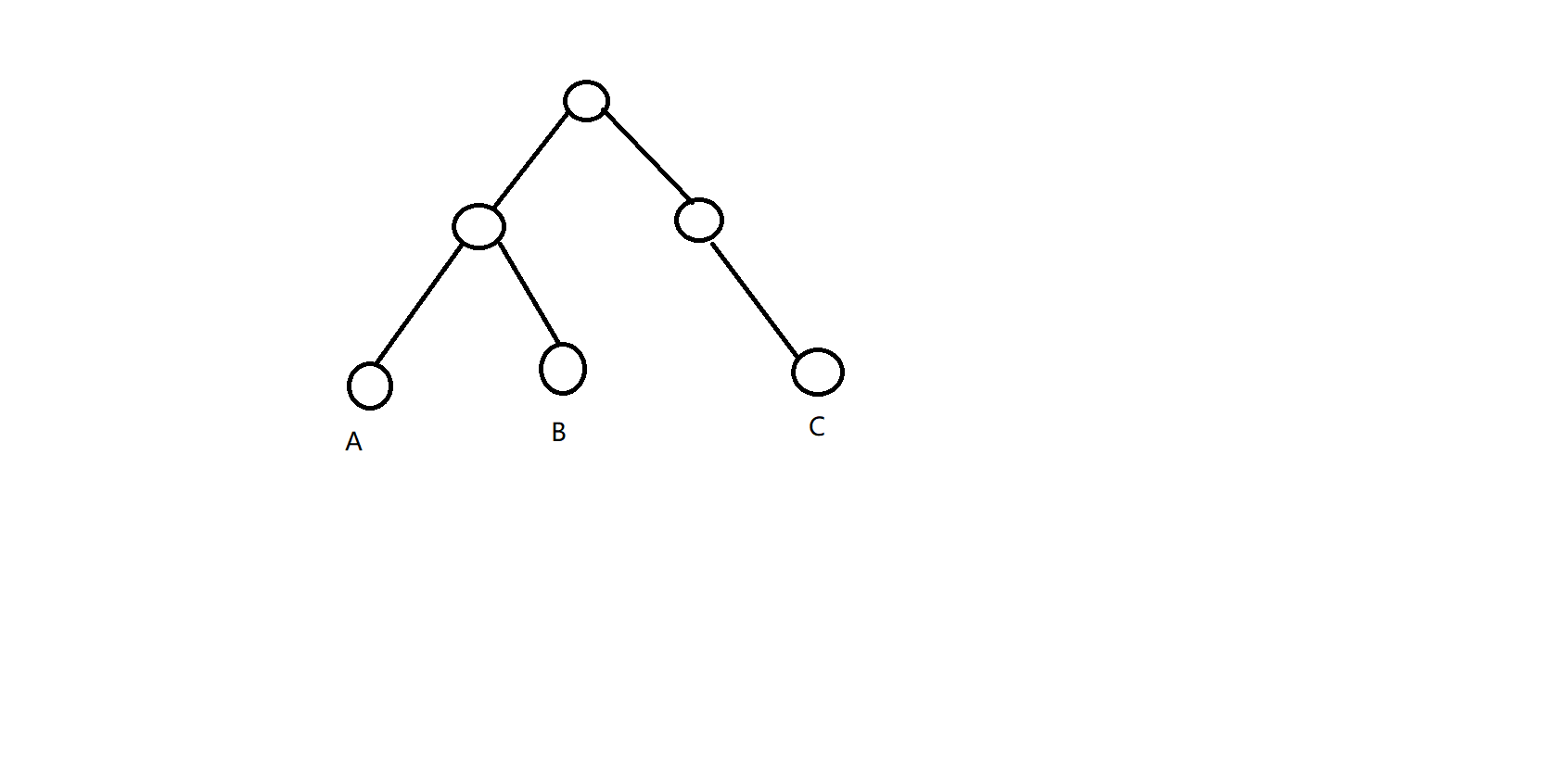
   我们只能枚举每种情况
   ans = min(dis(a,b)+dis(lcaAB,c),dis(a,c)+dis(lcaAC,b),dis(b,c)+dis(lcaBC,a));

总结
写代码时发现，第三种情况能把第一第二种都包括了，所以在写的时候只需要写第三种即可

代码：

#include <bits/stdc++.h>

const int N = 500010,M = 2*N;

using namespace std;

int h[N],e[M],ne[M],idx = 0;
int depth[N],fa[N][20];
int n,m,INF = 0x3f3f3f3f;

void add(int a,int b){
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}
int lca(int a,int b){
    if(depth[a]<depth[b]){
        int c = a;
        a = b;
        b = c;
    }
    for(int k = 19;k>=0;k--)
        if(depth[fa[a][k]]>=depth[b])
            a = fa[a][k];

    if(a == b) return a;
    for(int k = 19;k>=0;k--)
        if(fa[a][k]!=fa[b][k]){
            a = fa[a][k];
            b = fa[b][k];
        }
    return fa[a][0];
}
int dis(int a,int b){
    return depth[a]+depth[b]-2*depth[lca(a,b)];
}
void bfs(){
    depth[0] = 0;
    depth[1] = 1;
    int q[N];
    int hh = 0,tt = -1;
    q[++tt] = 1;
    while(tt>=hh){
        int t = q[hh++];
        for(int i = h[t];i!=-1;i = ne[i]){
            int j = e[i];
            if(depth[j] == 0){
                depth[j] = depth[t]+1;
                q[++tt] = j;
                fa[j][0] = t;
                for(int k = 1;k<=19;k++)
                    fa[j][k] = fa[fa[j][k-1]][k-1];
            }
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    memset(h,-1,sizeof h);
    for(int i = 1;i<=n-1;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
        add(b,a);
    }

    bfs();

    for(int i = 1;i<=m;i++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        int lcaAB = lca(a,b),lcaAC = lca(a,c),
        lcaBC = lca(b,c);
        int ans = INF,node = -1;
        int x0 = dis(a,b)+dis(lcaAB,c);
        int x1 = dis(a,c)+dis(lcaAC,b);
        int x2 = dis(b,c)+dis(lcaBC,a);
        if(ans>x0){
            ans = x0;
            node = lcaAB;
        }
        if(ans>x1){
            ans = x1;
            node = lcaAC;
        }
        if(ans>x2){
            ans = x2;
            node = lcaBC;
        }
        printf("%d %d\n",node,ans);
    }
}