历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

cht讲算法——堆

作者：

cht , 2020-08-21 21:03:00 , 所有人可见 , 阅读 1019

11

7

堆

补个漏hh。

1、堆是蛤

1-1 当二叉树变的有序时

堆，是一颗有序的二叉树

树大家总知道8。

那二叉树就是每个分叉都只有两个叉。

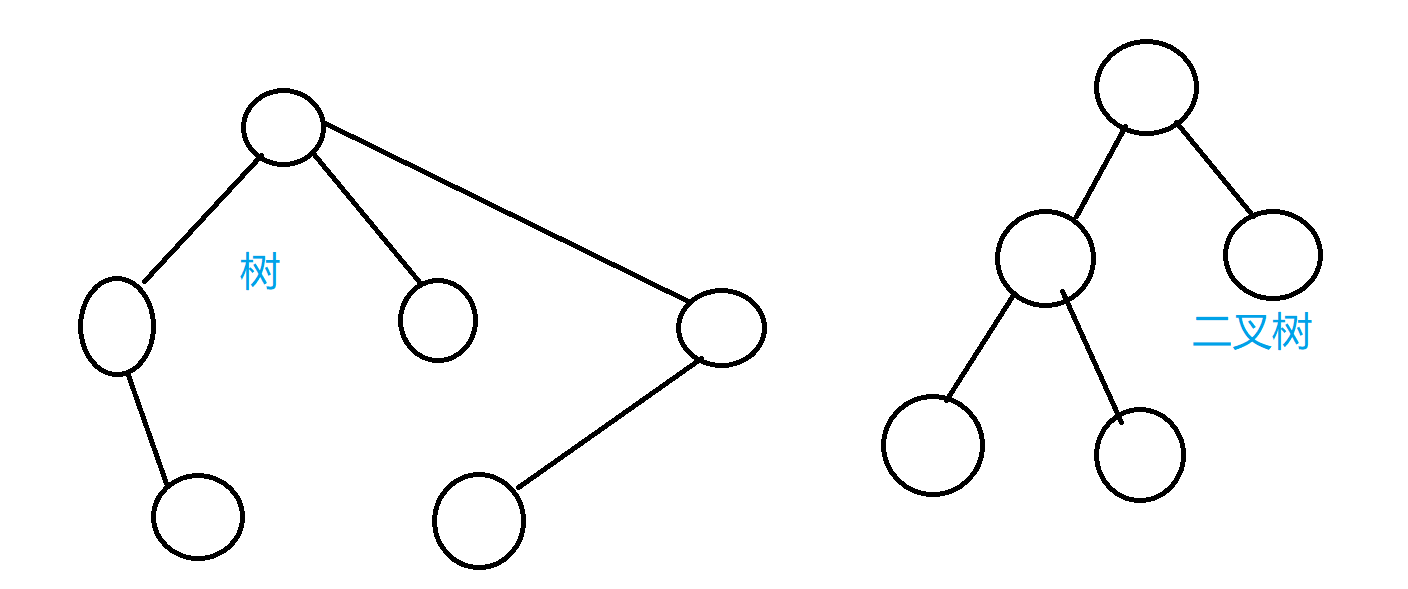
批注 2020-08-19 152649.png

加上数值后，一些强迫症患者发现很难看。

所以他们决定改一下上面的数字。

这个1，最好放在最上面吧qwq

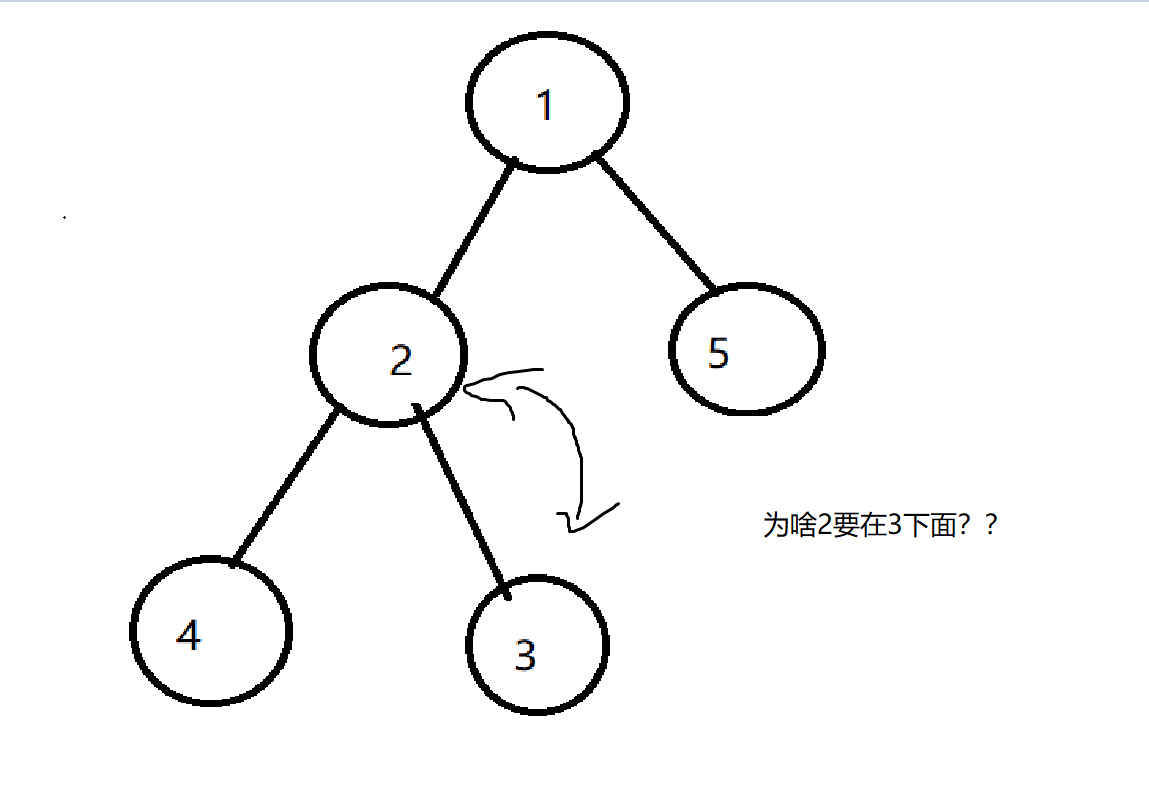
批注 2020-08-19 183146.png

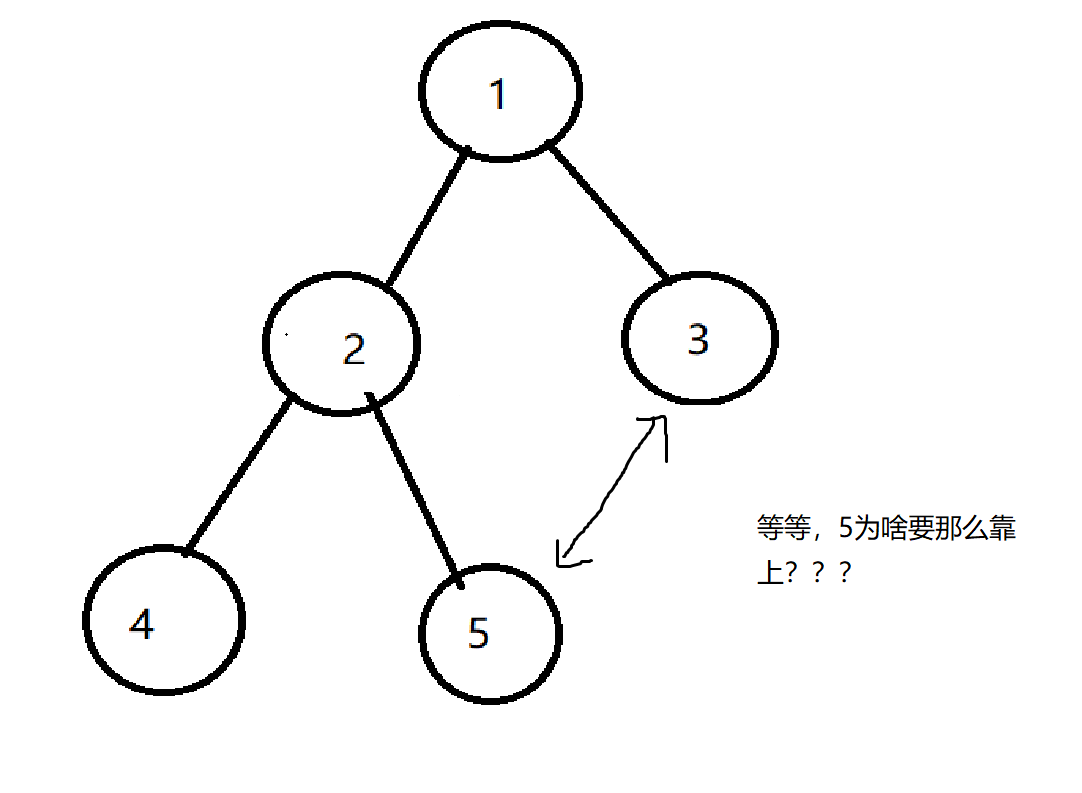
批注 2020-08-19 183422.png

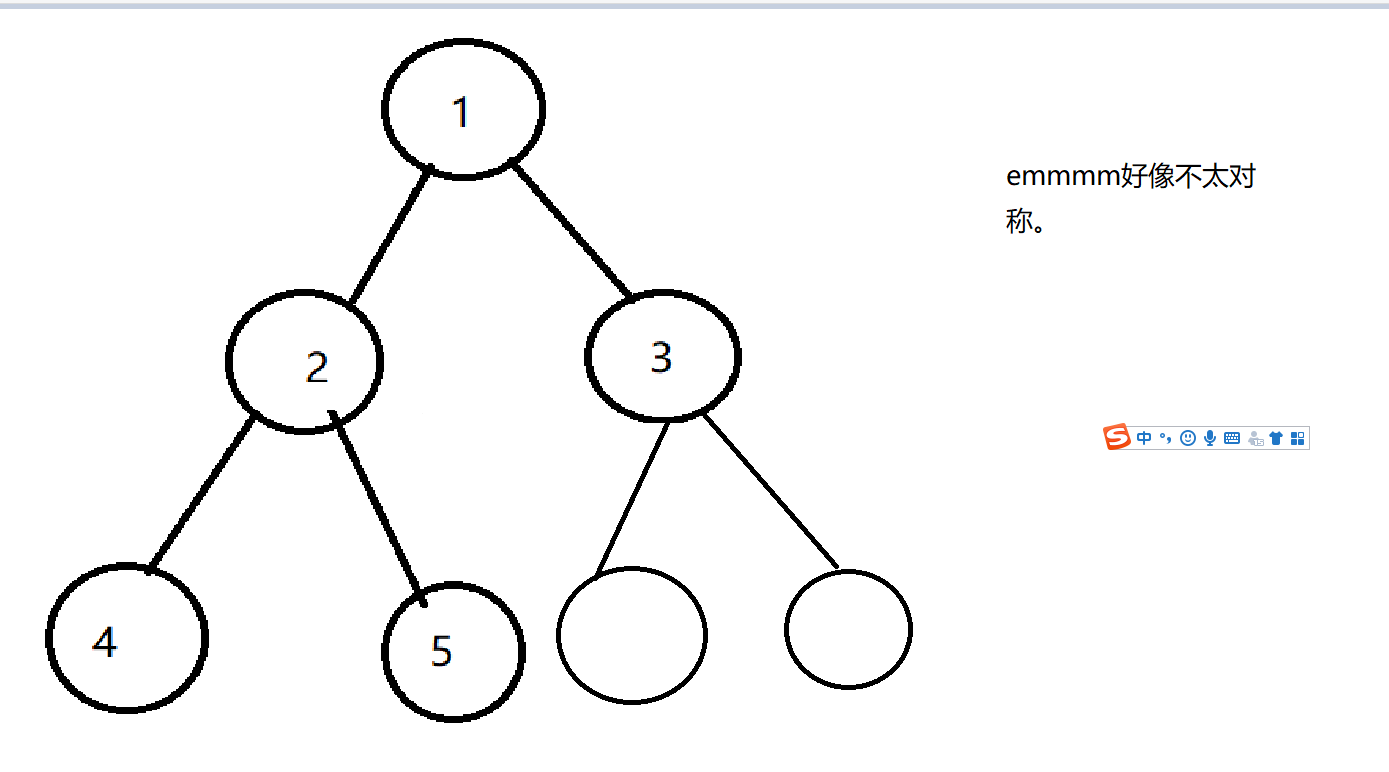
批注 2020-08-19 183317.png

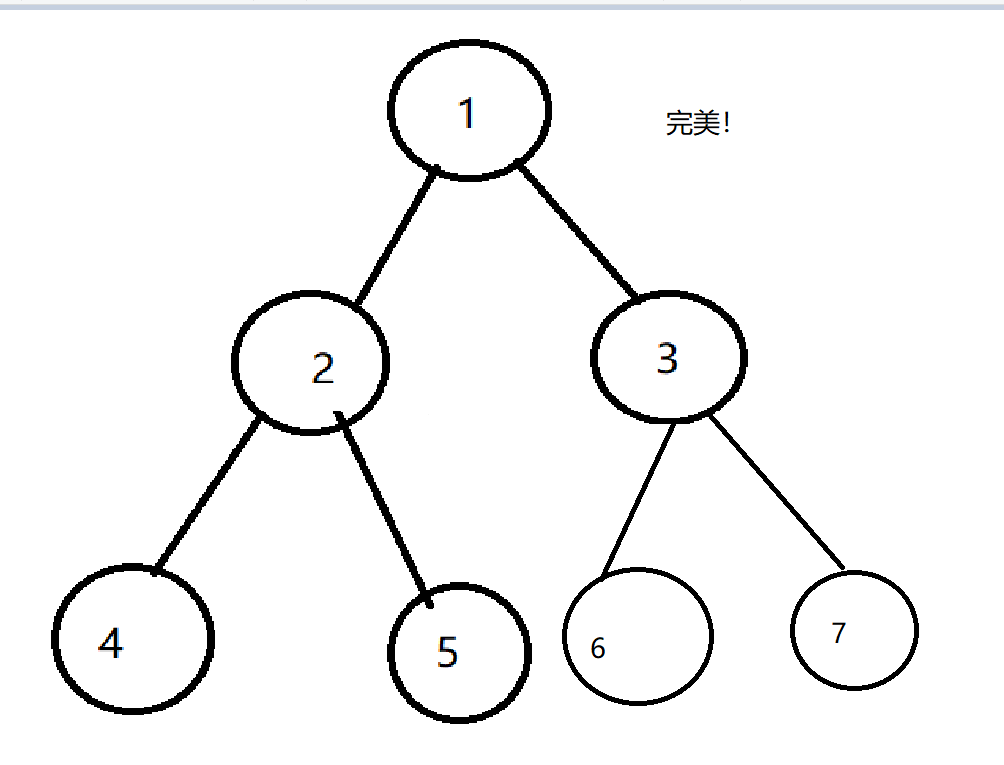
批注 2020-08-19 183455.png

于是，堆诞生了。

当然，堆也可以不对称啊~

1-2 堆的性质

咱们这里谈小根堆。

小根堆的性质是：约小的元素越靠上。

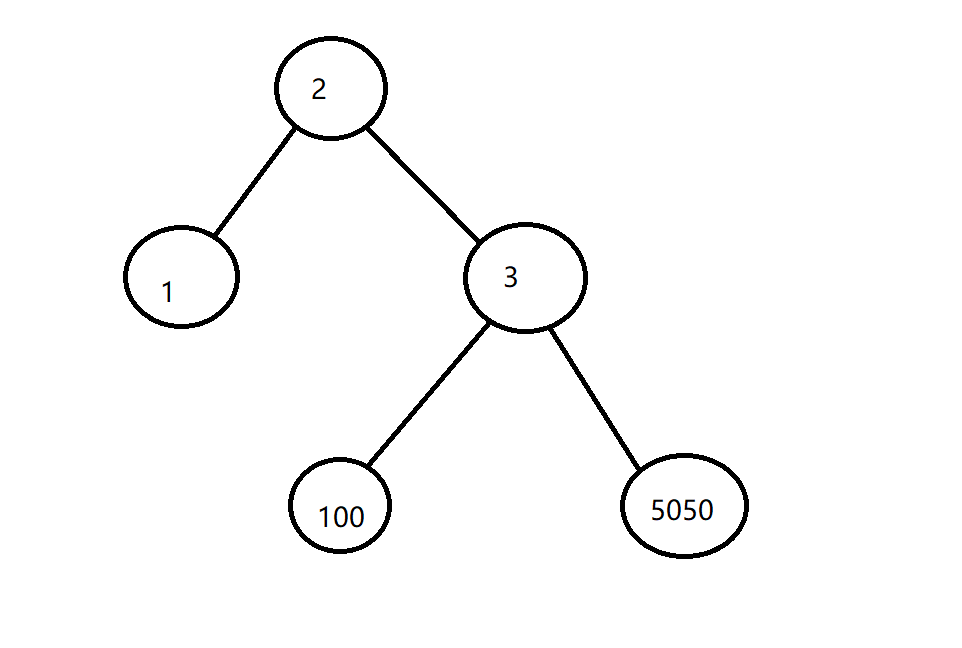
批注 2020-08-19 184242.png

这就不是。

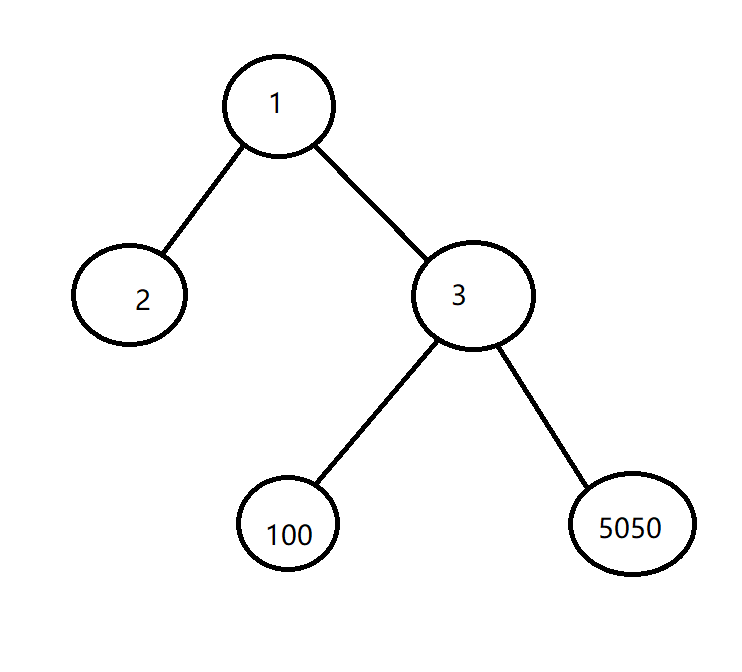
批注 2020-08-19 184312.png

这就是。

1-3 小根堆与大根堆

大根堆和小根堆只有一个区别：

一个从大到小，一个从小到大

就是这样。

2 堆的实现

2-1 STL实现堆

堆，是第一个数据结构的卡（线段树是第二个）

堆，不管STL还是手动实现都巨难写……（STL还好吧……

我们先来说STL实现。

c++中，有一个东西叫做优先队列。

priority_queue<int> heap;//!!!!

上面就是大根堆的定义。

priority_queue<int, vector<int>, greater<int>> heap;

这就是小根堆的定义。
当然，有时候定义是一个代码里最大的毒瘤。。。

priority_queue<pair<string, pair<int, vector<list<queue<int>>>>>, vector<pair<string, pair<int, vector<list<queue<int>>>>>>, greater<pair<string, pair<int, vector<list<queue<int>>>>>>> heap;

不过这个还是很好的，支持一些很不错的操作。

比如大家还记得堆优化Dijkstra？

就是用的这个。

简单列举几个操作：

priority_queue<int, vector<int>, greater<int>> heap;//定义一个堆
heap.top();//返回堆顶元素
heap.push(1);//向堆插入一个数。
heap.pop();//弹出堆顶元素
heap.empty();//判断堆是否为空
heap.size();//返回元素个数

注意，优先队列自动排序（sto

2-2 模拟堆

先看看题目：

维护一个集合，初始时集合为空，支持如下几种操作：

“I x”，插入一个数x；
“PM”，输出当前集合中的最小值；
“DM”，删除当前集合中的最小值（数据保证此时的最小值唯一）；
“D k”，删除第k个插入的数；
“C k x”，修改第k个插入的数，将其变为x；

现在要进行$N$次操作，对于所有第2个操作，输出当前集合的最小值。

输入格式
第一行包含整数$N$。

接下来$N$行，每行包含一个操作指令，操作指令为”I x”，”PM”，”DM”，”D k”或”C k x”中的一种。

输出格式
对于每个输出指令“PM”，输出一个结果，表示当前集合中的最小值。

每个结果占一行。

数据范围
$$ 1≤N≤10^5\\\ −10^9≤x≤10^9 $$
数据保证合法。

输入样例：

8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM

输出样例：

-10
6

$STL$我们只能写出钱3中操作。

于是我们发现了一个重要的问题：我们需要手写堆才能过掉这个题！

扫一眼题，是读入的数，所以我们需要建立一个映射：

hp:堆中点的插入次序
ph:每个插入的数所对应的下标

那么我们一个个想接下来5个操作。

插入操作

首先需要用$m$记录输入的数。

首先建立映射：

cnt ++;//堆的个数++
m ++;//输入的数++
h[cnt] = x;//把数放进堆，这时先不考虑维护堆的有序
hp[cnt] = m, ph[m] = cnt;//维护映射
up(cnt);//刚刚插入在了堆底，要把这个网上走。

查询操作

这个最简单，既然我们维护了堆，直接输出堆顶即可。

cout << h[1] << endl;

删除堆顶操作

这里就比较绕了，我们没有办法直接删除，但我们可以曲线救国：

交换堆顶和堆底
把堆底删除（即原来的堆顶）
把堆顶down一遍维护堆的有序

heap_swap(1, cnt);//注意维护映射，不能使用传统的交换
cnt --;//第二步，删除堆底
down(1);//维护堆的有序

删除任意位置操作

跟刚才的删除堆顶差不多。

找到k在堆中的位置
交换k的位置和堆底
删除堆底
维护堆的有序

k = ph[k];//找到，这里为了方便直接把k赋值成ph[k]
heap_swap(k, cnt);//交换
cnt --;//删除堆底
//此时，我们整个堆是无序是。
//如果只down的话，不行
//只up也不行
//所以不妨两个都做一遍即可
up(k);
down(k);

修改操作

几乎和上面的一模一样。

找到在堆中的位置
h[k] = x
up(k), down(k);

k = ph[k];
h[k] = x;
up(k);
dpwn(k);

`heap_swap`堆交换操作

交换ph，但得找到ph的位置
交换hp
交换h

void heap_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]);
    swap(h[a], h[b]);
}

`down`下降操作

就是一溜烟的判断。

void down(int u)
{
    int t = u;//注意，这里需要一个t来保存
    if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;//如果可以往左：记录
    if(u * 2 + 1<= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//如果可以往右，记录
    if(u != t)//判断是否移动
    {
        head_swap(u, t);
        down(t);//继续
    }
}

`up`操作

递归实现最香了。

~~哎哎别打我啊，爆栈是你们的事。。。~~

void up(int u)
{
    while(u / 2 && h[u] < h[u / 2])//疯狂试探可不可以上移
    {
        head_swap(u, u / 2);//如果可以就上移
        u >>= 1;
    }
}

完整代码

~~终于到了~~

#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
int h[N],ph[N],hp[N],cnt;
void head_swap(int a, int b)
{
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a],hp[b]);
    swap(h[a],h[b]);
}
void down(int u)
{
    int t=u;
    if(u * 2 <= cnt && h[u*2]<h[t]) t=u*2;
    if(u*2 + 1<= cnt && h[u * 2 + 1] < h[t]) t=u*2 + 1;
    if(u != t)
    {
        head_swap(u,t);
        down(t);
    }
}
void up(int u)
{
    while(u/2 && h[u] < h[u/2])
    {
        head_swap(u,u/2);
        u >>= 1;
    }
}
int main()
{
    int n,m=0;
    cin >> n;
    while(n--)
    {
        char op[5];
        int k,x;
        cin >> op;
        if(!strcmp(op, "I"))
        {
            cin >> x;
            cnt ++ ;
            m ++ ;
            ph[m] = cnt, hp[cnt] = m;
            h[cnt] = x;
            up(cnt);
        }
        else if(!strcmp(op, "PM"))
        {
            cout << h[1] << endl;
        }
        else if(!strcmp(op, "DM"))
        {
            head_swap(1, cnt);
            cnt -- ;
            down(1);
        }
        else if(!strcmp(op, "D"))
        {
            cin >> k;
            k = ph[k];
            head_swap(k, cnt);
            cnt -- ;
            up(k);
            down(k);
        }
        else{
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            up(k);
            down(k);
        }
    }
}

作者：cht
链接：https://www.acwing.com/activity/content/code/content/339836/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

复制的原来代码，码风一般，大家见谅hh

3、堆的应用

3-1、堆排序

堆排序可以抽出前m个最小的数。
可以利用堆的性质，维护有序，我们需要实现以下这些操作：

初始化堆
删除堆顶
查询堆顶

基本过程如下：

读入
初始化堆
做m次
每次取出堆顶
删除堆顶
维护堆的有序

读入

一行cin上西天青天。

cin >> n >> m;
for(int i = 1; i <= n; i ++) cin >> h[i];

初始化

把从$n \div 2$开始的所有数$down$一遍。

为啥呢？

从$n \div 2$是n的下一层，然后每次模拟插入的过程，把这个数下沉维护堆的有序。

cnt = n;//落单的来了
for(int i = n / 2; i; i --) down(i);

剩下的一锅端

while(m --)
{
    cout << h[1] << ' ';
    h[1] = h[cnt];
    cnt --;
    down(1);
}

$down$操作上面有了，这里就不浪费笔墨了。

完整代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, h[N], cnt;
void down(int u)
{
    int t = u;
    if(u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;
    if(u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
    if(t != u)
    {
        swap(h[t], h[u]);
        down(t);
    }
}
int main()
{
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; i ++) cin >> h[i];
    cnt = n;
    for(int i = n / 2; i; i --) down(i);
    while(m --)
    {
        cout << h[1] << ' ';
        h[1] = h[cnt];
        cnt --;
        down(1);
    }
    return 0;//我默默的加上了这句话
}

作者：cht
链接：https://www.acwing.com/activity/content/code/content/335992/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。