例题:简单题
1.AcWing 745. 数组的右上半部分
刚开始的思路:
#include<iostream>
using namespace std;
int main()
{
char c;
float M[12][12],sum=0;
cin>>c;
int cnt=0;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j){
cin>>M[i][j];
if(j>i){
sum+=M[i][j];
cnt++;//求右上半部分有多少个数
}
}
if(c=='S') printf("%.1f",sum);
else printf("%.1f",sum/cnt);
return 0;
}
another:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char ch;
double M[12][12];
double sum=0;
int cnt=0;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
for(int i=0;i<12;++i)
for(int j=i+1;j<12;++j){
sum+=M[i][j];
cnt++;
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
第一个思路是找到了右上部分坐标的规律,i>j。但是这个思路不具普遍性。第二个思路是找每行第一个绿色的横坐标与行数的关系。

2.AcWing 747. 数组的左上半部分
刚开始的思路:
#include<iostream>
using namespace std;
int main()
{
char c;
double M[12][12],sum=0;
cin>>c;
int cnt=0;
for(int i=0;i<12;++i){
for(int j=0;j<12;++j){
cin>>M[i][j];
if(j<12-i-1){
sum+=M[i][j];
cnt++;
}
}
}
if(c=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
anther:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char ch;
double M[12][12];
double sum=0;
int cnt=0;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
for(int i=0;i<12;++i)
for(int j=0;j<11-i;++j){
sum+=M[i][j];
cnt++;
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
相比来说,第二个更加简单一点。
3.AcWing 749. 数组的上方区域
刚开始的思路:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char c;
float M[12][12],sum=0;
int cnt=0;
cin>>c;
for(int i=0;i<12;i++)
for(int j=0;j<12;j++){
cin>>M[i][j];
if(i<5&&j<12-i-1&&j>i){
sum+=M[i][j];
cnt++;
}
}
if(c=='S') printf("%.1f",sum);
else printf("%.1f",sum/cnt);
return 0;
}
another:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char ch;
double M[12][12];
double sum=0;
int cnt=0;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
for(int i=0;i<5;++i)
for(int j=i+1;j<11-i;++j){
sum+=M[i][j];
cnt++;
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
相比来说还是思路二简单,而且不易出错。
4.AcWing 751. 数组的左方区域
刚开始的思路:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char c;
float M[12][12],sum=0;
int cnt=0;
cin>>c;
for(int i=0;i<12;i++)
for(int j=0;j<12;j++){
cin>>M[i][j];
if(i>0&&i<=5&&j<=i){
sum+=M[i][j];
cnt++;
}
if(i>5&&i<11&&j<12-i){
sum+=M[i][j];
cnt++;
}
}
if(c=='S') printf("%.1f",sum);
else printf("%.1f",sum/cnt);
return 0;
}
another:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
char ch;
double M[12][12];
double sum=0;
int cnt=0;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
for(int i=1;i<=5;++i)
for(int j=0;j<i;++j){
sum+=M[i][j];
cnt++;
}
for(int i=6;i<=10;++i)
for(int j=0;j<11-i;++j){
sum+=M[i][j];
cnt++;
} //这次和前面不一样,分成了两步。
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
5. AcWing 748. 数组的右下半部分
刚开始的思路:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
double M[12][12];
char ch;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
double sum=0,cnt=0;
for(int i=1;i<=11;++i)
for(int j=12-i;j<=11;++j){
cnt++;
sum+=M[i][j];
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
6. AcWing 746. 数组的左下半部分
刚开始的思路:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
double M[12][12];
char ch;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
double sum=0,cnt=0;
for(int i=1;i<=11;++i)
for(int j=0;j<i;++j){
cnt++;
sum+=M[i][j];
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
7. AcWing 750. 数组的下方区域
刚开始的思路:
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
double M[12][12];
char ch;
cin>>ch;
for(int i=0;i<12;++i)
for(int j=0;j<12;++j)
cin>>M[i][j];
double sum=0,cnt=0;
for(int i=7;i<12;++i)
for(int j=12-i;j<=i-1;++j){
cnt++;
sum+=M[i][j];
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
8. AcWing 752. 数组的右方区域
#include<iostream>
#include<cstdio>
using namespace std;
int main()
{
double M[12][12];
char ch;
cin>>ch;
for(int i=0;i<12;i++)
for(int j=0;j<12;++j)
cin>>M[i][j];
double sum=0,cnt=0;
for(int i=1;i<=5;++i)
for(int j=12-i;j<=11;j++){
cnt++;
sum+=M[i][j];
}
for(int i=6;i<=10;i++)
for(int j=i+1;j<=11;++j){
cnt++;
sum+=M[i][j];
}
if(ch=='S') printf("%.1lf",sum);
else printf("%.1lf",sum/cnt);
return 0;
}
例题:困难题
1. AcWing 753. 平方矩阵 I

#include<iostream>
using namespace std;
int main()
{
int n,upon,under,left,right;
int N[110][110];
while(cin>>n,n>0){
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j){
upon=i;
under=n-i+1;
left=j;
right=n-j+1;
N[i][j]=min(min(upon,under),min(left,right));
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j)
cout<<N[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
#include<iostream>
using namespace std;
int main()
{
int n;
while(cin>>n,n){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
int up=i,down=n-i+1,left=j,right=n-j+1;
cout<<min(min(up,down),min(left,right))<<" ";
}
cout<<endl;
}
cout<<endl;
}
return 0;
}
此题其实不用开数组。
注意双重for循环的i和j要从1开始!!!
2. AcWing 754. 平方矩阵 II
这个题的规律不难发现:(1)对角线数值为1;(2)数值关于对角线对称;(3)每行从对角线数值开始逐个+1;
这样的话,我们就可以先将对角线上的数值初始为1,然后计算出对角线上方的部分(从对角线开始逐个+1),最后求对角线下方的部分(a[j][i]=a[i][j])
#include<iostream>
using namespace std;
int main()
{
int n;
int N[110][110];
while(cin>>n,n){
for(int i=1;i<=n;++i){
N[i][i]=1;
for(int j=i+1;j<=n;j++){
N[i][j]=N[i][j-1]+1;
N[j][i]=N[i][j];
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j)
cout<<N[i][j]<<" ";
cout<<endl;
}
cout<<endl;
}
return 0;
}
another:
#include<iostream>
using namespace std;
int q[100][100];
int main()
{
int n;
while(cin >> n, n){
for(int i=0; i<n; ++i)
{
q[i][i] = 1;
for(int j = i + 1, k = 2;j < n; ++j, ++k) q[i][j] = k;
for(int j = i + 1, k = 2;j < n; ++j, ++l) q[j][i] = k;
}
for(int i = 0; i < n; ++i )
{
for(int i = 0;i < n; ++i) cout << q[i][j] << " ";
cout << endl;
}
cout << endl;
}
return 0;
}
3. AcWing 756. 蛇形矩阵
刚开始没有思路,看了y总视频看了一半写出来的:
#include<iostream>
using namespace std;
int a[100][100];
bool b[100][100];
int main()
{
int n,m;
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};//下标一定要从1开始!!!!
cin>>n>>m;
int x=0,y=0,cnt=0;
for(int i=1;i<=n*m;++i){
a[x][y]=i;
b[x][y]=true;//填入数值的显示为true;
if((x+dx[cnt%4]==0)&&(y+dy[cnt%4]==m)||(x+dx[cnt%4]==n)&&(y+dy[cnt%4]==m-1)||(x+dx[cnt%4]==n-1)&&(y+dy[cnt%4]==-1)||b[x+dx[cnt%4]][y+dy[cnt%4]]==true)
cnt++; //这个cnt%4是个值得思考的地方,有点东西!!!!!
x=x+dx[cnt%4];
y=y+dy[cnt%4];//此操作是让下一个值接收i。
}
for(int i=0;i<n;++i){
for(int j=0;j<m;++j)
cout<<a[i][j]<<" ";
cout<<endl;
}
return 0;
}
感觉这个地方中cnt%4写的很有水平,嘿嘿嘿。忘记是在哪看到别人用到过,意识中就用上了.
下面说一下y总的完整思路:

#include<iostream>
using namespace std;
int res[100][100];//全局变量的初始值为零!!!
int main()
{
int n, m;
cin >> n >> m;
int dx[] = {0, 1, 0, -1}, dy[] = {1, 0, -1, 0};//下标一定要从1开始!!!!
for (int x = 0, y = 0, d = 0, k = 1; k <= n * m; ++k)//此处一些变量我都是在for之前定义的,y总都定义在括号内,这样看起来更简洁易懂。
{
res[x][y] = k;
int a = x + dx[d], b = y + dy[d];
if(a < 0 || a >= n || b < 0 || b >= m || res[a][b])//此处的res[a][b]和全局变量res[100][100]遥相呼应,因为全局变量的初始值为零,而局部变量的初始值不确定,所以此处未执行的变量为零,执行过的变量不为0;
{//上面的判断条件比我的更简洁,是我想复杂了.
d = (d + 1) % 4; //此处和我的原理其实一样,我的是先++,再放到数组中。
a = x + dx[d], b = y + dy[d];
}
x = a, y = b;
}
for(int i = 0; i < n; ++i)//注意此处是从零开始的!!!
{
for(int j = 0; j < m; j ++) cout << res[i][j] << " ";
cout << endl;
}
return 0;
}

后来又做这道题的时候,dx[]和dy[]数组是从下标1开始的,所以就一直运行出错,后来发现问题就出在这,应该从0开始,以后要注意,碰到要取模循环的时候下标一定要从0开始!!!!!
4.AcWing 螺旋折线 第九届蓝桥杯省赛C++B组
这个题第一眼做的时候脑中就觉着有些熟悉,一想不就是上边那道题吗,于是就按照上边的思路做,模拟,但是具体一想跟上边还不一样,蛇形矩阵那道题是从外到内,这个题是从内到外,这个要转向的条件不好想,想了好一会.

#include<iostream>
using namespace std;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1},dz[]={1,0,1,0};
int x,y;
int main()
{
int m=0,n=0;//表示每一次点的坐标
long long num=1;//表示sum达到这个数值就要转向
long long sum=0;//坐标每变化一次,sum++,当sum等于num的时候,表示要转向了
long long l=0;//l表示左 上 右 下 左 上 右 下...取模变化的值
long long k=0;//k表示1 1 2 2 3 3 4 4 5 5...取模变化的值
long long cnt=0;//表示dis(x,y)
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
cout<<cnt<<endl;
return 0;
}
写出来后回过头再来看这个题的切入点就是那个转向条件,什么时候转向,转向后哪些变量发生变化,这些搞明白后其他的就很简单了
调试了几个图上的点后满心欢喜的提交,却显示TLE,唉,一看没通过的样例,(498103014,945809204),这才发现这个题因为范围的原因不能用上面模拟这个思路.(吃饭的时候把TLE这个样例在Dev上跑了一下,跑了半个小时,x和y的值才刚刚过百…)
这个题既然不能用模拟来解决,那么就是有公式或者有规律了,观察了一下,还真发现了规律:(有图的题都要去画一下)
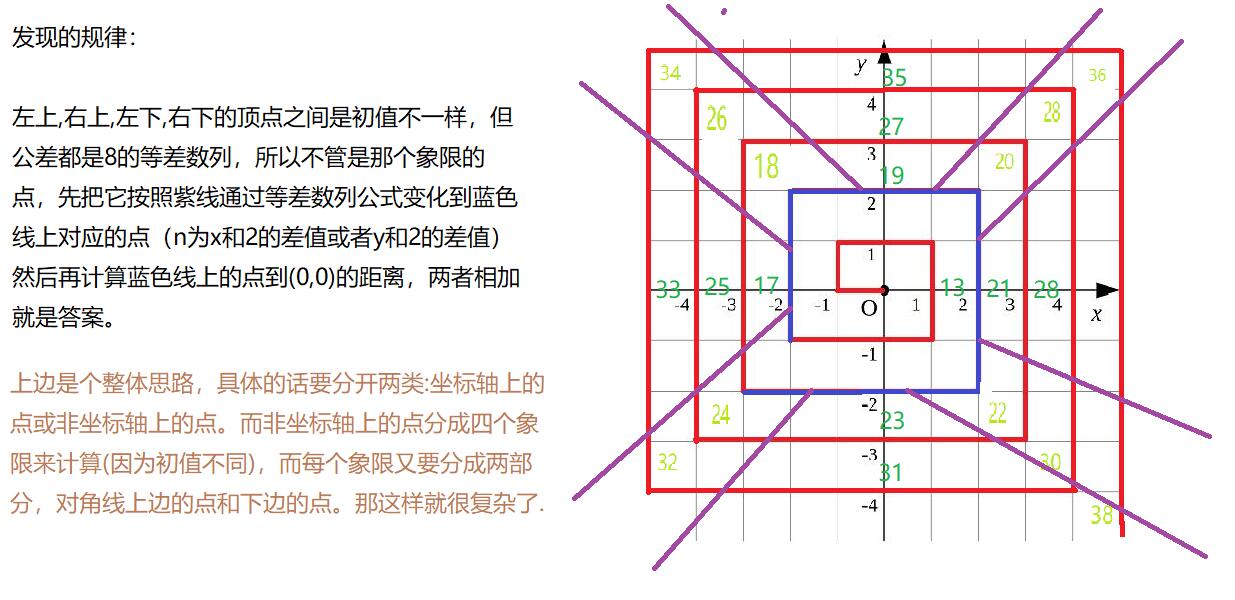
#include<iostream>
using namespace std;
int dx[]={-1,0,1,0},dy[]={0,1,0,-1},dz[]={1,0,1,0};
int x,y;
int main()
{
cin>>x>>y;
int m=0,n=0;//表示每一次点的坐标
long long num=1;//表示sum达到这个数值就要转向
long long sum=0;//坐标每变化一次,sum++,当sum等于num的时候,表示要转向了
long long l=0;//l表示dx,dy的值
long long k=0;//k表示1 1 2 2 3 3 4 4 5 5...取模变化的值
long long cnt=0;//表示dis(x,y)
if(abs(x)*abs(y)>6)
{
if(x==0)
{
if(y>0)
{
cnt=(y-2)*19+(y-2)*(y-3)*8/2;
x=0;y=2;
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
else
{
cnt=(abs(y)-2)*23+(abs(y)-2)*(abs(y)-3)*8/2;
x=0;y=-2;
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
}
else if(y==0)
{
if(x>0)
{
cnt=(x-2)*21+(x-2)*(x-3)*8/2;
x=2;y=0;
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
else
{
cnt=(abs(x)-2)*17+(abs(x)-2)*(abs(x)-3)*8/2;
x=-2;y=0;
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
}
else
{
if(x>0&&y>0)//第一象限
{
if(x>=y)//对角线之下
{
cnt=(x-2)*20+(x-2)*(x-3)*8/2;
y=y-(x-2);x=2;
}
else//对角线之上
{
cnt=(y-2)*20+(y-2)*(y-3)*8/2;
x=x-(y-2);y=2;
}
}
else if(x<0&&y>0)//第二象限
{
if(abs(x)>=abs(y))//对角线之下
{
cnt=(abs(x)-2)*18+(abs(x)-2)*(abs(x)-3)*8/2;
y=y-(abs(x)-2);x=-2;
}
else//对角线之上
{
cnt=(abs(y)-2)*18+(abs(y)-2)*(abs(y)-3)*8/2;
x=x+(y-2);y=2;
}
}
else if(x>0&&y<0)//第三象限
{
if(abs(x)>=abs(y))//对角线之上
{
cnt=(x-2)*22+(x-2)*(x-3)*8/2;
y=y+(x-2);x=2;
}
else//对角线之下
{
cnt=(abs(y)-2)*22+(abs(y)-2)*(abs(y)-3)*8/2;
x=x-(abs(y)-2);y=-2;
}
}
else{//第四象限
if(x>=y)//对角线之下
{
cnt=(abs(y)-2)*24+(abs(y)-2)*(abs(y)-3)*8/2;
x=x+(abs(y)-2);y=-2;
}
else//对角线之上
{
cnt=(abs(x)-3)*24+(abs(x)-3)*(abs(x)-4)*8/2;
y=y+(abs(x)-3);x=-3;
}
}
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
}
else
{
while(true)
{
if(m==x&&n==y) break;
m=m+dx[l%4];
n=n+dy[l%4];
//cout<<m<<" "<<n<<endl;
cnt++;
sum++;
if(sum==num){
l++;
k++;
num=num+dz[k%4];
sum=0;
}
}
}
cout<<cnt;
return 0;
}
//说实话上边这个代码写了一天...
四个象限运行样例都正确后提交还是显示超时,为什么会超时呢,按照上面的思路,以341238 572290为例,因为在对角线上方,首先要定位到横坐标为2,那么这个坐标就是(-231050,2),当时看到这个结果有点惊讶,想了一下明白了,之前试的样例都是太小了,这个x和y相差太大了,所以就去了别的象限,所以上边的思路还是有bug的,但是现在不用改上面的bug了,因为改完后就会定位到(231050,2)这个位置输入到while循环之中后还是会TLE.所以这个思路对x和y很大并且x和y的差值较大时不合适.
还有输入108 -2时输出的答案也不对,它是定位到了(2,104),和自己想的有出入。这也说明其实上边的思路有很大的问题.
冥冥之中感觉这个题肯定是围绕等差数列这个规律来计算的,只不过有些小细节上不对,既然定位到蓝线上后再运行还是会存在x或者y有可能很大的情况,那么这个先定位到蓝线上就不可取了.
通过观察,完全可以定位到0:
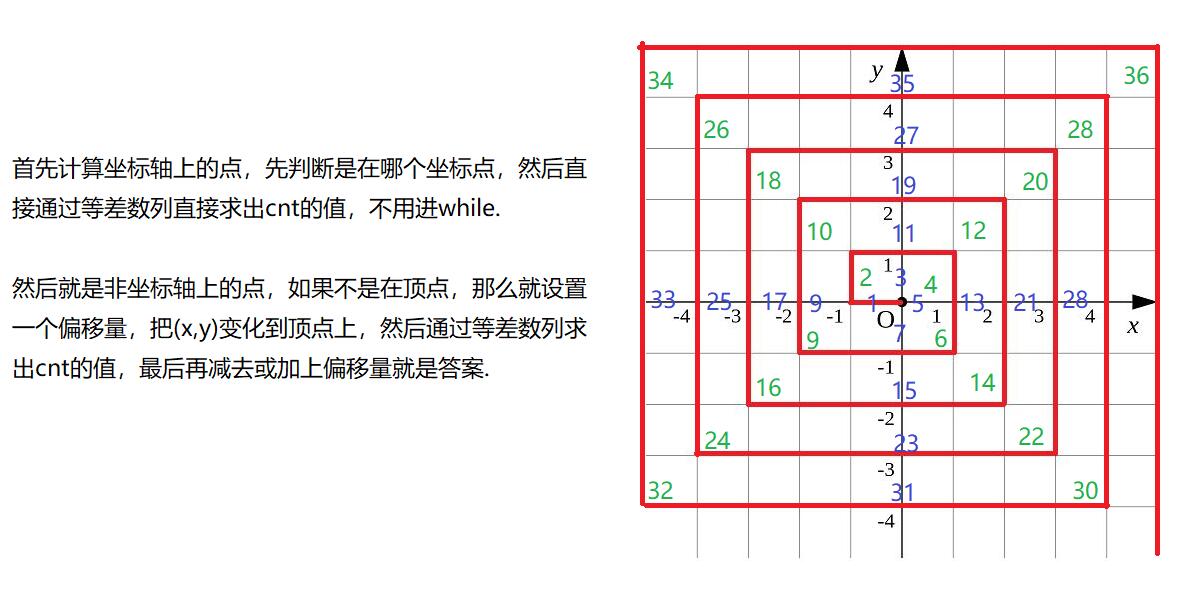
#include<iostream>
#include<math.h>
using namespace std;
int main()
{
long long x,y;
long long cnt=0,num;
cin>>x>>y;
if(x==0)
{
if(y>0)
cnt=y*3+y*(y-1)*8/2;
else
cnt=abs(y)*7+abs(y)*(abs(y)-1)*8/2;
}
else if(y==0)
{
if(x>0)
cnt=x*5+x*(x-1)*8/2;
else
cnt=abs(x)+abs(x)*(abs(x)-1)*8/2;
}
else
{
if(x>0&&y>0)//第一象限
{
if(x>y)//对角线下
{
num=x-y;//+
cnt=x*4+x*(x-1)*8/2+num;
}
else
{
num=x-y;//-
cnt=y*4+y*(y-1)*8/2+num;
}
}
else if(x<0&&y>0)//第二象限
{
if(abs(x)>y)//对角线下
{
num=x+y;//-
cnt=abs(x)*2+abs(x)*(abs(x)-1)*8/2+num;
}
else
{
num=x+y;//+
cnt=y*2+y*(y-1)*8/2+num;
}
}
else if(x>0&&y<0)//第四象限
{
if(x>=abs(y))//对角线上
{
num=abs(y)-x;//-
cnt=x*6+x*(x-1)*8/2+num;
}
else
{
num=abs(y)-x;//+
cnt=abs(y)*6+abs(y)*(abs(y)-1)*8/2+num;
}
}
else//第三象限
{
if(x<y)//线上
{
num=y-x-1;//+
cnt=(abs(x)-1)*8+(abs(x)-1)*(abs(x)-2)*8/2+num+1;
}
else
{
num=y-x-1;//-
//cout<<num<<endl;
cnt=abs(y)*8+abs(y)*(abs(y)-1)*8/2+num+1;
}
}
}
cout<<cnt<<endl;
return 0;
}
y总说这个模拟可以按照每一步来模拟,当然也可以按照每一行或者一列来模拟:
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long LL;
int main()
{
int x,y;
cin >> x >> y;
int dx[4]={0,1,0,-1},dy[4]={1,0,-1,0};
int a = 0,b = 0, dir = 3,step = 0;
LL distance = 0;
while(true)
{
int l = step / 2 + 1;
int c = a + dx[dir] * l,d = b + dy[dir]*l;
if(a ==c && a==x &&min(b,d) <=y && man(b,d) >=y)
{
cout << distance + abs(y - b) << endl;
break;
}
if(b ==d && b == y && min(a,c) <= x && max(a,c) >=x)
{
cout << distance + abs(x - a) << endl;
break;
}
distance += l;
dir = (dir + 1) % 4,step ++;
a = c,b = d;
}
return 0;
}
下面来看一下y总的规律做法:

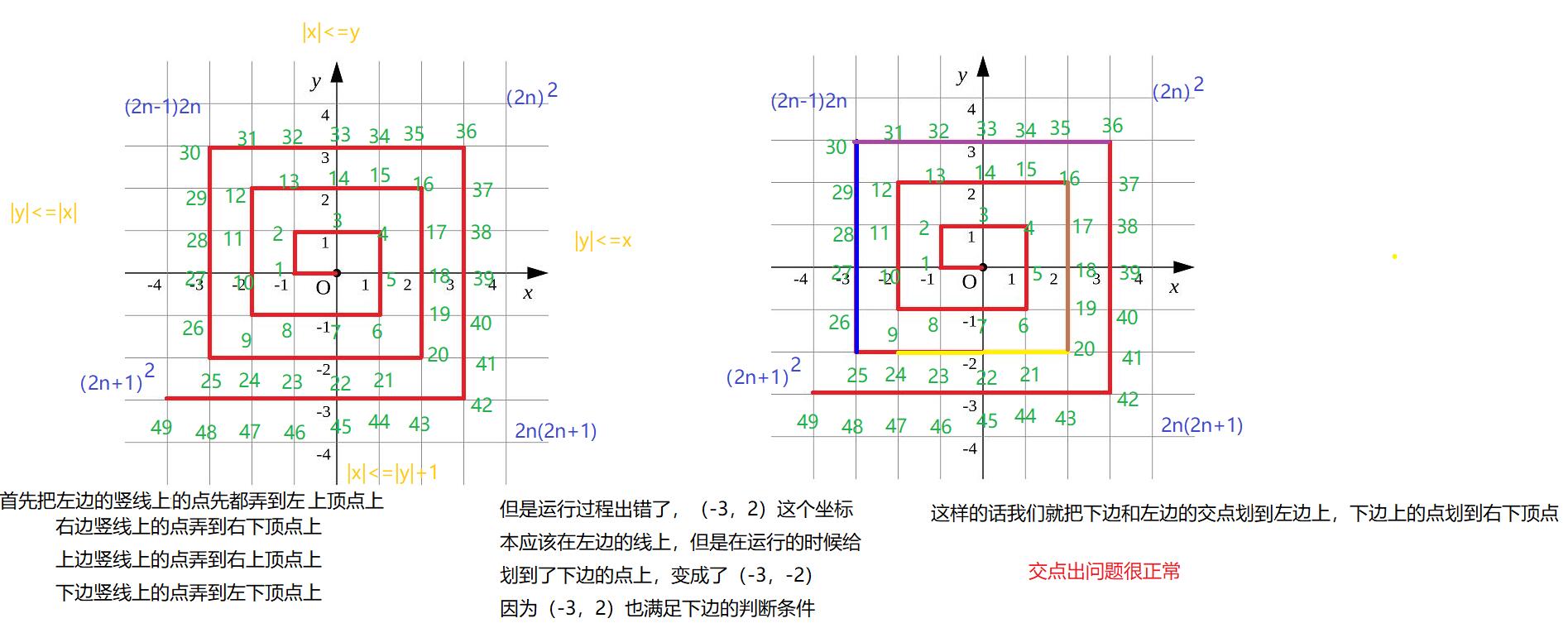
#include<iostream>
#include<math.h>
using namespace std;
int main()
{
long long x,y;
long long cnt=0,num;
cin>>x>>y;
if(abs(x)<=y)//上
{
num=y-x;
cnt=2*y*2*y-num;
}
else if(abs(y)<=x)//右边
{
num=abs(0-x-y);
cnt=2*x*(2*x+1)-num;
}
else if(abs(x)<abs(y)+1)//下边
{
num=abs(y)-x;
cnt=(2*abs(y))*(2*abs(y)+1)+num;
}
else//左边
{
num=abs(x)-y;
cnt=(2*abs(x)-1)*2*abs(x)-num;
}
cout<<cnt<<endl;
return 0;
}
上边是听了y总的思路自己写的代码
下面是y总的代码:
#include<iostream>
using namespace std;
typedef long long LL;
int main()
{
int x,y;
cin>>x>>y;
if(abs(x)<=y)//在上方
{
int n=y;
cout<<(LL)(2*n-1)*(2*n)+x-(-n)<<endl;
}
else if(abs(y)<=x)//在右方
{
int n=x;
cout<<(LL)(2*n)*(2*n)+n-y<<endl;
}
else if(abs(x)<=abs(y)+1 && y<0)//在下方
{
int n=abs(y);
cout<<(LL)(2*n)*(2*n+1)+n-x<<endl;
}
else//在左方
{
int n=abs(x);
cout<<(LL)(2*n-1)*(2*n-1)+y-(-n+1)<<endl;
}
return 0;
}
//y总上边到左上顶点,右边到右上顶点,下边到右下顶点,左边到左下顶点
总结:


