$\huge{线段树合并}$

将两颗权值线段树合并的操作，被称为线段树合并。

合并时对应位置上的权值相加，如下图所示。

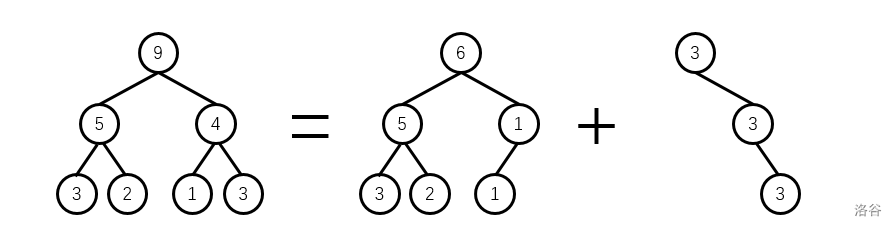
将两颗满二叉树合并，复杂度必然是 $O(n \log n)$ 。

如果现有 $n$ 颗动态开点权值线段树，这些线段树上最多有 $m$ 种不同的权值。

代码实现如下：

int merge(int x, int y, int l, int r) {
    if (!x || !y) return x + y;
    if (l == r) return x;
    int mid = l + r >> 1;
    tr[x].l = merge(tr[x].l, tr[y].l, l, mid);
    tr[x].r = merge(tr[x].r, tr[y].r, mid + 1, r);
    return x;
}

每合并两颗线段树，时间复杂度为两线段树上的重叠部分。

合并所有线段树，复杂度就是 $O(m \log n)$ 。

例题 : 雨天的尾巴

$\huge{线段树分裂}$

将一颗权值线段树分裂成两颗的操作，被称为线段树分裂。

一般指原有线段树的下表为 $[1, n]$ ，然后将 $[s, t]$ 的一段取出，得到两颗线段树。

先看代码：

void split(int &p, int &q, int s, int t, int l, int r) {
    if (t < l || r < s) return;
    if (!p) return;
    if (l <= s && t <= r) {
        q = p; p = 0;
        return;
    }
    if (!q) q = ++ tot;
    int mid = s + t >> 1;
    if (l <= mid) split(tr[p].l, tr[q].l, s, mid, l, r);
    if (r > mid) split(tr[p].r, tr[q].r, mid + 1, t, l, r);
    pushup(p), pushup(q);
}

类似线段树合并，时间复杂度仍然是两线段树上的重叠部分，总时间复杂度 $O(m \log n)$ 。

例题 : 线段树分裂