树状数组仅支持单点修改+区间查询或者区间修改+单点查询。
前缀和
给定一个长度为$n(n ≤ 10^5 )$的序列 $𝑎$。
有很多次询问，每次询问一个区间和：
$Q \ l \ r$ 询问 $𝑎_{[𝑙\, , 𝑟]}$ 的区间和
动态前缀和
给定一个长度为 $n(n ≤ 10^5 )$ 的序列𝑎(初值全为0)。
有很多次操作，每个操作可能是：
$Q \ l \ r$ 询问$𝑎_{[𝑙\, , \,𝑟]}$ 的区间和
$M \ x \ y$ 将 $𝑎_x$ 的值改为 $𝑎_x + y$
如使用朴素的前缀和算法，每一次修改操作后需要重新扫一遍数组。
能否找出一个能够尽可能地重复利用信息的方法呢？
树状数组
每一个整数都可以表示成 $2$ 的幂次的和的形式，
那么一个序列是否也可以表示成一系列子序列的和呢？
令 $c_{i}=a_{i-2}{ }^{k}+1+a_{i-2}{ }^{k}+2+\cdots+a_{i}$
其中 $k$ 表示 $i$ 的二进制形式中末尾 0 的个数
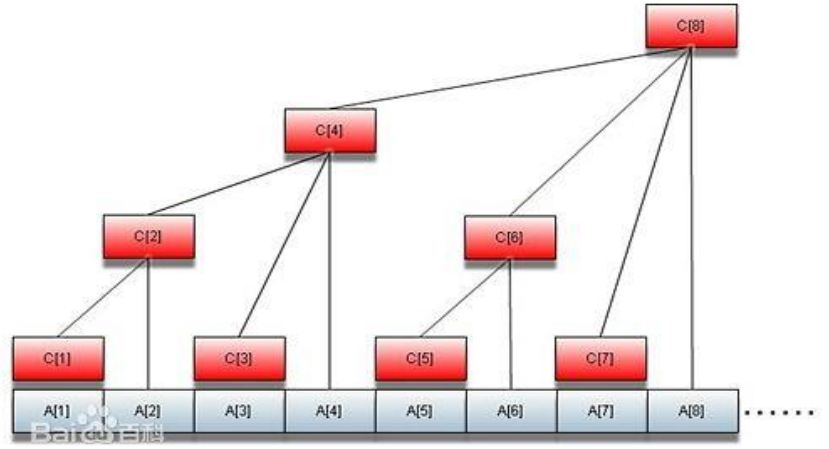
于是 $s_{i}=a_{1}+a_{2}+\cdots+a_{i}=c_{i}+a_{1}+a_{2}+\cdots+a_{i-2^{k}}=c_{i}+s_{i-2^{k}}$
$s_{i - 2^k}$又可以递归地表示下去。
由于$i$表示成二进制只有 $\log \, i$ 位，所以 $s_i$ 能表示
$c$序列中不超过 $\log \, i$ 项的和。
$a_i$ 的改变会影响到 $c_i$ 中的哪些项呢？
例：包含 $a_{11010(2)}$ 的有 $c_{11010(2)}$，$c_{11100(2)}$，$c_{100000(2)}$，$c_{1000000(2)}$
被波及到的不超过 $\log n$ 项.
设函数 $lowbit(x)$ 表示 $x$ 的二进制最低位
例：$28=00011100(2)$，lowbit $(28)=00000100(2)=4$。
lowbit $(x)=x \&(\sim x+1)=x \&-x$
查询：
$s_{i}=a_{1}+a_{2}+\cdots+a_{i}$
$=c_{i}+c_{i-\mathrm{lowbit}(i)}+c_{i- \mathrm{lowbit}(i)-\operatorname{lowbit}(i-\operatorname{lowbit}(i))}+\cdots$
int query(int x) {
int s = 0;
for (int i = x; i; i -= i & -i)
s += c[i];
return s;
}
修改：
void modify(int x, int y) {
for (int i = x; i <= n; i += i & -i)
c[i] += y;
}
单次修改和查询操作时间复杂度均为 $O(\log n)$
注意：要求元素下标必须从 1 开始，否则会出现死循环。
区间加法单点求值
给定一个长度为 $n(n \leq 10^5 )$ 的序列 $𝑎$ (初值全为0)。
有很多次操作，每个操作可能是：
- $M \ l \ r \ k$ 将 $𝑎_{[𝑙,𝑟]}$ 每个值加上 $k$
- $Q \ x $ 询问 $a_x$的值
Sol:
设差分序列 $b$，其中 $b[i]=a[i]-a[i-1]$
于是序列 $a$ 在区间 $[l,r]$ 上的区间加法，就可以转化为序列 $b$ 在 $l-1$ 和
$r$ 两个位置上的单点修改。序列 $a$ 的单点求值就可以转化为序列 $b$ 上的
前缀和。
用树状数组维护序列b的单点修改和求前缀和即可。
树状数组的作用
- 单点修改复杂度 $O(\log n)$
- 计算区间和复杂度 $O(\log n$
- 树状数组适合单个元素经常修改，而且还反复要求部分的区间的和的情况
例题：
题目： 模板】树状数组 1
Code:
#include <iostream>
#include <vector>
#include <cassert>
using namespace std;
using uint = unsigned int;
using ll = long long;
using ull = unsigned long long;
constexpr ll TEN(int n) { return (n == 0) ? 1 : 10 * TEN(n - 1); }
template <class T> using V = vector<T>;
template <class T> using W = V<V<T>>;
template <class T> struct Fenwick {
int n;
V<T> seg;
Fenwick(int _n = 0) : n(_n), seg(n + 1) {}
// 在第i个元素上+x
void add(int i, T x) {
while (i <= n) {
seg[i] += x;
i += i & -i;
}
}
// [1,i]的sum
T sum(int i) {
T s = 0;
while (i > 0) {
s += seg[i];
i -= i & -i;
}
return s;
}
// [a, b]的sum
T sum(int a, int b) { return sum(b) - sum(a); }
};
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int n, q;
cin >> n >> q;
Fenwick<ll> fw(n);
for (int i = 1; i <= n; ++i) {
ll a;
cin >> a;
fw.add(i, a);
}
for (int i = 0; i < q; ++i) {
int t;
cin >> t;
if (t == 1) {
int p;
ll x;
cin >> p >> x;
fw.add(p, x);
}
else {
ll l, r;
cin >> l >> r;
cout << fw.sum(l - 1, r) << '\n';
}
}
return 0;
}
题目： 【模板】树状数组 2
利用差分把区间查询变成单点修改，把单点查询变成区间查询
Code:
#include <iostream>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll n, m;
ll c[N];
void add(ll x, ll y) {
while (x <= n) {
c[x] += y;
x += x & -x;
}
}
ll sum(ll x) {
ll s = 0;
while (x > 0) {
s += c[x];
x -= x & -x;
}
return s;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
ll pre = 0;
for (int i = 1; i <= n; ++i) {
int x;
cin >> x;
add(i, x - pre);
pre = x;
}
for (int i = 1; i <= m; ++i) {
int t;
cin >> t;
if (t == 1) {
ll x, y, k;
cin >> x >> y >> k;
add(x, k);
add(y + 1, -k);
}
else {
ll x;
cin >> x;
cout << sum(x) << '\n';
}
}
return 0;
}
二维前缀和
给定一个矩阵 $𝑎$ (初值全为0)。有很多次询问，每个询问形如：
- $Q \ u \ d \ l \ r$ 询问 $a_{[𝑢,𝑑] ×[𝑙,𝑟]}$ 的区间和
- $M \ x \ y \ z$ 将 $𝑎_{x,𝑦}$ 的值改为 $𝑎_{x,𝑦}+z$
其实，树状数组可以简单地扩展到二维，例如修改函数只需要改成
如下形式。可惜的是，二维树状数组的空间消耗较大，在算法竞赛
中不太常用。
void modify(int x, int y, int z) {
for (int i = x; i <= n; i += i & -i)
for (int j = y; j <= m; j += j & -j)
c[i][j] += z;
}
如果矩阵过大或者稀疏矩阵的话，用树套树或者动态开点的线段树来维护更好。
逆序对
给定一个序列 $𝑎$，称满足 $1 ≤ 𝑗 < 𝑘 ≤ n$, $a_i > 𝑎_j$ 的数对 $(𝑗,𝑘)$ 为序列 $𝑎$ 的
逆序对。
定理：每次交换相邻的两个元素，序列中逆序对个数增加或减少1.
逆序对个数为冒泡排序过程中交换两个元素的次数。
求逆序对个数：归并排序或树状数组。
用树状数组求逆序对，只需要从后向前枚举数列中的数a[i]，查询
树状数组中小于a[i]的元素个数，再在树状数组让a[i]的计数增加1。
long long ans = 0;
for (int i = n; i >= 1; --i)
ans += query(a[i] - 1), modify(a[i]);
离散化
如果想要使用树状数组求逆序对，那么空间消耗与元素的最大取值是
同级别的。当元素取值范围太大时，空间消耗便会无法承受。其实，
我们只需要知道元素之间的大小关系即可，所以可以将元素的具体值
转化为值的排名，从而将空间消耗优化为与元素个数相同。
将取值转化为排名的方法叫做离散化。
离散化有多种实现方式，时间复杂度与排序的时间复杂度相同。
通过 $vector$ 对序列 $a$ 进行离散化：
vector<int> v;
for (int i = 1; i <= n; ++i)
v.push_back(a[i]);
sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
for (int i = 1; i <= n; ++i)
a[i] = lower_bound(v.begin(), v.end(), a[i]) - v.begin() + 1;
