整数二分

有序可以二分 但是可以二分的不一定有序

板子

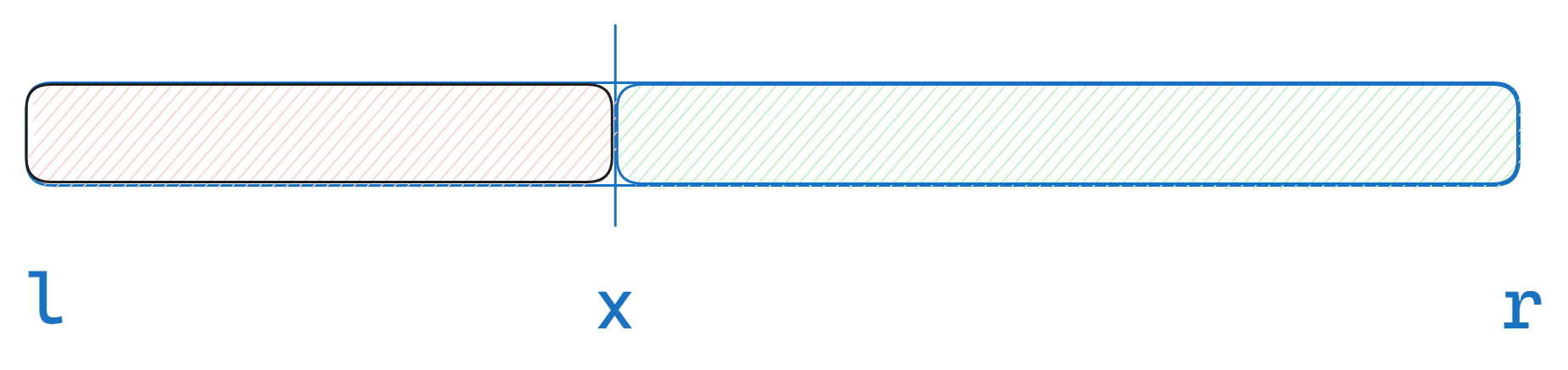
二分就是把一块区间分成左右两边 一半满足条件 一半不满足

板子一

满足条件的区间在右边的时候

r的调整

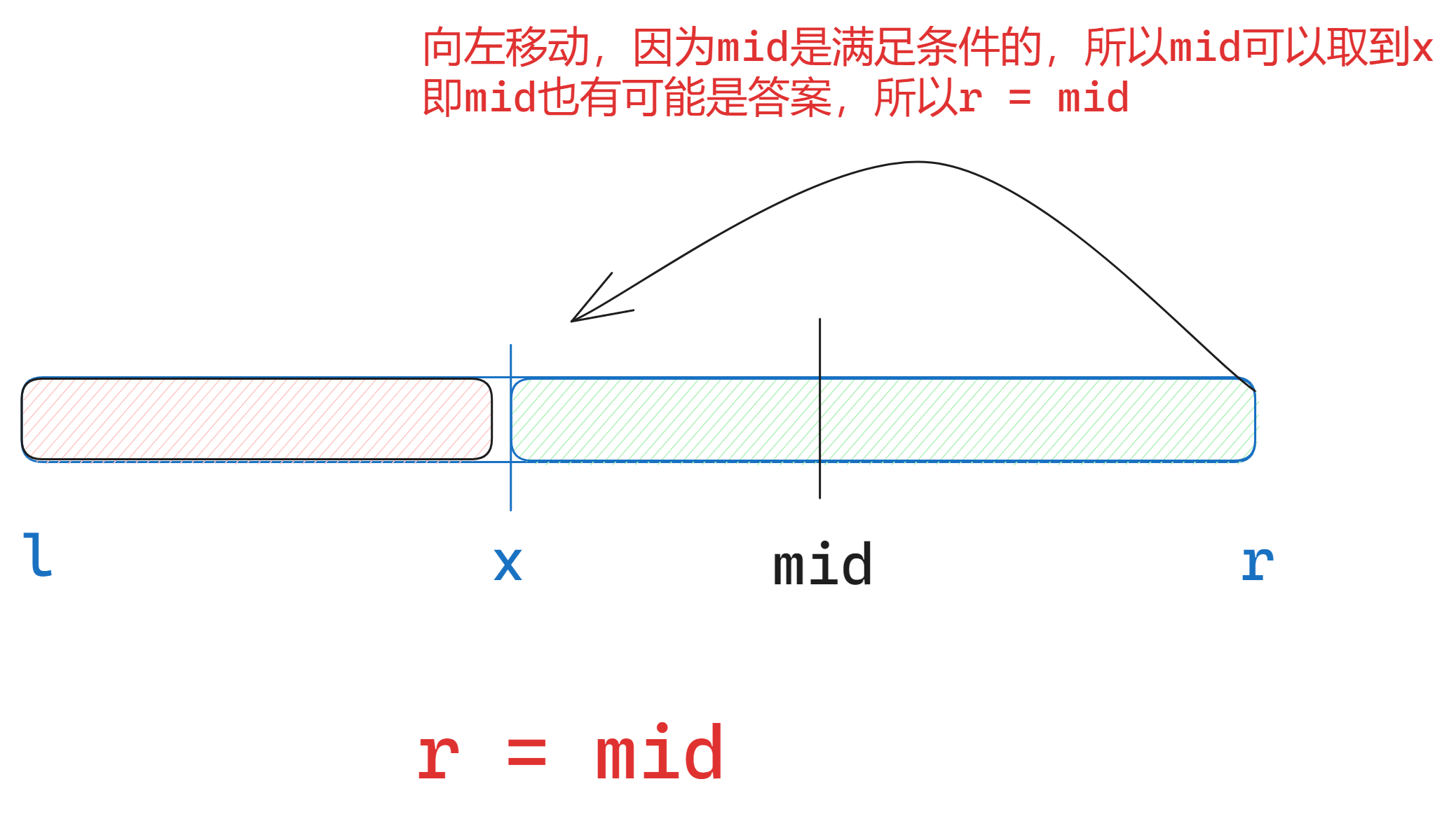
l的调整

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;    // check()判断mid是否满足性质
        else l = mid + 1;
    }
    return l;
}

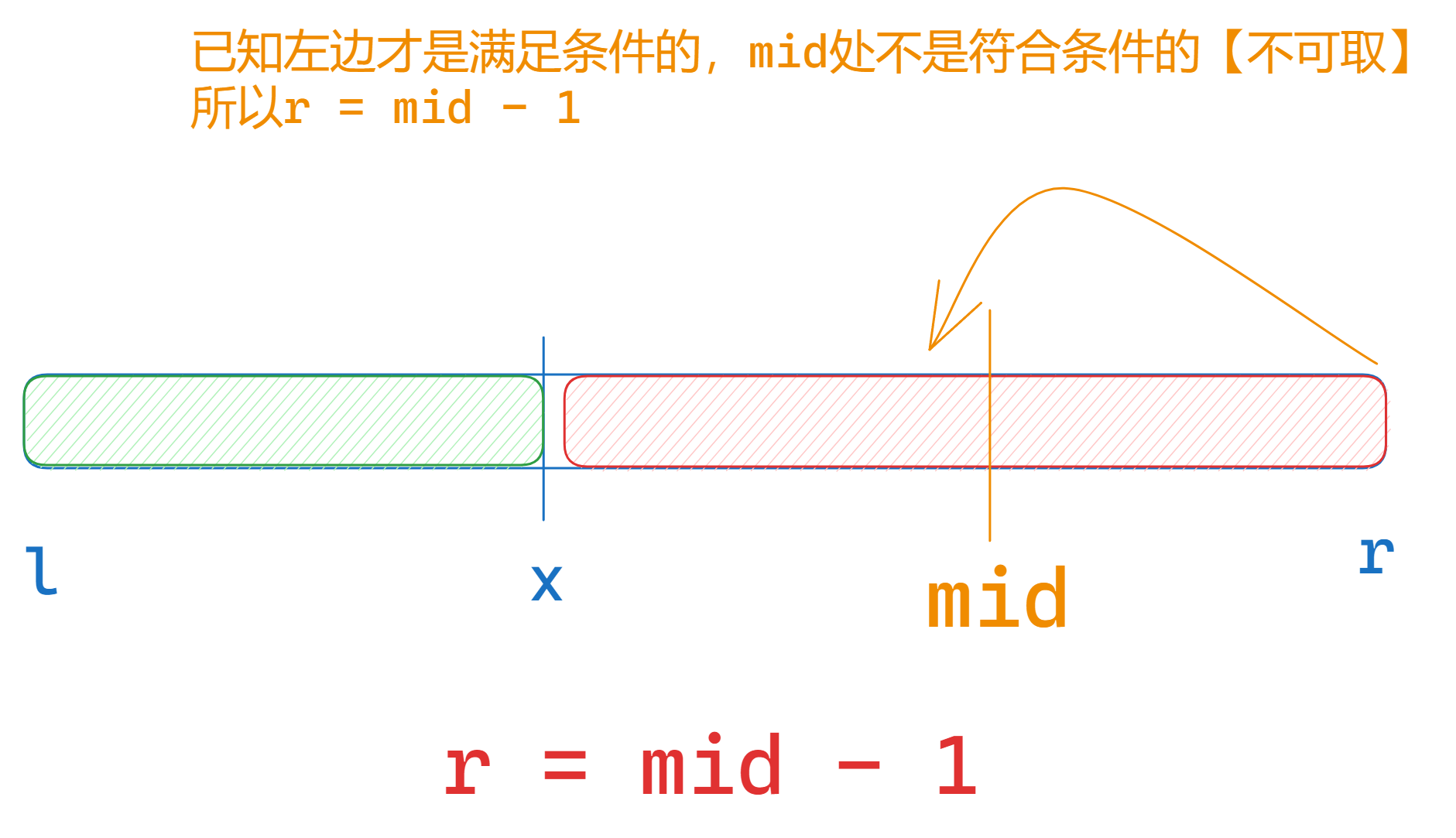
板子二

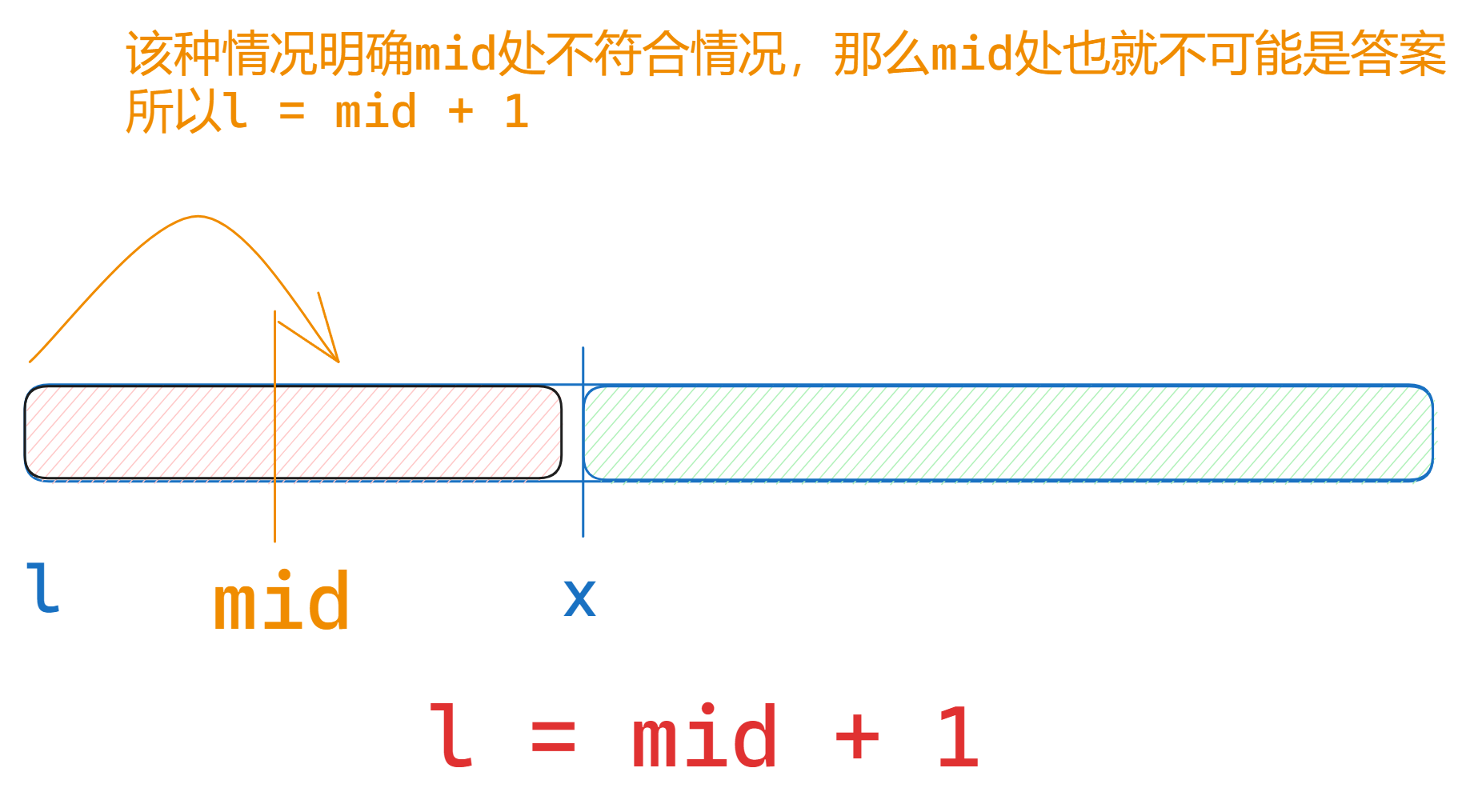
满足区间的条件在左边的时候

l的调整

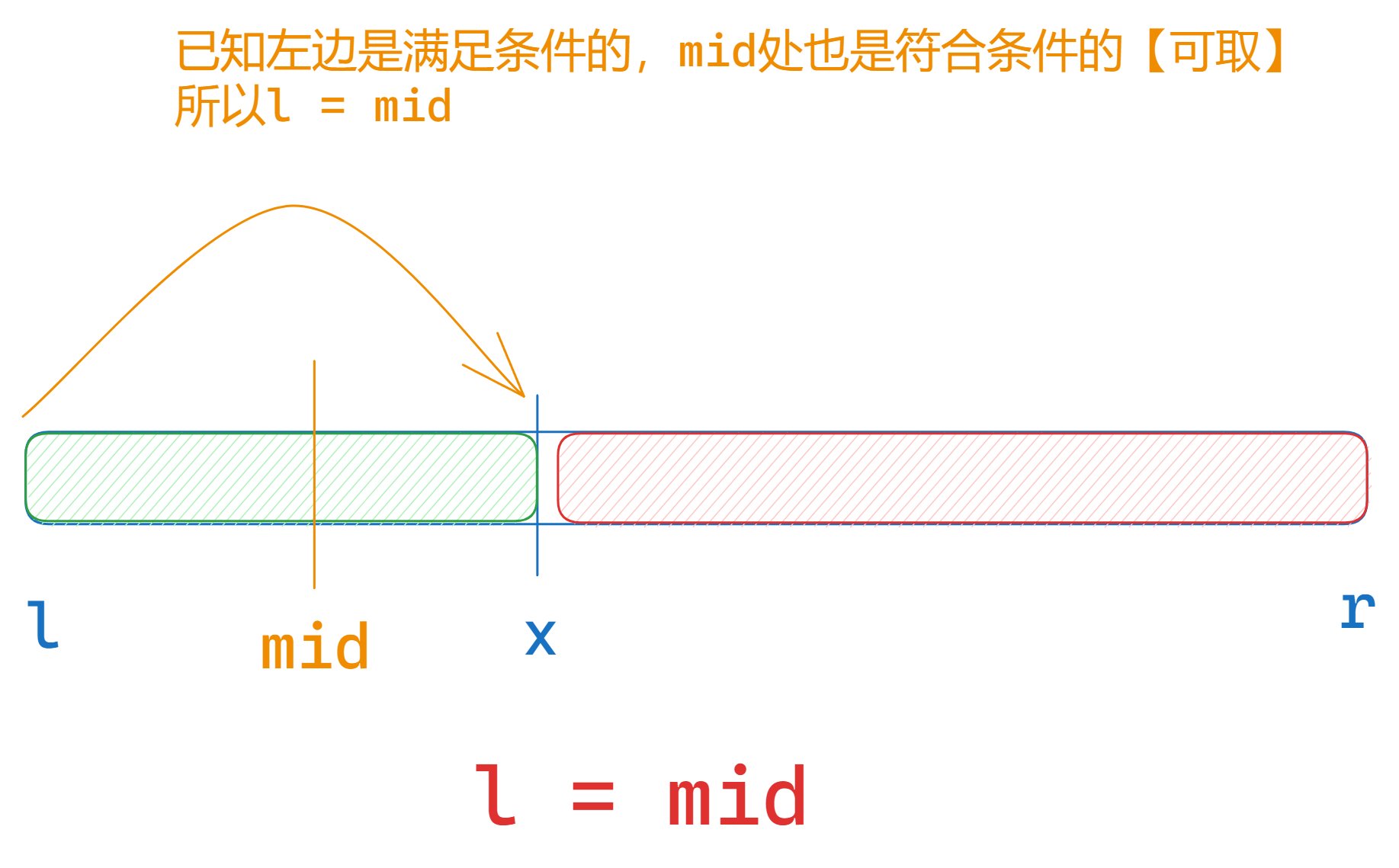
r的调整

但是！！！！

当只有两个元素的时候，如果满足左边的条件，那就要做l = mid 但是mid = l + r >> 1是下取整，会取到l，这样的话 l = mid = l，更新了一遍发现没变化，因此会陷入死循环。因此需要在计算mid的时候+1，即mid = l + r + 1 >> 1，那么当满足条件的时候 l = mid = r，因此 [r, r]两指针相遇，就会退出循环。

bool check(int x) {/* ... */} // 检查x是否满足某种性质
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{
    while (l < r)
    {
        int mid = l + r + 1 >> 1;
        if (check(mid)) l = mid;
        else r = mid - 1;
    }
    return l;
}

总结

满足条件的区间在右边用第一个板子，反之第二个板子【mid 要 + 1】