哈希，一种玄学好用的算法（她它是一种算法，哈希表才是数据结构）。

一、什么是哈希

众所周知（其实我并不知），在算法竞赛中时常会有需要用奇奇怪怪的数据类型做下标的题目（例如一些权值线段树题），但是非常显然，数组肯定是不能用什么$string、double…$甚至$vector$来做下标。那咋办，换道题？
这肯定是不能换的，那咋做？

思想历程（其实很多题除了哈希还有别的做法，并且有些题用别的方法明显更不容易错）

同学1：我会离散化！！！这题切了！！

我：很不幸，这题强制在线。。

同学1：。。。

离散化可以很快做出离线版本，但是题目是在线就不能做了。

同学2：考虑STL，使用map即可爆切此题。

我：map的常数考虑一下~~

同学2：好吧。。

map常数很大，就算底层实现是红黑树。

分享个经验：尽量不用map，十分容易超时，有一次打比赛就有一题因为map而TLE了。。

那么现在，我们还是考虑离散化的思路，但是要动态将一个数放到指定的范围中。
我们构造一个函数叫做$f$，那么我们要将$x$放到第$f(x)$个位置上。

我们一般把$f(x)$称为$hash(x)$，这就是哈希函数。

那么$hash(x)$需要满足什么条件呢？有两点：
$$1、通过x可以很快的计算hash(x) \\\ 2、\forall x \neq y,hash(x) \neq hash(y) \\\ （还有在信息学竞赛中不太常用的第三点：从hash(x)很难推出x）$$
可是非常不幸，一般的哈希函数基本都无法完全做到第二点，也就是会存在哈希冲突，也就是不能在数组中直接将第$hash(x)$个数赋值为$x$。
有什么办法吗？当然有，请看下面。

哈希表

先看一道模板题：AcWing 840.模拟散列表
通过观察我们可以发现，$x$的范围很大，但$N$的范围很小，所以可以试图把x映射成[0,N-1]区间内的数，那么可以通过取模来映射（对$N$取模）。
显然会存在两个数取模后相等，那如何解决呢？？？

1.拉链法

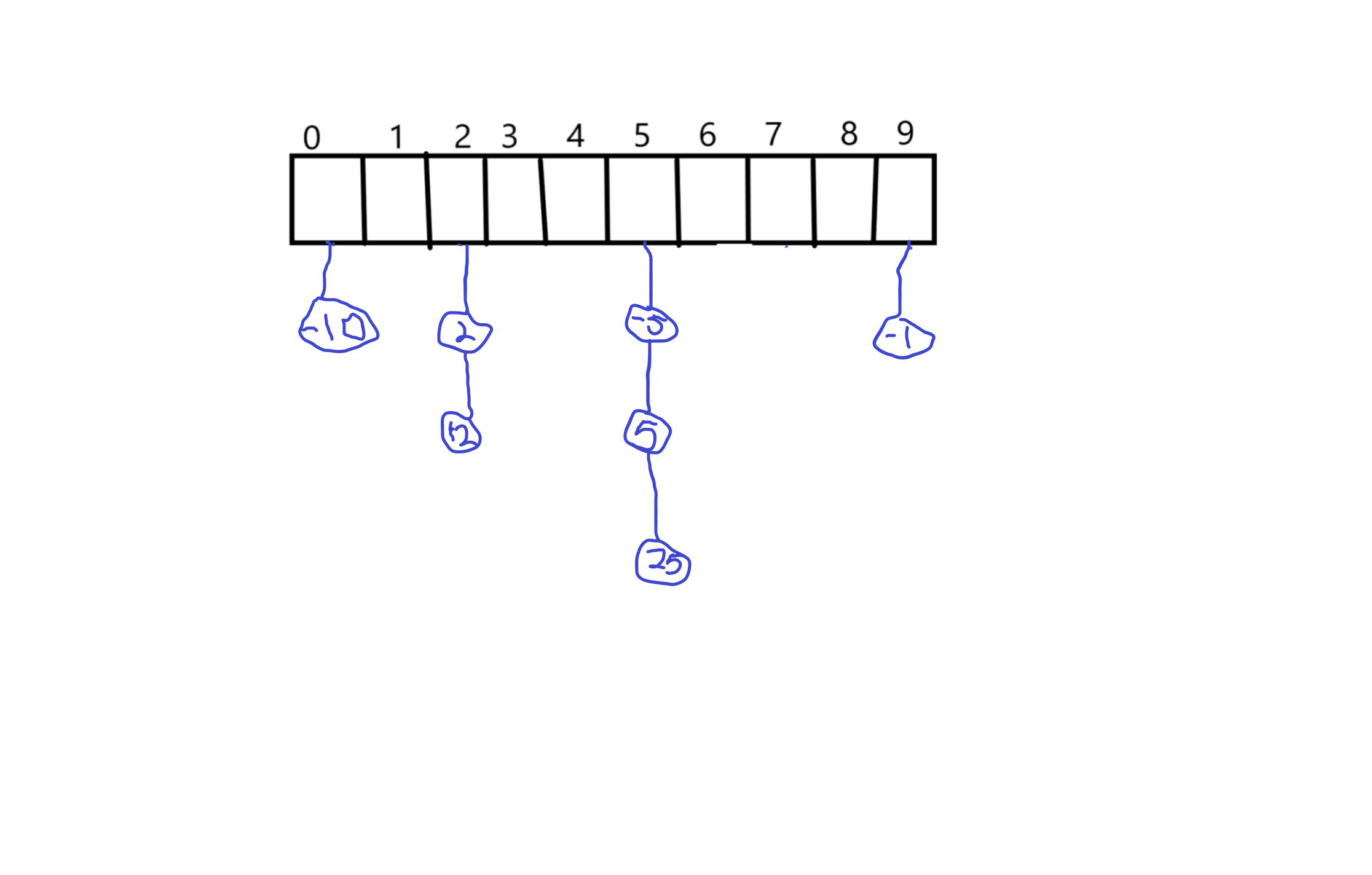
如图所示，拉链法就是开$N$个链表，若有哈希冲突，将新的那个插到链表头即可。

Code:

#include<bits/stdc++.h>
using namespace std;
int h[100003],e[100003],ne[100003],idx;
void insert(int x)
{
    int k=(x%100003+100003)%100003;
    e[idx]=x,ne[idx]=h[k],h[k]=idx++;
}
bool query(int x)
{
    int k=(x%100003+100003)%100003;
    for(int i=h[k];i!=-1;i=ne[i])
        if(e[i]==x)return 1;

    return 0;
}
int main()
{
    memset(h,-1,sizeof h);
    int n;
    cin>>n;
    while(n--){
        int x;
        char ch;
        cin>>ch>>x;
        if(ch=='I')insert(x);
        else{
            bool t=query(x);
            if(t)cout<<"Yes\n";else cout<<"No\n";
        }
    }
}

2.开放寻址法

如图所示，开放寻址法就是先找到取模的位置，如果位置有数并且这个数不是他自己就往后找，一直找到一个合适的。简单理解就像去公厕，要一直找到一个没有人的才可以进去。求这个位置的函数叫$find$函数。数组建议开到2~3倍。
Code:

#include<bits/stdc++.h>
using namespace std;
int h[300001];
int find(int x)
{
    int t=(x%300001+300001)%300001;
    while(h[t]!=0x3f3f3f3f&&h[t]!=x){
        t++;
        if(t==300001)t=0;
    }
    return t;
}
int main()
{
    memset(h,0x3f,sizeof h);
    int n;
    cin>>n;
    while(n--){
        char ch;
        int x;
        cin>>ch>>x;
        if(ch=='I')h[find(x)]=x;
        else
        {
            if(h[find(x)]==0x3f3f3f3f)cout<<"No"<<endl;else cout<<"Yes"<<endl;
        }
    }
}

附加：哈希函数的选取

实际上哈希函数大多数都可以通过取模来构造，但是有些卡常的题或者需要哈希的类型不是整数，那么取模就无能为力了，介绍以下几种方法：
$$1.取整法：将哈希函数设为hash(x)=[M \times \lbrace x \times a \rbrace]（[]表示取整，\lbrace \rbrace 表示取小数部分，a为(0,1)的常数，M为一个比较大的常数）\\\ 2.转进制法：将x看为一个P进制的数，再转为10进制 \\\ 3.各种奇奇怪怪的哈希函数：越奇怪越好，但注意再不取模之前的数一定要大于模数$$

例题：

AcWing.4185 门票
这题显然可以直接递推数列$a$，但是我们要实现快速加入一个数和快速查找一个数，所以可以用哈希表。
我们可以使用开放选址法，哈希函数也可以写成取模的：

Code:

#include<bits/stdc++.h>
#define x first
#define y second
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
typedef pair<int,int> PII;
const int M=998244353;
int n,m,k;
int h[6000010];
int find1(int x)//取模法
{
    int t=(x%6000007+6000007)%6000007;
    while(h[t]!=0x3f3f3f3f&&h[t]!=x){
        t++;
        if(t==6000010)t=0;
    }
    return t;
}
int find2(int x)//乱写1
{
    int t=(((LL)x*n%6000007-k%m)%6000007+6000007)%6000007;
    while(h[t]!=0x3f3f3f3f&&h[t]!=x){
        t++;
        if(t==6000010)t=0;
    }
    return t;
}
int find3(int x)//乱写2
{
    int t=((LL)x*(int)(sqrt(abs(x))+M)%6000007+6000007)%6000007;
    while(h[t]!=0x3f3f3f3f&&h[t]!=x){
        t++;
        if(t==6000010)t=0;
    }
    return t;
}
int find4(int x)//改进版的取整法
{
    int t=((LL)x*M%6000007+6000007)%6000007;
    while(h[t]!=0x3f3f3f3f&&h[t]!=x){
        t++;
        if(t==6000010)t=0;
    }
    return t;
}
int main()
{
    int i=0;
    cin>>n>>m>>k;
    memset(h,0x3f,sizeof h);
    int a=1;
    h[find1(a)]=a;
    while(i<2000000){
        i++;
        a=((LL)a*n+a%m)%k;
        if(h[find1(a)]==a){//可以将find1自行替换尝试
            cout<<i;
            return 0;
        }
        h[find1(a)]=a;
    }
    cout<<-1;
}