T1
题目描述
牛牛现在有一个包含$n$个正整数的数组$a$,牛牛可以将其中的每个数$a[i]$都拆成若干个和为$a[i]$的正整数,牛牛想知道拆后(也可以一个数都不拆)这个数组最多能有多少个素数。
输入描述
第一行一个正整数n代表数组长度
第二行n个正整数代表a[i]的值
$1 \leq n \leq 1e^6, 1 \leq a[i] \leq 1e^9$
输出描述
拆后数组最多的素数个数
示例1
输入
3
1 1 1
输出
0
说明
由于1不能再拆,并且1不是素数,所以拆后最多有0个素数
示例2
输入
3
5 3 7
输出
6
说明
3不拆;5可以拆成{2, 3},变成2个素数;7可以拆成{2, 2, 3},变成3个素数,所以最后拆后数组最多有6个素数
算法
(贪心) $O(n)$
- 尽量拆成$2$和$3$的组合
- 对于奇数$2x + 1$来说,可以被拆成$x - 1$个$2$和$1$个$3$,共$x$个数;对于偶数$2x$来说可拆成$x$个2,共$x$个数
- 答案有可能爆$int$
时间复杂度
扫一遍数组的时间复杂度为$O(n)$
C++ 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
int n;
int main() {
cin >> n;
long long ret = 0;
for (int i = 0; i < n; i ++ ) {
int x; cin >> x;
ret += x / 2;
}
cout << ret;
return 0;
}
T2
题目描述
现在有$n$个人排队买票,已知是早上8点开始卖票,这$n$个人买票有两种方式:
第一种是每一个人都可以单独去买自己的票,第i个人花费$a[i]$秒。
第二种是每一个人都可以选择和自己后面的人一起买票,第$i$个人和第$i + 1$个人一共花费$b[i]$秒。
最后一个人只能和前面的人一起买票或单独买票。
由于卖票的地方想早些关门,所以他想知道他最早几点可以关门,请输出一个时间格式形如:$08:00:40 am/pm$
输入描述
第一行输入一个整数$T$,接下来有$T$组测试数据。
对于每一组测试数据:输入一个数$n$,代表有$n$个人买票。
接下来$n$个数,代表每一个人单独买票的时间$a[i]$
接下来$n - 1$个数,代表每一个人和她前面那个人一起买票需要的时间$b[i]$
$1 \leq T \leq 100$
$1 \leq n \leq 2000$
$1 \leq a[i], b[i] \leq 50$
输出描述
对于每组数据,输出一个时间,代表关门的时间
示例1
输入
2
2
20 25
40
1
8
输出
08:00:40 am
08:00:08 am
算法
(动态规划) $O(T \times n)$
- $f[i]$表示前$i$个人买票需要的最短时间
- 初始时,第一个人只能自己买
- 从第二个人开始,要么自己买,要么跟前面一个人一起买
- 状态转移方程:$f[i] = min(f[i - 1] + a[i], f[i - 2] + b[i - 1])$
- 从8点开始卖票,时间要再加个8
时间复杂度
$T$组数据,每组$DP$时间复杂度为$O(n)$
C++ 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 2010;
int T, n;
int a[N], b[N], f[N];
int main() {
cin >> T;
while (T -- ) {
cin >> n;
for (int i = 1; i <= n; i ++ ) cin >> a[i];
for (int i = 1; i <= n - 1; i ++ ) cin >> b[i];
f[1] = a[1];
for (int i = 2; i <= n; i ++ )
f[i] = min(f[i - 1] + a[i], f[i - 2] + b[i - 1]);
int &t = f[n];
int h = t / 3600 + 8, m = t % 3600 / 60, s = t % 60;
bool status = true;
if (h > 12) h -= 12, status = false;
printf("%02d:%02d:%02d %s\n", h, m, s, status ? "am" : "pm");
}
return 0;
}
T3
题目描述
现在有$n$个物品,每一个物品都有一个价值,现在想将这些物品分给两个人,要求这两个人每一个人分到的物品的价值总和相同(个数可以不同,总价值相同即可),剩下的物品就需要扔掉,现在想知道最少需要扔多少价值的物品才能满足要求分给两个人。
输入描述
第一行输入一个整数$T$,代表有T组测试数据。
对于每一组测试数据,一行输入一个整数$n$,代表物品的个数。
接下来$n$个数,$a[i]$代表每一个物品的价值。
$1 \leq T \leq 10$
$1 \leq n \leq 15$
$1 \leq a[i] \leq 100000$
输出描述
对于每一组测试数据,输出一个答案代表最少需要扔的价值。
示例1
输入
1
5
30 60 5 15 30
输出
20
说明
样例解释,扔掉第三个和第四个物品,然后将第一个物品和第五个物品给第一个人,第二个物品给第二个人,每一个人分到的价值为60,扔掉的价值为20。
算法
(回溯) $O(T \times 3 ^ n)$
- $a、b、c$分别表示第一个人获得的价值、第二个人获得的价值、扔掉的价值
- 答案的上界为全部物品价值之和
- 枚举当前物品给第一个人还是给第二个人还是扔掉
- 最高的广告牌
时间复杂度
每层3个分支,$n$层$O(3 ^ n)$
C++ 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 20;
int T, n, ret;
int w[N];
int a, b, c;
void dfs(int u) {
if (u == n) {
if (a == b) ret = min(ret, c);
return;
}
a += w[u];
dfs(u + 1);
a -= w[u];
b += w[u];
dfs(u + 1);
b -= w[u];
c += w[u];
dfs(u + 1);
c -= w[u];
}
int main() {
cin >> T;
while (T -- ) {
cin >> n;
ret = 0;
for (int i = 0; i < n; i ++ ) cin >> w[i], ret += w[i];
dfs(0);
cout << ret << endl;
}
return 0;
}
T4
题目描述
在一次聚会中,教授们被要求写下自己认可哪位教授的学术成果(也可以写自己,且可能出现重复)。已知,如果教授$A$认可教授$B$,且教授$B$认可教授$C$,那么即可视为教授$A$也认可教授$C$。现在我们想知道有多少队教授是两两互相认可的?
输入描述
第一行两个正整数,教授人数$n$,以及认可关系总数$m$;
接下来$m$行,每行两个正整数$x$和$y$,表示教授$x$认可教授$y$($x、y$可能相等且可能出现重复)
$n \leq 50000$
$m \leq 600000$
输出描述
一行一个数字表示答案,即互相认可的教授有多少对。
示例1
输入
5 6
1 3
2 1
3 2
3 5
4 5
5 4
输出
4
说明
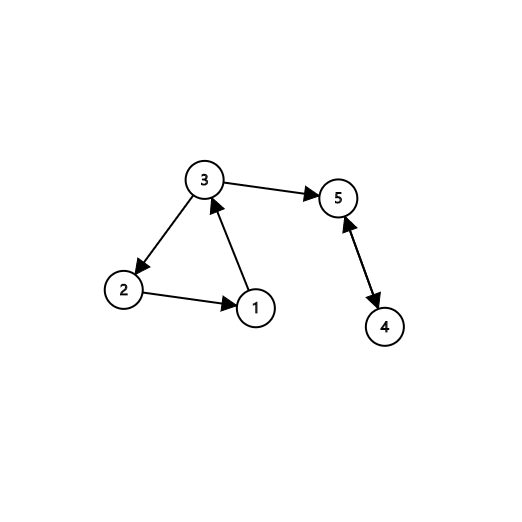
4对互相认可的教授分别是1和2、1和3、2和3、4和5。
算法
(有向图的强连通分量) $O(n + m)$
- 如果教授$A$认可教授$B$,则存在有向边$A \rightarrow B$
- 用$targan$算法求一遍有向图强连通分量即可
- 最后的答案是$\sum_{i = 1}^{scc-cnt}C_{cnt[i]}^2$
- 这题有10%的样例没过,不知道为啥(可能是最后计算答案时需要转成long long)
时间复杂度
每个顶点都被访问了一次,且只进出了一次栈,每条边也只被访问了一次,所以该算法的时间复杂度为$O(n + m)$
C++ 代码
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 5e4 + 10, M = 6e5 + 10;
int n, m;
int h[N], e[M], ne[M], idx;
int stk[N], top;
bool in_stk[N];
int dfn[N], low[N], timestamp;
int cnt[N], scc_cnt;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
void targan(int u) {
dfn[u] = low[u] = ++ timestamp;
stk[ ++ top] = u, in_stk[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
if (!dfn[j]) {
targan(j);
low[u] = min(low[u], low[j]);
} else if (in_stk[j]) {
low[u] = min(low[u], dfn[j]);
}
}
if (dfn[u] == low[u]) {
scc_cnt ++ ;
int y;
do {
y = stk[top -- ];
in_stk[y] = false;
cnt[scc_cnt] ++ ;
} while (y != u);
}
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
for (int i = 0; i < m; i ++ ) {
int a, b; cin >> a >> b;
add(a, b);
}
for (int i = 1; i <= n; i ++ )
if (!dfn[i])
targan(i);
long long ret = 0;
// 之前没写long long
for (int i = 1; i <= scc_cnt; i ++ ) ret += (long long)cnt[i] * (cnt[i] - 1) / 2;
cout << ret;
return 0;
}


### tql
Orz%%%%%%%%
%%%%
TQL