前言
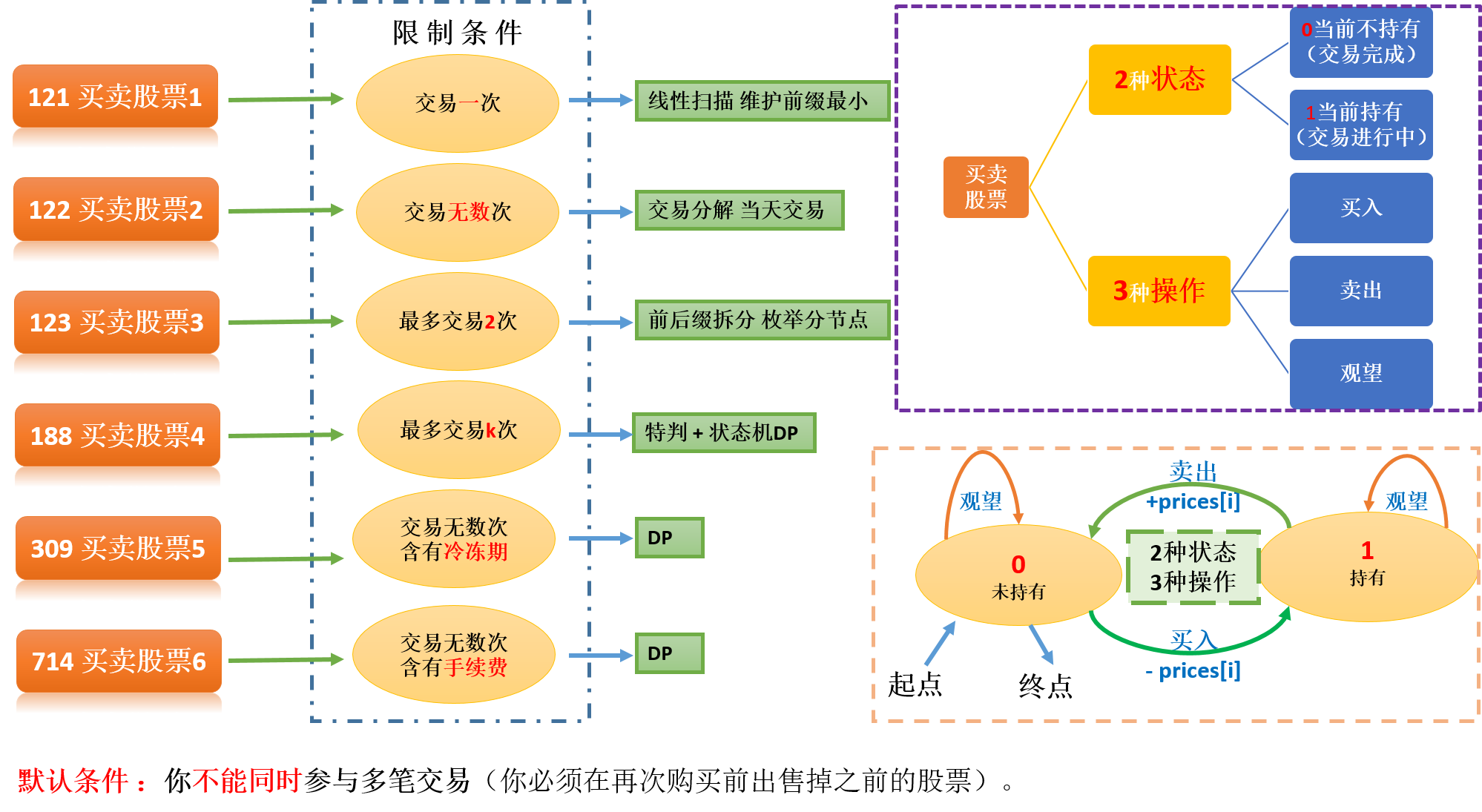
leetcode上关于股票买卖的最佳时机有6道题目,限制条件为买卖的次数,以及买卖的冷冻期或者手续费等。
默认制约的条件为:不能同时参与多笔交易(必须在再次购买前出售掉之前的股票)
股票买卖问题概述
两种状态
- 持有 | 正在交易
- 不持有 | 交易完成
三种动作
- 买入
- 卖出
- 什么也不做(观望)
附加条件
- 买卖次数
- 1次
- 2次
- K次
- 无数次(最大到
n/2,n为天数)- 冷冻期
- 手续费
默认条件
你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
买卖一次算一笔交易
121 买卖股票的最佳时机
思路
从前到后扫描,枚举卖出天,减去之前最小的买入价格
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
// 从前到后枚举再哪一天卖出,找到之前的最小值
// 第i天卖出,维护找到0 ~ i- 1 中的最小值
for(int i = 0, minp = INT_MAX; i < prices.size(); i++)
{
res= max(res, prices[i] - minp);
min_p = min(minp, prices[i]);
}
return res;
}
};
122 买卖股票的最佳时机 ii
思路
可以买卖多次,只要
有收益就进行操作。核心:把交易分解为
若干天单天的的交易,把收益为正的加起来;
class Solution {
public:
int maxProfit(vector<int>& prices) {
int res = 0;
for(int i = 1; i < prices.size() ; i++)
res += max(0, prices[i] - prices[i-1]);
return res;
}
};
相似题目 :1163. 纪念品
123 买卖股票的最佳时机 iii
思路
常见技巧 :前后缀分解, 枚举
分界点
- 两个独立的子问题 : 前缀的最大值 后缀的最大值
若枚举第二次交易买入的时间,假设为
i。
则前i天的最大收益 :f(i) = max(f(i -1), prices[i] - minp)
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
vector<int> f(n + 2); // 下标从1开始 便于计算
for(int i = 1, minp = INT_MAX; i <= n; i ++) //枚举哪天卖出
{
f[i] = max(f[i - 1], prices[i - 1] - minp);
minp = min(minp, prices[i- 1]);
}
int res = 0;
for(int i = n, maxp = 0; i >= 1; i --) // 枚举后半段哪天买入[i ~ n -1] , 则前面为 [0 ~ i -1]
{
res = max(res, maxp - prices[i - 1] + f[i - 1]);
maxp = max(maxp, prices[i - 1]);
}
return res;
}
};
相似题目 : 构建乘积数组 最大的和
188 买卖股票的最佳时机 IV
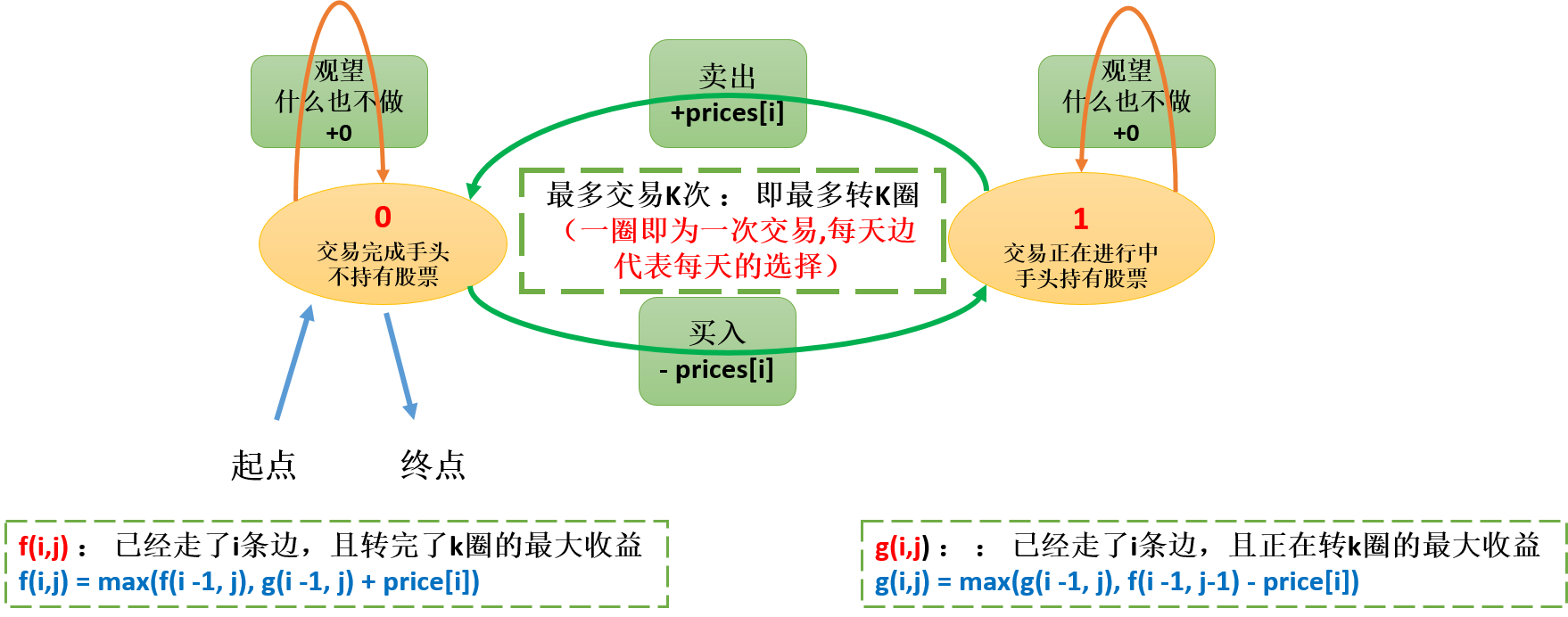
思路 :状态机模型dp
交易的阶段
- 0 交易完 手头不持有
- 1 还未交易, 手头持有
结合图有
f(i,j) = max(f(i - 1, j), g(i - 1, j) + price[i])
g(i,j) = max(g(i - 1, j), f(i - 1, j - 1) - price[i])
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
const int INF = 1e8;
int n = prices.size();
if(k >= n/2) // 最多交易 n/2 相当于交易无限次 分解交易
{
int res = 0;
for(int i = 1; i < n; i++)
res += max(0, prices[i] - prices[i -1]);
return res;
}
// 交易k次 状态机模型dp
vector<vector<int>> f(n + 1, vector<int>(k + 1, -INF));
auto g = f;
int res = 0;
f[0][0] = 0;
for (int i = 1; i <= n; i ++ ) // 下标从1开始 注意偏移量
for (int j = 0; j <= k; j ++ ) { // 这里从1开始, 注意边界问题
f[i][j] = max(f[i - 1][j], g[i - 1][j] + prices[i - 1]);
g[i][j] = g[i - 1][j];
if (j) g[i][j] = max(g[i][j], f[i - 1][j - 1] - prices[i - 1]);
// 只有j >= 1才能和第二项取max
res = max(res, f[i][j]);
}
return res;
}
};
无论是f(i)还是g(i),之和上一层有关旭,利用滚动数组优化空间。
&1即可 相当于%2,机械化的修改
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
const int INF = 1e8;
int n = prices.size();
if(k >= n/2) // 相当于交易无限次 分解交易
{
int res = 0;
for(int i = 1; i < n; i++)
res += max(0, prices[i] - prices[i -1]);
return res;
}
// 交易k次 状态机模型dp
vector<vector<int>> f(2, vector<int>(k + 1, -INF));
auto g = f;
int res = 0;
f[0][0] = 0; // 状态初始化 只有一个入口
for (int i = 1; i <= n; i ++ ) // 下标从1开始, 注意偏移量
for (int j = 0; j <= k; j ++ )
{
f[i & 1][j] = max(f[i - 1 & 1][j], g[i - 1 & 1][j] + prices[i - 1]);
g[i & 1][j] = g[i - 1 & 1][j];
if (j) g[i & 1][j] = max(g[i & 1][j], f[i - 1 & 1][j - 1] - prices[i - 1]);
res = max(res, f[i & 1][j]);
}
return res;
}
};
309. 最佳买卖股票时机含冷冻期
思路
每天都会有三种选择,买入(受到冷冻期的限制)、卖出、什么都不做。
f(i): 第i天结束后,当天不持有股票的最大收益。【不持有一定不能买入,则有两种选择】
- 1) 当天卖出,则不持有。能卖出说明前一天即
i-1必定持有,即f(i) = g(i-1) + prices[i]- 2) 当天什么都不做,说明前一天
i-1也不持有 ,即f(i) = f(i-1)
g(i): 第i天结束后,当天持有股票的最大收益。【持有则一定不能卖出,则有两种选择】。
- 1) 当天买入,则持有。因为有一天冷冻期,前天结束时即
i-2天不持有股票才能买,即g(i)= f(i-2) - prices[i]- 2) 当天什么也不做,前一天持有,则当天一定持有,即
g(i) = g(i-1)综上
f(i) = max(f(i -1), g(i-1) + prices[i])
g(i) = max(g(i -1), f(i-2) - prices[i])
class Solution {
public:
int maxProfit(vector<int>& prices) {
int n = prices.size();
if(!n) return 0;
// 状态的表示
vector<int> f(n); // 第i天结束后,当天不持有股票的最大收益
vector<int> g(n); // 第i天结束后,当天持有股票的最大收益
// 根据定义赋初值
f[0] = 0, g[0] = - prices[0];
// 状态的计算
for(int i = 1; i < n; i++)
{
f[i] = max(f[i - 1], g[i - 1] + prices[i]); // 卖掉就是正收益,说明前一天必持有
if(i >= 2)
g[i] = max(g[i - 1], f[i - 2] - prices[i]); // 买入就是负收益
else
g[i] = max(g[i - 1], - prices[i]);
}
return f[n - 1];
}
};
714.最佳买卖股票时机含手续费
思路
每天都会有三种选择,买入、卖出、什么都不做
1)手续费在卖出的时候收取
f(i): 第i天结束后,当天不持有股票的最大收益。【不持有则一定不能买入,有两种选择】
- 1) 当天卖出,则不持有。能卖出说明前一天即
i-1必定持有,记得加收手续费;
即f(i) = g(i-1) + prices[i]- fee- 2) 当天什么都不做,说明前一天
i-1也不持有 ,即f(i) = f(i-1)
g(i): 第i天结束后,当天持有股票的最大收益。【持有则一定不能卖出,有两种选择】。
- 1) 当天买入,则持有。能买,说明前一天结束时,也就是
i-1天不持有股票才能买。
即g(i)= f(i-1) - prices[i]- 2) 当天什么也不做,前一天持有,则当天一定持有,即
g(i) = g(i-1)综上
f(i) = max(f(i -1), g(i-1) + prices[i] - fee)
g(i) = max(g(i -1), f(i-1) - prices[i])注意: 之和上一层有关系,可以利用
滚动数据进行空间优化
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
if(!n) return 0;
// 状态的表示
vector<int> f(n); // 第i天结束后,当天不持有股票的最大收益
vector<int> g(n); // 第i天结束后,当天持有股票的最大收益
// 根据定义赋初值 假设买入的时候付手续费
f[0] = 0 ;
g[0] = -prices[0] ;
// 状态的计算
for(int i = 1; i < n; i++)
{
f[i] = max(f[i - 1], g[i - 1] + prices[i] - fee); // 卖掉就是正收益,说明前一天必持
g[i] = max(g[i - 1], f[i - 1] - prices[i]) ; // 买入就是负收益
}
return f[n-1];
}
};
---------------------------------------------------------------------------------------------------
// 利用滚动数组优化
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
if(!n) return 0;
int a = 0;
int b = -prices[0] ;
for(int i = 1; i < n; i++)
{
int tmp = a;
a = max(a, b + prices[i] - fee);
b = max(b, tmp - prices[i]) ;
}
return a;
}
};
2)若手续费在买入的时候收取
f(i) = max(f(i -1), g(i-1) + prices[i])
g(i) = max(g(i -1),f(i-1) - prices[i] - fee)
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
if(!n) return 0;
// 状态的表示
vector<int> f(n); // 第i天结束后,当天不持有股票的最大收益
vector<int> g(n); // 第i天结束后,当天持有股票的最大收益
// 根据定义赋初值 假设买入的时候付手续费
f[0] = 0 ;
g[0] = -prices[0] - fee ;
// 状态的计算
for(int i = 1; i < n; i++)
{
//int tmp = f[i - 1];
f[i] = max(f[i - 1], g[i - 1] + prices[i] ); // 卖掉就是正收益,说明前一天必持
g[i] = max(g[i - 1], f[i - 1] - prices[i] - fee) ; // 买入就是负收益
}
return f[n-1];
}
};
---------------------------------------------------------------------------------------------------
// 空间优化
class Solution {
public:
int maxProfit(vector<int>& prices, int fee) {
int n = prices.size();
if(!n) return 0;
int a = 0;
int b = -prices[0] - fee ;
for(int i = 1; i < n; i++)
{
int tmp = a;
a = max(a, b + prices[i]);
b = max(b, tmp - prices[i] - fee) ;
}
return a;
}
};
总结
- 前后缀分解的思想
- 状态机dp的空间优化
- 交易分解的思想拓展

