二，广度优先搜索

在深度优先搜索中，我们知道它是一种采用一路搜到底搜索策略，感觉就是一种很执着的算法，而这次的广度优先搜索则是一层一层的搜索，所以我们需要多维护一个队列，通常情况下，队列刚开始只有一个起始状态，然后取出这个状态，扩展它能达到的所有状态，往队列后面插，然后重复这个操作，直到队列为空，直观的感觉就是一杯水倒在地上，水在地上快速的扩展边界。相对于深度优先搜索来说，广度优先搜索除了可以求连通性，由于是一层一层往外扩展且边权为一，还可以求最小步数。缺点是如果某层搜索空间过大，有溢出的风险。BFS 的重点在于队列，而 DFS 的重点在于递归。这是它们的本质区别。

下面是BFS算法在图上的遍历顺序

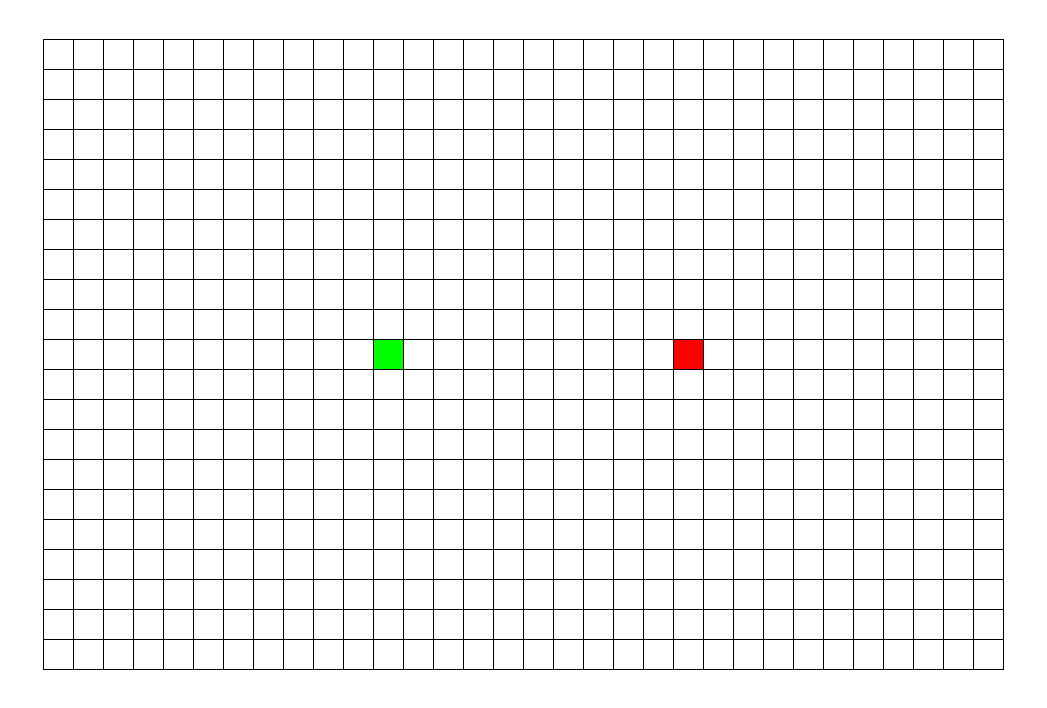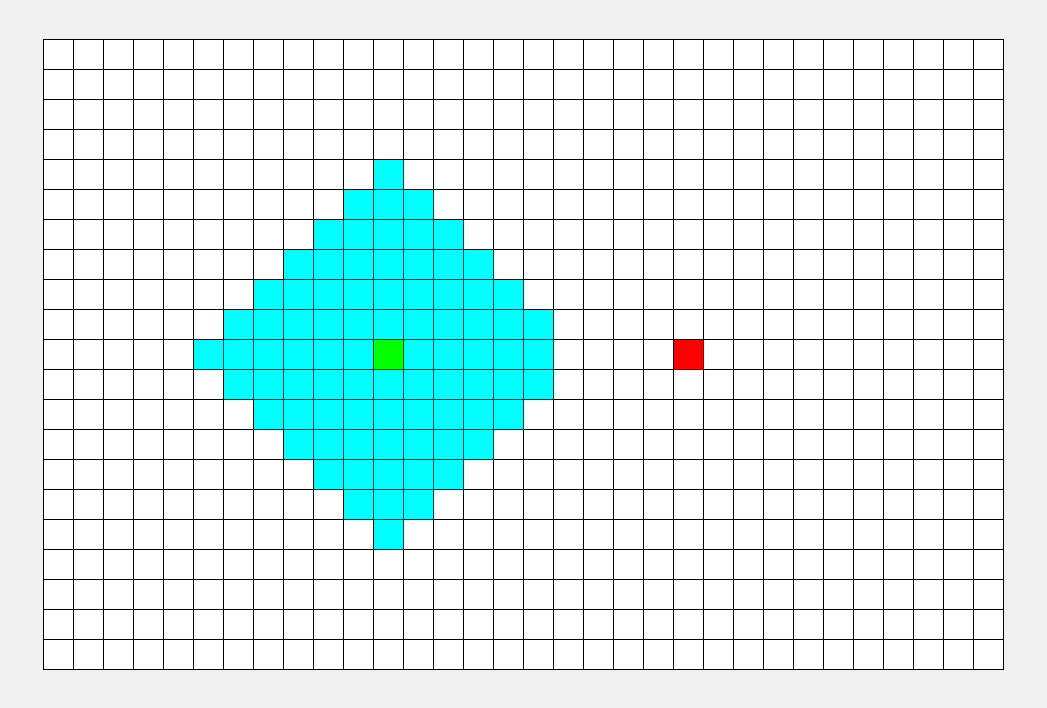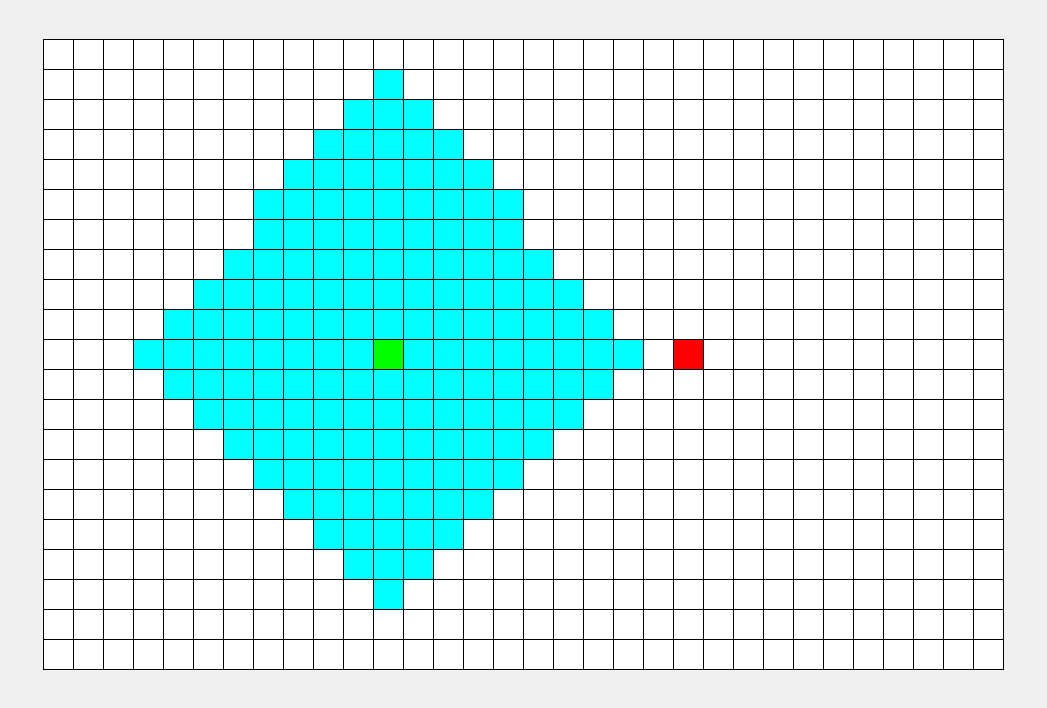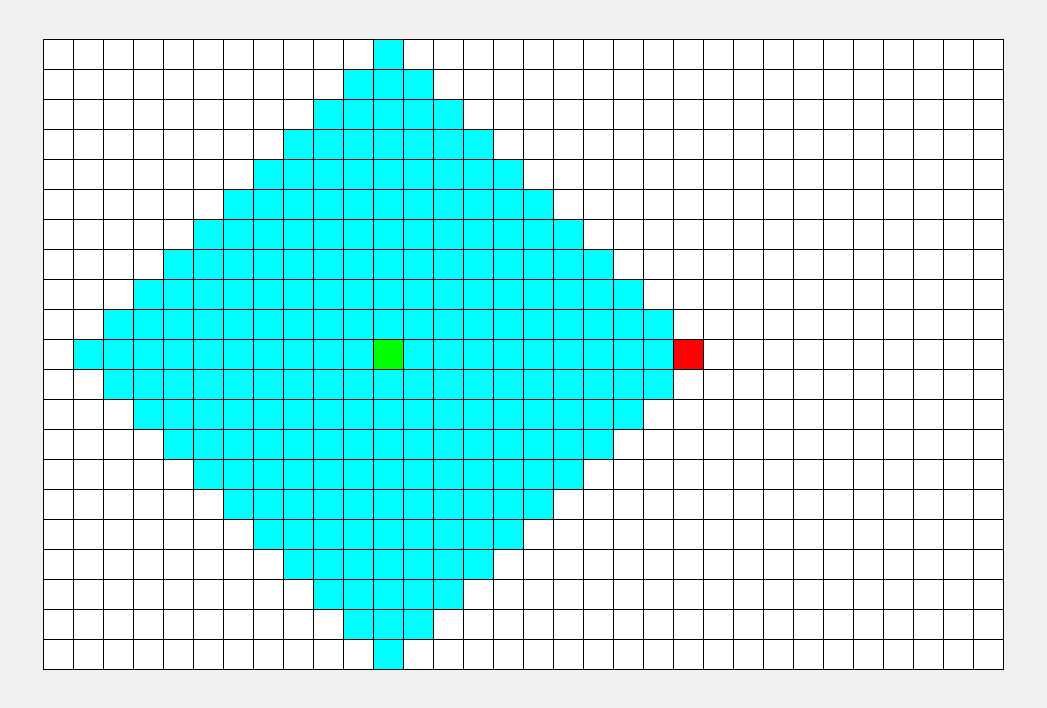
举个典型例子，如下图，灰色代表墙壁，绿色代表起点，红色代表终点，规定每次只能走一步，且只能往下或右走。求一条绿色到红色的最短路径。

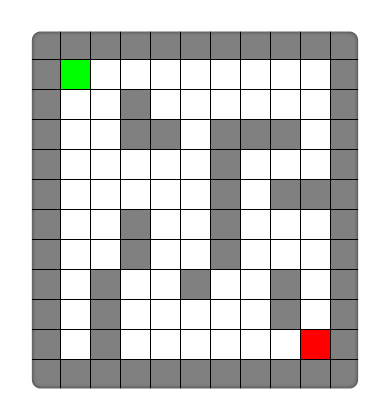
( 图片来源地址 )

虽然DFS 和 BFS 算法都可以做，但是DFS算法还有加个额外判断，判断起点到终点所有路径中的最短路径，而BFS算法是一层一层扩展的，每次扩展到就是最短距离，时间复杂度O（N），所以针对该问题，BFS可以处理的更优秀。

例题
题目地址： 立体推箱子
题目大意：见题目。。。

• 解析::本题难点在于状态表示，
• 箱子共有三种状态：
  立着，记录为 0
  竖躺着，记录为 1
  横躺着，记录为 2
  每个状态又有不同的变化规律，可以尝试自己体验这个游戏来找到规律，这里就不在叙述了 游戏地址 ： 立体推箱子

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

const int N = 510;

struct State
{
    int x,y;
    int lie;
}start,en;

int n,m;
char map[N][N];
int dist[N][N][3];

bool check(int x,int y){

    return x >=0 && x < n && y >= 0 && y < m && map[x][y] != '#';
}

int bfs(State start , State end){

    queue<State> q;
    memset(dist, -1, sizeof dist);
    dist[start.x][start.y][start.lie] = 0;
    q.push(start);

    int d[3][4][3] = {
        {{-2, 0, 2}, {0, 1, 1}, {1, 0, 2}, {0, -2, 1}},
        {{-1, 0, 1}, {0, 2, 0}, {1, 0, 1}, {0, -1, 0}},
        {{-1, 0, 0}, {0, 1, 2}, {2, 0, 0}, {0, -1, 2}}
    };

    while (q.size())
    {
        auto t = q.front();
        q.pop();

        for (int i = 0; i < 4; i ++ )
        {
            State next = {t.x + d[t.lie][i][0], t.y + d[t.lie][i][1], d[t.lie][i][2]};

            int x = next.x, y = next.y;
            if (!check(x, y)) continue;
            if (next.lie == 0)
            {
                if (map[x][y] == 'E') continue;
            }
            else if (next.lie == 1)
            {
                if (!check(x, y + 1)) continue;
            }
            else
            {
                if (!check(x + 1, y)) continue;
            }

            if (dist[next.x][next.y][next.lie] == -1)
            {
                dist[next.x][next.y][next.lie] = dist[t.x][t.y][t.lie] + 1;
                q.push(next);
            }
        }
    }

    return dist[end.x][end.y][end.lie];

}
int main(){

    while(cin >> n >> m , n || m )
    {
        for(int i = 0 ; i < n ;i++)cin >> map[i];
        memset(dist,-1,sizeof(dist));
        start = {-1};
        for(int i = 0 ; i < n ; i++)
           for(int j = 0 ; j < m ; j++)
              if(map[i][j] == 'X' && start.x == -1)
              {
                  if(map[i + 1][j] == 'X')start = {i , j , 2};
                  else if(map[i][j + 1] == 'X')start = {i , j , 1};
                  else start = {i , j , 0};
              }
              else if(map[i][j] == 'O')en = {i , j, 0};

        int res = bfs(start , en );

        if(res == -1)puts("Impossible");
        else cout << res << endl;
    }   
    return 0;
}

Flood(洪水覆盖算法)

原理就是广度优先搜索的遍历顺序，从一个点扩展，直到到达该连通域边界，就像是洪水覆盖，把该片区域全部淹没，一般用来求联通块个数。

例题
题目链接: 池塘计数
题目大意：农夫约翰有一片 N∗M 的矩形土地。现在用一个字符矩阵来表示他的土地。每个单元格内，如果包含雨水，则用”W”表示，如果不含雨水，则用”.”表示。现在，约翰想知道他的土地中形成了多少片池塘。每组相连的积水单元格集合可以看作是一片池塘。每个单元格视为与其上、下、左、右、左上、右上、左下、右下八个邻近单元格相连。请你输出共有多少片池塘，即矩阵中共有多少片相连的”W”块。

• 解析：入门水题，一般实际中遇不到这么简单的题。。就是求连通块个数。

#include <iostream>
using namespace std;

typedef pair<int,int> PII;

const int N = 1010;


int n,m,res;
char g[N][N];
PII q[N * N ];
bool st[N][N];


void bfs(int x,int y){
     int hh = 0, tt = 1;
    q[0] = {x, y};
    st[x][y] = true;

    while(hh != tt)
    {
        PII t = q[hh++];

        for(int i = t.first - 1 ; i <= t.first + 1 ; i++ )
            for(int j = t.second - 1 ; j <= t.second + 1 ; j++)
            {
                if(i == t.first && j == t.second)continue;
                if(st[i][j])continue;
                if(i < 0 ||i >= n || j < 0 || j >= m)continue;
                if(g[i][j] == '.')continue;

                q[tt++] = {i,j};
                st[i][j] = true;
            }
    }

}

int main(){

     scanf("%d%d", &n, &m);
    for (int i = 0; i < n; i ++ ) scanf("%s", g[i]);

    int cnt = 0;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            if (g[i][j] == 'W' && !st[i][j])
            {
                bfs(i, j);
                cnt ++ ;
            }

    printf("%d\n", cnt);


    return 0;
}

其他例题： 城堡 ， 山峰和山谷

多源BFS

多源BFS：问题有多个起点向外扩展，可以看作是这些起点是由一个虚拟源点且连向它们的边权为一扩展而来的,而且满足单调性和二段性，普通BFS有的性质它都有。

例题
题目地址： 矩阵距离
题目大意：给定一个N行M列的01矩阵A，A[i][j] 与 A[k][l] 之间的曼哈顿距离定义为：
dist(A[i][j],A[k][l])=|i−k|+|j−l|
输出一个N行M列的整数矩阵B，其中：
B[i][j]=min1≤x≤N,1≤y≤M,A[x][y]=1dist(A[i][j],A[x][y])

• 解析：把每个一当做起点用BFS向外扩展，求出每个点距离最近的“1”的最短路，

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

typedef pair<int , int > PII;

const int N = 1e3 + 10;

int n,m;
char a[N][N];
int dist[N][N];
int dx[] = {-1 , 0 , 1 , 0} , dy[] = {0 , 1 , 0 , -1};

bool check(int x,int y){
    return x >=0 && x < n && y >= 0 && y < m && dist[x][y] == -1;
}

void bfs(){

    queue<PII> q;
    memset(dist,-1,sizeof(dist));
    for(int i = 0 ; i < n ; i++)
      for(int j = 0 ; j < m ; j++)
          if(a[i][j] == '1')
            {
                dist[i][j] = 0;
                q.push({i , j});
            }

    while(q.size())
    {
        auto t = q.front();
        q.pop();

        int x = t.first, y = t.second;
        for(int i = 0 ; i  <  4 ; i++)
        {
            int nx = x + dx[i] , ny = y + dy[i]; 
            if(check(nx,ny))
            {
                dist[nx][ny] = dist[x][y] + 1;
                q.push({nx,ny});
            }
        }
    }

}

int main(){

    cin >> n >> m;

    for(int i = 0 ; i < n ; i++)
      for(int j = 0 ; j < m ; j++)
          cin >> a[i][j];

    bfs();

    for(int i = 0 ; i < n ; i++)
       {
           for(int j = 0 ; j < m ;j++)
               cout << dist[i][j] << ' ';

            cout << endl;
       }  

    return 0;
}

广搜变形

双端队列BFS：如果边权不全为一，有1又有0，我们就需要使用双端队列BFS了，每个状态向外扩展如果边权为一放到后面，为0放前面，很容易知道该队列满足二段性和单调性，这是很重要的性质，保证每次取出一定是最短距离
优先队列BFS：队于更加普遍的情况，也就是每次扩展都有各自不同的“代价”，求出每个点到其点的最短距离，相当于在一张图上去求最短公路，对应图论的dijkstra算法，由于Dijkstra被证明是正确的，所以这个这个也是正确的。

双端队列例题
题目地址： 电路维修
题目大意：见题目。。

• 解析：把每个点当做状态，只能沿着对角线走，如果从一个点到另外一个点没用对角线相连，则边权为一否则为0
• 别人的题解： 秦淮岸

#include <cstring>
#include <iostream>
#include <algorithm>
#include <deque>

using namespace std;

typedef pair<int,int> PII;

const int N = 510;

int n,m;
char s[N][N];
int d[N][N];

int dx[] = {-1,-1,1,1},dy[] = {-1,1,1,-1};
int ix[] = {-1,-1,0,0},iy[] = {-1,0,0,-1};
char xs[] = "\\/\\/";
bool st[N][N];

int bfs(){

      memset(st, false , sizeof(st));
    memset(d,0x3f,sizeof(d));
    deque<PII> dp;
    dp.push_back({0,0});
    d[0][0] = 0;

    while(dp.size())
    {
        auto p = dp.front();
        dp.pop_front();
        int x = p.first , y = p.second;
        if(x == n && y == m )return d[x][y];
        if(st[x][y])continue;
        st[x][y] = true;


        for(int i = 0 ; i < 4 ; i++)
        {
            int a = x + dx[i] , b = y + dy[i];
            if(a >= 0 && a <= n && b >= 0 && b <= m)
            {
                int w = 0;
                int j = x + ix[i] , k = y + iy[i];
                if(s[j][k] != xs[i])w = 1;
                if(d[a][b] > d[x][y] + w)
                {
                    d[a][b] = d[x][y] + w;
                    if(w == 1)dp.push_back({a,b});
                    else dp.push_front({a,b});
                }
            }

        }
    }
  return -1;
}

int main(){
    int T;
    cin >> T;
    while(T--)
    {   
        cin >> n >> m;
        for(int i = 0 ; i < n ;i++)cin >> s[i];
        if(n % 2 != m % 2){
           cout << "NO SOLUTION"<<endl;
            continue;
        }

        int t = bfs();
        if(t == -1)cout << "NO SOLUTION"<<endl;
        else cout << t <<endl;
    }

    return 0;
}

优先队列BFS例题
题目地址： 装满油箱
题目大意：。。。。

• 解析：使用一个二元组（city，fuel）表示每个状态city –城市编号 ， fuel – 剩余汽油量，起始状态为（s ， 0）,每个状态有两个分支
• 1，若fuel < c 可以加一升汽油，扩展到新状态（city ， fuel + 1），花费为该城市加一升汽油的价钱
• 2，若当前状态的汽油量足以去往下一个城市next ， 那么扩展新状态（next ， fuel - w） w 为 去往该城市消耗的汽油量，即边权

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1010, C = 110, M = 20010;

int n, m;
int h[N], e[M], w[M], ne[M], idx;
int price[N];
int dist[N][C];
bool st[N][C];

struct Ver
{
    int d, u, c;
    bool operator< (const Ver &W)const
    {
        return d > W.d;
    }
};

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra(int start, int end, int cap)
{
    memset(dist, 0x3f, sizeof dist);
    memset(st, false, sizeof st);
    priority_queue<Ver> heap;
    heap.push({0, start, 0});
    dist[start][0] = 0;

    while (heap.size())
    {
        auto t = heap.top(); heap.pop();

        if (t.u == end) return t.d;

        if (st[t.u][t.c]) continue;
        st[t.u][t.c] = true;

        if (t.c < cap)
        {
            if (dist[t.u][t.c + 1] > t.d + price[t.u])
            {
                dist[t.u][t.c + 1] = t.d + price[t.u];
                heap.push({dist[t.u][t.c + 1], t.u, t.c + 1});
            }
        }

        for (int i = h[t.u]; ~i; i = ne[i])
        {
            int j = e[i];
            if (t.c >= w[i])
            {
                if (dist[j][t.c - w[i]] > t.d)
                {
                    dist[j][t.c - w[i]] = t.d;
                    heap.push({dist[j][t.c - w[i]], j, t.c - w[i]});
                }
            }
        }
    }

    return -1;
}

int main()
{
    scanf("%d%d", &n, &m);
    memset(h, -1, sizeof h);
    for (int i = 0; i < n; i ++ ) scanf("%d", &price[i]);
    for (int i = 0; i < m; i ++ )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c), add(b, a, c);
    }

    int query;
    scanf("%d", &query);
    while (query -- )
    {
        int a, b, c;
        scanf("%d%d%d", &c, &a, &b);
        int t = dijkstra(a, b, c);
        if (t == -1) puts("impossible");
        else printf("%d\n", t);
    }

    return 0;
}

双向BFS

有明确的初态和终态，那么就可以从两个状态分别开始，轮流扩展各一层，当有某个状态重合时，就说明初态和终态可以相连，可以合并成初态到终态的最小步数。

如下图所示，在某一层的某个状态可以使两棵树相的根节点相连：

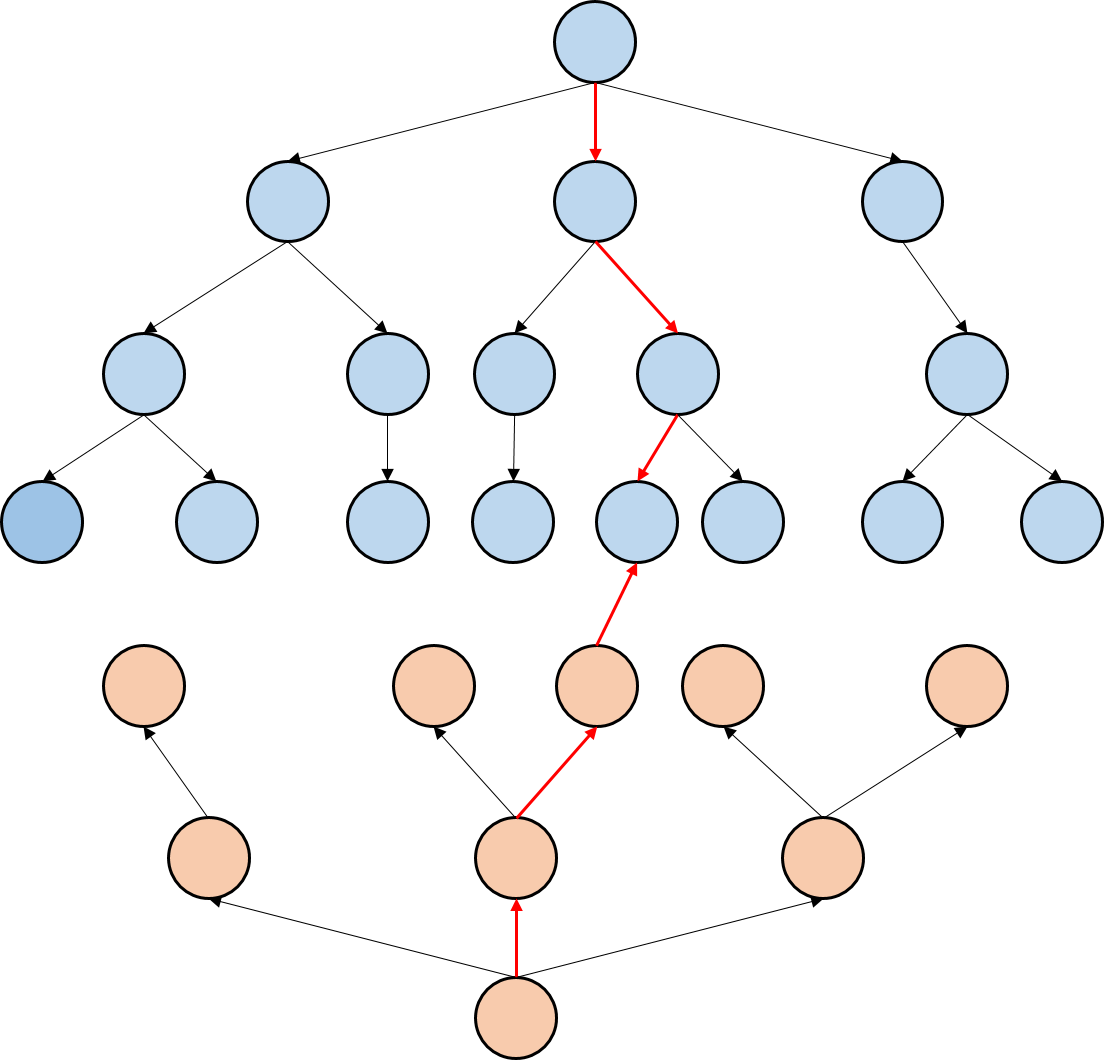
例题
题目地址： 噩梦
题目大意：。。。。

• 解析：从男孩所在位置和女孩所在位置轮流扩展，并扩展的状态是否在魔鬼的曼哈顿距离内，该时间点即为所求

#include <iostream>
#include <queue>
#include <cstring>
using namespace std;

const int N = 810;

typedef pair<int,int> PII;

int n,m,cnt;
int st[N][N];
char map[N][N];
PII girl,boy , ghost[2];
int dx[] = {-1,0,1,0} , dy[] = {0 , 1 , 0 , -1};

bool check(int a,int b,int k){
    if(a < 0 || a >= n || b < 0 || b >= m || map[a][b] == 'X' )return false;

    for(int i = 0 ; i < 2 ; i++)
       if(abs(a - ghost[i].first )+ abs(b - ghost[i].second) <= 2 * k) 
           return false;

   return true;
}

int bfs(){

    memset(st,0,sizeof(st));
    queue<PII> qb,qg;
    qb.push(boy);
    qg.push(girl);
    int step = 0;
    while(qb.size() || qg.size())
    {
       step++;        
        for(int i = 0 ; i < 3 ; i++)
           for(int j = 0 , len = qb.size() ; j < len ; j++)
           {
               auto t = qb.front();
               qb.pop();
               int x = t.first , y = t.second;
               if(!check(x,y,step))continue;
               for(int k = 0 ; k < 4 ; k++)
               {
                   int a = x + dx[k] , b = y + dy[k];
                   if(check(a,b,step))
                   {
                       if(st[a][b] == 2)return step;
                       else if(st[a][b] == 0)
                       {
                           qb.push({a,b});
                           st[a][b] = 1;
                       }
                   }
               }

           }


         for(int i = 0 ; i < 1; i++)
           for(int j = 0 , len = qg.size() ; j < len ; j++)
           {
               auto t = qg.front();
               qg.pop();
               int x = t.first , y = t.second;
               if(!check(x,y,step))continue;
               for(int k = 0 ; k < 4 ; k++)
               {
                   int a = x + dx[k] , b = y + dy[k];
                   if(check(a,b,step))
                   {
                       if(st[a][b] == 1)return step;
                       else if(st[a][b] == 0)
                       {
                           qg.push({a,b});
                           st[a][b] = 2;
                       }
                   }
               }

           }

    }
    return -1;

}

int main(){

   int T;
   cin >> T;

   while(T--)
   {
       cin >> n >> m;
       cnt = 0;
       for(int i = 0 ; i < n ;i++)cin >> map[i];

       for(int i = 0 ; i < n ;i++)
         for(int j = 0 ; j < m ; j++)
             if(map[i][j] == 'M')boy = {i , j};
             else if(map[i][j] == 'G')girl = {i , j};
             else if(map[i][j] == 'Z')ghost[cnt++] = {i , j};

       cout << bfs() << endl;         
   }



    return 0;
}

A_sta

在原有基础上增加一个估价函数，就变成了启发式搜索，优先搜索最有可能到达终点的状态进行扩展，避免了大量多余操作，但是在无解的情况下，会退化成普通的BFS，甚至还会多出logn的复杂度，具体去看下面几篇文章

参考阅读： 路径规划之 A* 算法 ， 百度百科-astar （启发式搜索算法） ， A*算法详解

设计估价函数需要注意的点：
估价不能大于真实值，加入该点估价大于真实值，而从该点可以扩展到最优解，但是该点由于估价值比真实值大，就可能无法取出来扩展
估价函数最好有单调性。

例题
题目地址： 第k短路
题目大意：求到终点第k短的路径

• 解析：很显然，用归纳法证明，当第一次从队列出来的终点是最短路，那么第二次就是第二短，所以第k次取出来的就是第k短。估价函数我们可以设成从终点出发到每个的点的最短距离，显然这具有单调性，反向建图即可
  

从网上找到一个关于第一次取出来的一定是最短的比较完整的证明，只看到这个英文的，懒得打了~~~

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
typedef pair<int, PII> PIII;
const int N = 1e3 + 10, M = 2e5 + 10;

int n,m,idx;
int s,t,k;
int h[N],rh[N],e[M],ne[M],w[M];
int st[N];
int d[N];

void add(int h[],int a,int b,int c){
    e[idx] = b , ne[idx] = h[a] , w[idx] = c, h[a] = idx++;
}

void dijkstra(){
    d[t] = 0;
    priority_queue<PII,vector<PII>, greater<PII>> q;
    q.push({0,t});

    while(q.size())
    {
        auto ver = q.top();
        q.pop();
        if(st[ver.second])continue;
        st[ver.second] = 1;
        for(int i = rh[ver.second] ; ~i ; i = ne[i])
        {
            int j = e[i];
            if(d[j] > d[ver.second] + w[i])
            {
               //cout <<"--------------------"<<endl;
                d[j] = d[ver.second] + w[i];
                q.push({d[j],j});             
            }
        }
    }
}

int A_star(){

    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    heap.push({d[s], {0, s}});

    memset(st, 0, sizeof st);

    while (heap.size())
    {
        auto temp = heap.top();
        heap.pop();

        int ver = temp.y.y, distance = temp.y.x;
        st[ver] ++ ;

        if (ver == t && st[ver] == k) return distance;
        if(st[ver] > k)continue;
        for (int i = h[ver]; ~i; i = ne[i])
        {
            int j = e[i];
            heap.push({distance + w[i] + d[j], {distance + w[i], j}});
        }
    }
    return -1;
}

int main(){
    memset(d,0x3f,sizeof(d));
    memset(h,-1,sizeof(h));
    memset(rh , -1 , sizeof(rh));

    scanf("%d%d", &n, &m);

    int a,b,c;
    for(int i = 0 ; i < m ; i++)
    {
        scanf("%d%d%d", &a, &b, &c);
        add(h,a,b,c),add(rh,b,a,c);
    }

   scanf("%d%d%d", &s, &t, &k);
    if(s == t)k++;
    dijkstra();
   // cout << d[1] <<endl;
    printf("%d\n", A_star());

    return 0;
}