一，深度优先搜索

顾名思义，就是一种按深度优先的顺序的搜索算法，可以将“问题状态空间”看做一棵搜索树，深度优先就是从树根一直往下搜，遇到不可解就回溯，往其它方向继续向下扩展，像子集和和全排列问题，还有N皇后问题都可以深度优先搜索算法解决，它是一种暴力解决NP问题的非常直观的方法。

它在图上的搜索顺序大概如下图所示
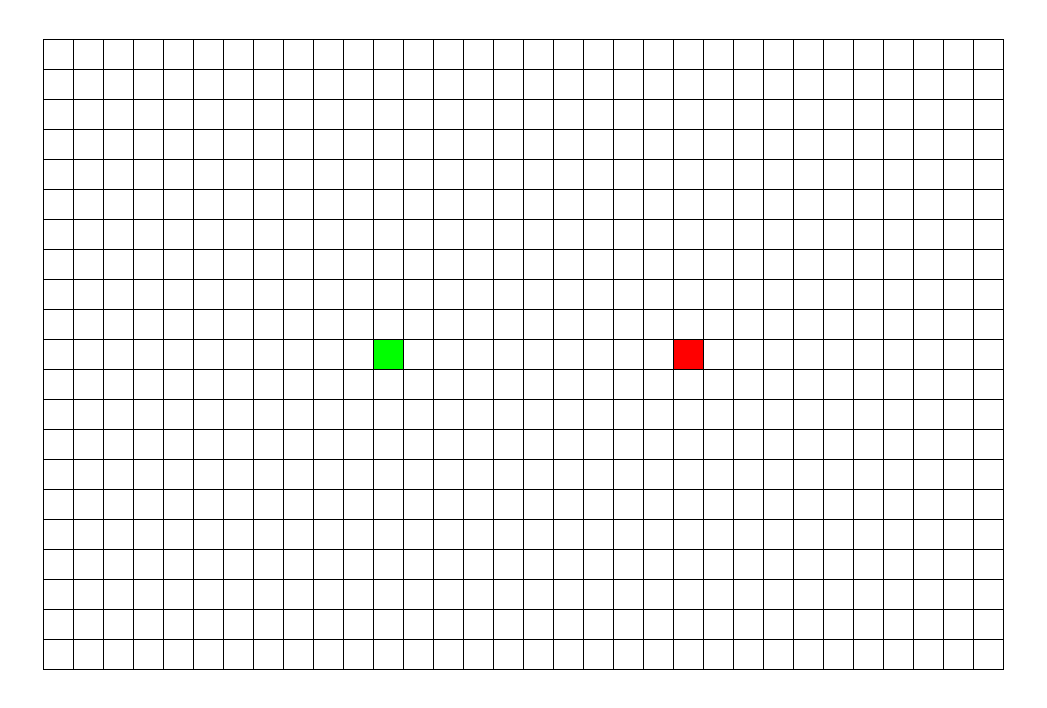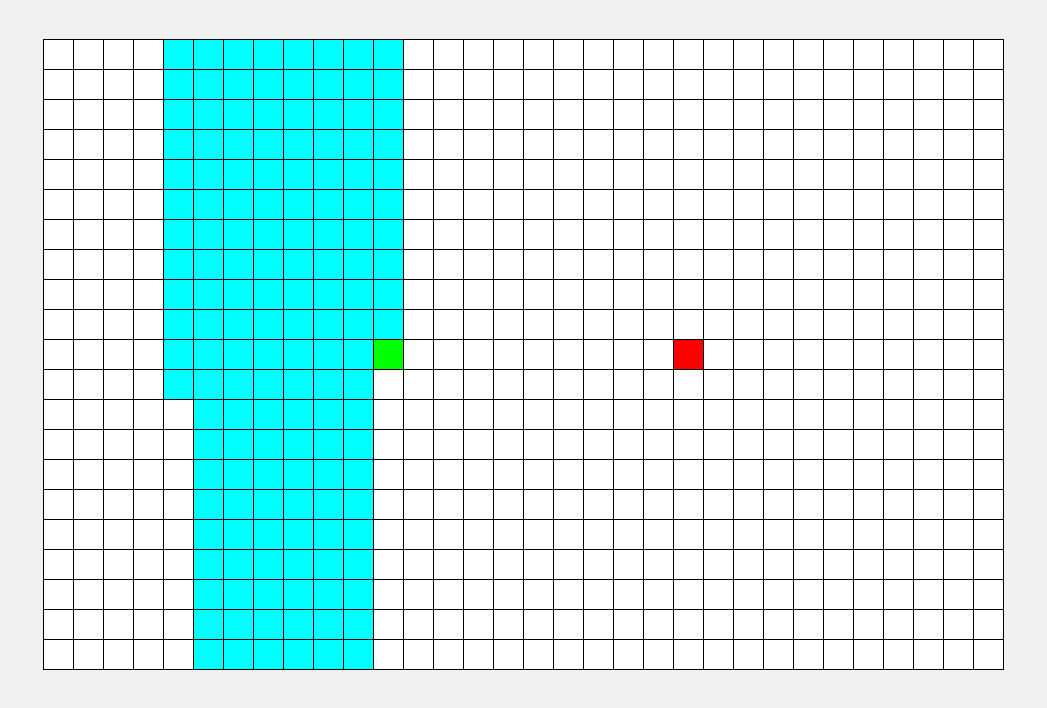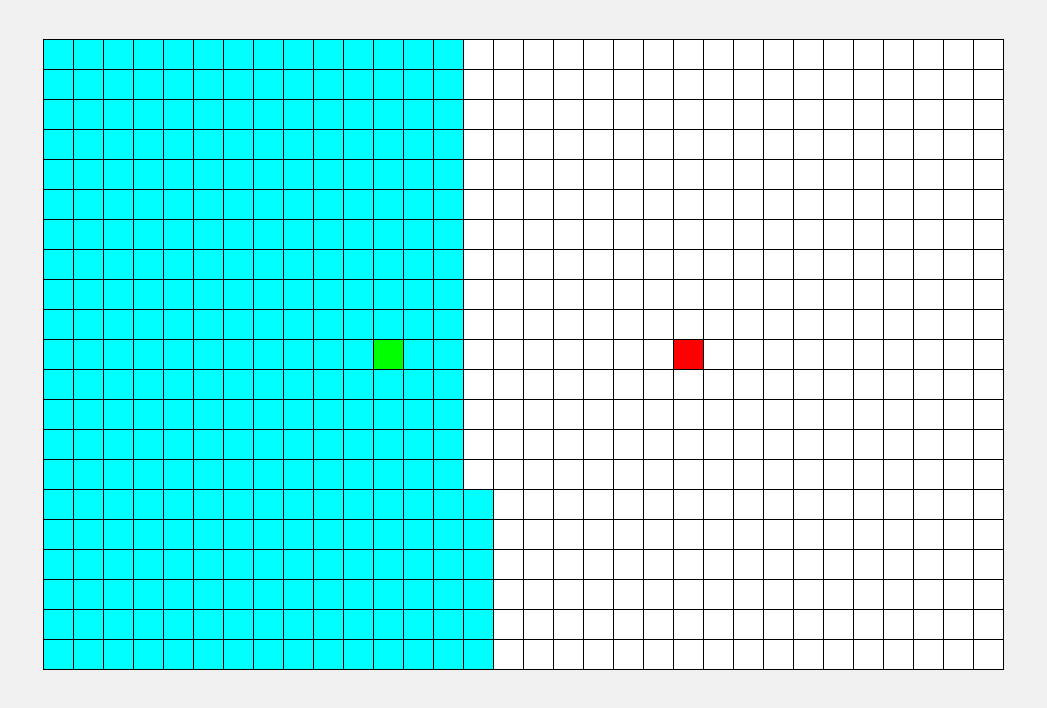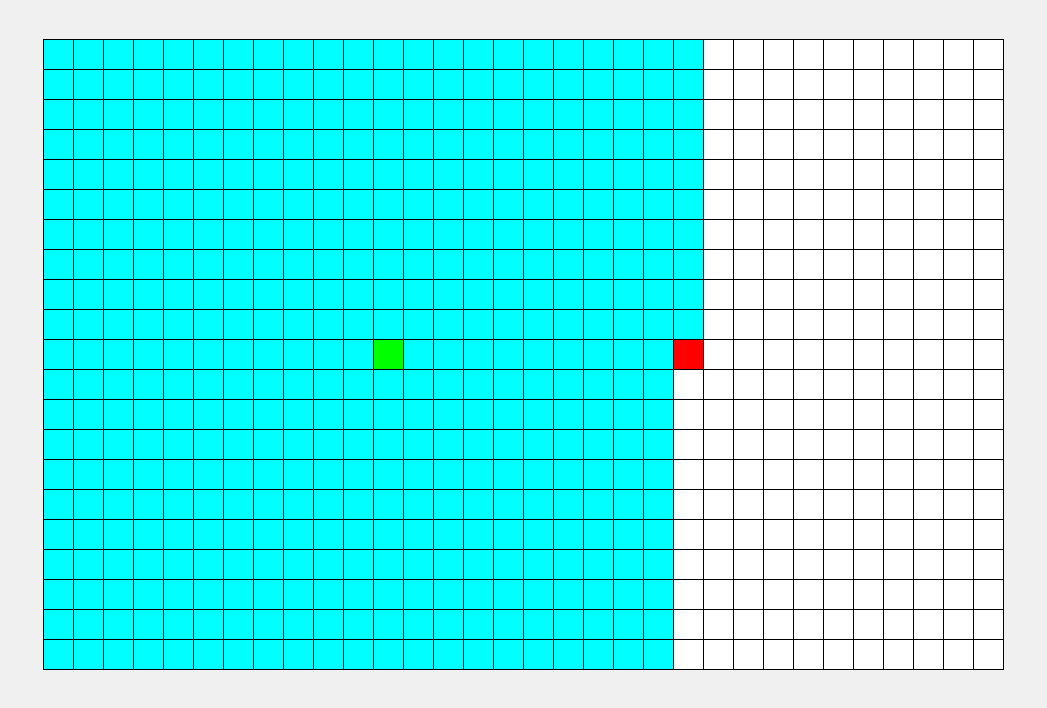（ 图片来源地址 ）
它在搜索树上的搜索顺序如下图

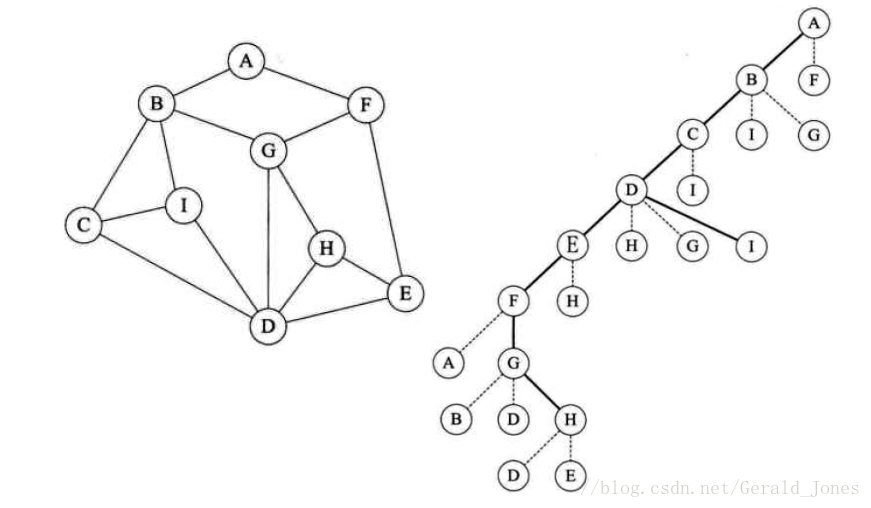
（图片来源地址）

DFS之连通性和搜索顺序

通过DFS算法我们可以用递归的方式从当前状态开始的每个可达状态，如果遍历完后还没有遍历到目标状态，说明开始状态和目标状态不可达。虽然BFS算法也可以做，但搜索空间庞大，而DFS相对就小很多，所以这里推荐使用DFS。

连通性：
例题一
题目链接： 迷宫
题目大意：：判断在一个迷宫里，A点到B点是否可达

• 解析：入门水题。。用来理解算法挺好，用两个数组分别表示纵坐标和横坐标的偏移量，先枚举一个方向，到达往该方向走的位置继续选择一个方向，以此类推，走不通就回溯，回到上一个点，利用循环枚举该点另外一个方向，为了防止走到走过的地方，可以搞一个判重数组，如果走过该点就剪掉
• 时间复杂度:O(地图大小) ,因为要遍历各个点
• 代码实现

#include <iostream>
#include <cstring>
using namespace std;

const int N = 110;

int n;
int sx,sy,ex,ey;
char g[N][N];
bool st[N][N];
int dx[] = {-1,0,1,0} , dy[] = {0,1,0,-1};

bool dfs(int x,int y){
  if(g[x][y] == '#')return false;

  if(x == ex && y == ey)return true;

  st[x][y] = true;
  for(int i = 0 ; i < 4 ; i++)
  {
    int a = x + dx[i] , b = y + dy[i];

    if(a < 0 || a >=n || b < 0 || b >= n)continue;
    if(st[a][b])continue;

    if(dfs(a,b))return true;


  }

  return false;

}

int main(){
  int T;
  cin >> T;

  while(T--)
  {
    cin >> n;

    for(int i = 0 ; i < n ;i++)cin >> g[i];

    memset(st,0,sizeof(st));

    cin >> sx >> sy >> ex >> ey;
    if(dfs(sx,sy))puts("YES");
    else puts("NO");
  }


  return 0;
}

其他例题： 红与黑 ， 马走日

搜索顺序：
例题一
题目链接: 分成互质组
题目大意：把给定分成若干组，使每个组内的元素都互质，问至少可以分多少组

• 题目解析:数据范围较小，所以可以采用暴力DFS。需要考虑的是枚举每个组内的数时要按组合型枚举，防止重复搜索，还有如果下个可以放到已有的组内，就放到组内，不要开新组，显然前者更优，且不影响正确性。

代码部分

#include <iostream>
using namespace std;

const int N = 12;

int n;
int gb[N][10010];
int a[N];
bool st[N];
int ans = N;
int gcd(int a ,int b)
{
    return b ? gcd(b , a % b) : a;
}

bool check(int u,int cnt , int x){

    for(int j = 0 ; j < cnt ;j++)
        if(gcd(gb[u][j] , x) > 1)
             return false;

    return true;
}

void dfs(int g,int gk,int start,int cnt){

    if(g >= ans)return ;
    if(cnt == n)ans = g;
    bool flag = true;

    for(int i = start ; i < n ; i++)
    if(!st[i] && check(g,gk,a[i]))
    {
        st[i] = true;
        gb[g][gk] = a[i] ;
        dfs(g , gk + 1 , i + 1,cnt + 1);
        gb[g][gk] = 0;
        st[i] = false;
        flag = false;
    }
    if(flag)dfs(g + 1 , 0 , 0,cnt) ;
}

int main(){

    cin >> n;

    for(int i = 0 ; i < n ;i++)cin >> a[i];


    dfs(1,0,0 , 0);

    cout << ans << endl;
    return 0;
}

其它例题： 小猫爬山

剪枝

说白了就是优化搜索空间，把搜索空间当做一棵树，把其中不必要的枝叶剪掉，所以形象的被称为“剪枝叶”。

常见的剪枝叶方法：

• 优化搜索顺序：不同的搜索顺序会产生不同的搜索树形态，优先搜索选择 选择少的顺序搜索，规模可以大大减小。
• 排除等效冗余：
• 可行性剪枝：就好比看比看见死胡同，我们会原路返回，即向前扩展到不了想要的，那扩展也没用，就剪掉
• 最优形剪枝：所谓最优性剪枝，是在我们用搜索方法解决最优化问题的时候的一种常用剪枝。就是当你搜到一半的时候，已经比已经搜到的最优解要不优了，那么这个方案肯定是不行的，即刻停止搜索，进行回溯。
• 上下界剪枝：和可行性剪枝类似
• 记忆化：相当于判重。

例题一：
题目链接： 木棍
题目大意：把所给长度不一的木棍拼成若干更长度长度相同的木棍，求可能的最小长度

• 题目解析：考虑几个剪枝
• 1、将所有木棍长从大到小排序一遍，大的取完后还能取到的剩余空间就相对减少，同时也方便其他剪枝；
  2、若当前木棍无法完成拼凑，则与其等长的木棍同样不行，可以跳过；
  3、若木棍X是旧一组的最后一根，旧一组拼完后，发现新一组无法完成，就不需要再枚举比木棍X小的木棍了；
  （因为木棍X是“合适”的，若有比X小的若干木棍能仅仅取代X，但是X却相对那几根木棍的可拼凑种类要少，更不“灵活”，显然不合理）
  4、若在新一组的拼凑中，最大的木棍无法完成，则接下来的这几组都不行（因为那根最长的木棍是迟早要用的）；

代码实现：

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;

const int N = 70;

int len,n,sum,cnt;
int stick[N];
bool st[N];

bool dfs(int u ,int cur,int start){
    if(u > cnt)return true;

    if(cur == len )return dfs(u + 1 , 0 , 1);
    int faliure = -1;
    for(int i = start ; i <= n ;i++)
    if(!st[i] && cur + stick[i] <= len )
    {
        if(faliure == stick[i])continue;
        st[i] = true;

        if(dfs(u , cur + stick[i] , i + 1) ) return true;
        faliure = stick[i];
        st[i] = false;
        if(cur + stick[i] == len || cur == 0)return false;
    }
    return false;
}

int main(){
    while(cin >> n , n)
    {

        int max_len = 0;
        sum = 0;
        for(int i = 1 ; i <= n;i++)
        {
            cin >> stick[i];
            sum += stick[i];
            max_len = max(max_len , stick[i]);
        }

        sort(stick + 1 , stick + n + 1 );
        reverse(stick + 1 , stick + n + 1);


        for(int i = max_len; i <= sum; i++ )
        {
            if(sum % i == 0)
            {
                len = i;
                cnt = sum / len;
                memset(st,false,sizeof(st));
                if(dfs(1 , 0,1)) break;
            }
        }

        cout << len << endl;
    }
 return 0;   
}

例题二
题目链接： 生日蛋糕
题目大意：7月17日是Mr.W的生日，ACM-THU为此要制作一个体积为Nπ的M层生日蛋糕，每层都是一个圆柱体。设从下往上数第i层蛋糕是半径为Ri, 高度为Hi的圆柱。当i < M时，要求Ri > Ri+1且Hi > Hi+1。由于要在蛋糕上抹奶油，为尽可能节约经费，我们希望蛋糕外表面（最下一层的下底面除外）的面积Q最小。令Q = Sπ ，请编程对给出的N和M，找出蛋糕的制作方案（适当的Ri和Hi的值），使S最小。除Q外，以上所有数据皆为正整数 。

• 解析：考虑几个剪枝
• 上下界剪枝叶–设高为h，半径为r，根据圆柱体积公式 和 每层蛋糕的高和半径的递增关系可以得出 r 属于 [dep , min(sqrt(N - V) , r[dep + 1] - 1)] , h 属于 [dep , min((N-V) / r ^ 2 , h[dep + 1] - 1)]
• 优化搜索顺序：采用倒序，即从下往上 。
• 可行性剪枝 ： 如果当前体积加上后面几层的最小体积大于N，就剪掉
• 最优性剪枝：利用h与r数组，dep+1到m层的体积可以表示成n-v=∑（k=dep+1,m）h[k]r[k]r[k]，表面积（不算底面积，因为s先前已经算上了）可以表示成2∑（k=dep+1,m）h[k]r[k]。因为2∑（k=dep+1,m）h[k]r[k]=2/r[dep]∑（k=dep+1,m）h[k]r[k]r[dep]>=2/r[dep]∑（k=dep+1,m）h[k]r[k]r[k]=2(n-v)/r[dep], 所以当s+2(n-v)/r[dep]>=ans时就回溯。

代码实现

#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int N = 22,INF = 1e9;

int n,m,ans = INF;
int r[N] , h[N];
int min_s[N],min_v[N];

void dfs(int u,int s,int v){

    if(s + min_s[u] >= ans)return ;
    if(v + min_v[u] > n)return ;
    if(s + 2 * (n - v) / r[u + 1] >= ans)return ;

    if(u == 0)
    {
        if(v == n)ans = s;
        return ;
    }

    for(int i = min((int)sqrt(n - v) , r[u + 1] - 1) ; i >= u ;i--)
       for(int  j = min((n - v) / i / i  , h[u + 1] - 1); j >= u ;j--)
       {
           int t = 0;
           if(u == m)t = i * i;
           r[u] = i , h[u] = j;
           dfs(u - 1 , s + 2 * i * j + t , v + i * i * j);
       }


}

int main(){

    cin >> n >> m;
    for(int i = 1 ; i <= m ;i++)
    {
        min_s[i] = min_s[i - 1] +  i * i;
        min_v[i] = min_v[i - 1] + i * i * i;
    }

    r[m + 1] = h[m + 1] = 0x3f3f3f3f;
    dfs(m,0,0);
     if (ans == INF) ans = 0;
    cout << ans << endl;
    return 0;
}

双向深搜

问题具有”初态”还有明确的“终态”,那么就可以采用双向搜索分别从初态，和状态各搜索一半状态，产生两棵深度减半的搜索树，在中间交汇就是答案，如果原本的解答树规模是 [a ^ n] ，使用双向搜索后，规模立刻缩小到了约 [a ^ n / 2] ，当 [n] 较大时优化非常可观。。

双向搜索方法

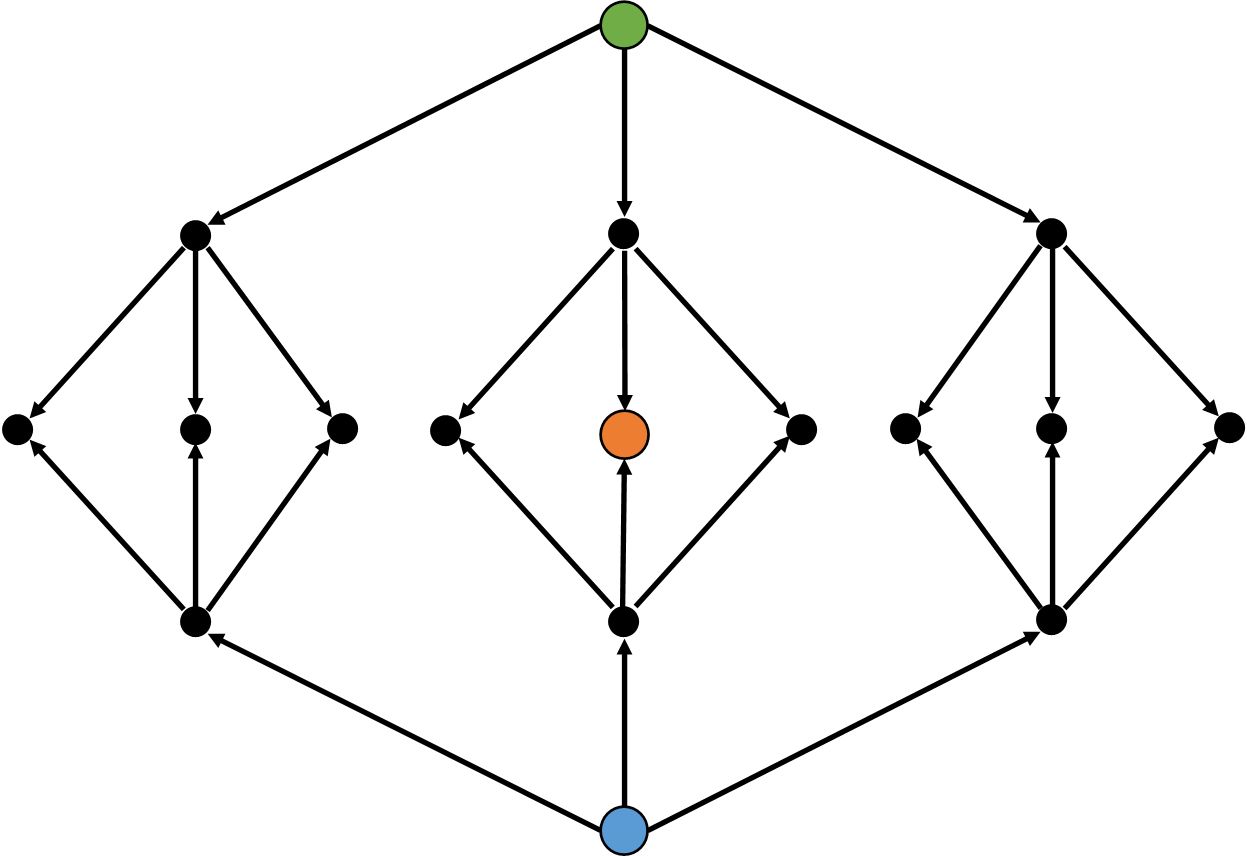
普通搜索方法

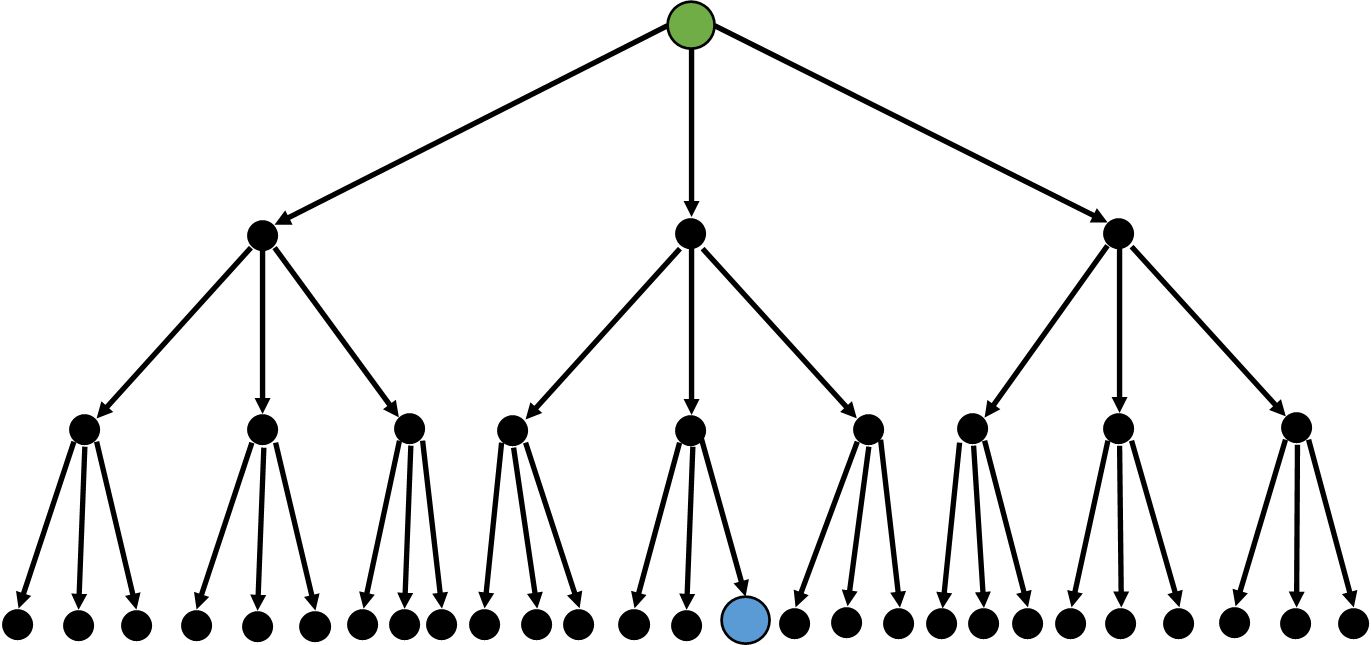
( 图片来源地址 )

例题一
题目链接： 送礼物
题目大意：达达帮翰翰给女生送礼物，翰翰一共准备了N个礼物，其中第i个礼物的重量是G[i]。达达的力气很大，他一次可以搬动重量之和不超过W的任意多个物品。达达希望一次搬掉尽量重的一些物品，请你告诉达达在他的力气范围内一次性能搬动的最大重量是多少。

• 题目解析：这道题看起来像是一个背包问题，但体积非常大，采用DP就自然做不到了，直接解法是“指数型”枚举，每个物品考虑选或是不选，时间复杂度O(2 ^ N) , 而N <= 45 ,s 这明显会炸啊。。。我们可以把所以所有物品分成两块，分别枚举,先枚举前半段礼物，然后排序，去重，在进行第二次搜索,对于每个搜索到的重量值t，从第一部分二分查找 W - t 最大的那个更新答案，时间复杂度为O(2 ^ N / 2 * log 2 ^ N / 2) = O(N * 2 ^ N / 2);

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 1 << 24;

int w,n;
int weight[N] ,g[50];
int k,cnt,ans;

void dfs(int u,int s)
{
    if(u == k)
    {
        weight[cnt++] = s;
        return ;
    }

   if(1ll * s + g[u] <= w)dfs(u + 1 , s + g[u]);
   dfs(u + 1, s);
}

void dfs_girl(int u,int s){
    if(u == n)
    {
        int l = 0 , r = cnt - 1;
        while(l < r )
        {
            int mid = l + r + 1>> 1;
            if(weight[mid] + 1ll * s <= w)l = mid;
            else r = mid - 1;
        }
        if(weight[l] + 1ll * s <= w)ans = max(ans, weight[l] + s);
        return ;
    }

    if(1ll * s + g[u] <= w)dfs_girl(u + 1 , s + g[u]);
    dfs_girl(u + 1 , s);
}
int main(){

    cin >> w >> n;

    for(int i = 0 ; i < n ;i++)cin >> g[i];
    sort(g , g + n ,[](int x,int y){
        return x > y;
    });

    k = n / 2 + 2;

    dfs(0,0);
    sort(weight , weight + cnt);

    int t = 1;

    for(int i = 1 ; i < cnt ; i++)
       if(weight[i] != weight[i - 1])
          weight[t++] = weight[i];

    cnt = t;

    dfs_girl(k , 0);      

    cout << ans;
    return 0;
}

迭代加深和IDA*

迭代加深：每次搜索选定一个分枝，不断深入，直到边界才回溯，是传统的搜索方法，这种方法有很大的缺陷，就是答案在某个很浅的节点，而一开始选错了方向，搜索到了很深的节点上，这浪费大量时间，而且还是无用功，所有当问题明显或者暗示了答案在很浅的范围里，我们就可以从小到大限定一个搜索深度，不断加深，直到搜到答案，这个过程虽然会导致重复搜索，但相对于深层子树的规模来说，就是小巫见大巫了。

假设问题的搜索树如下，其实后面还有很多节点：

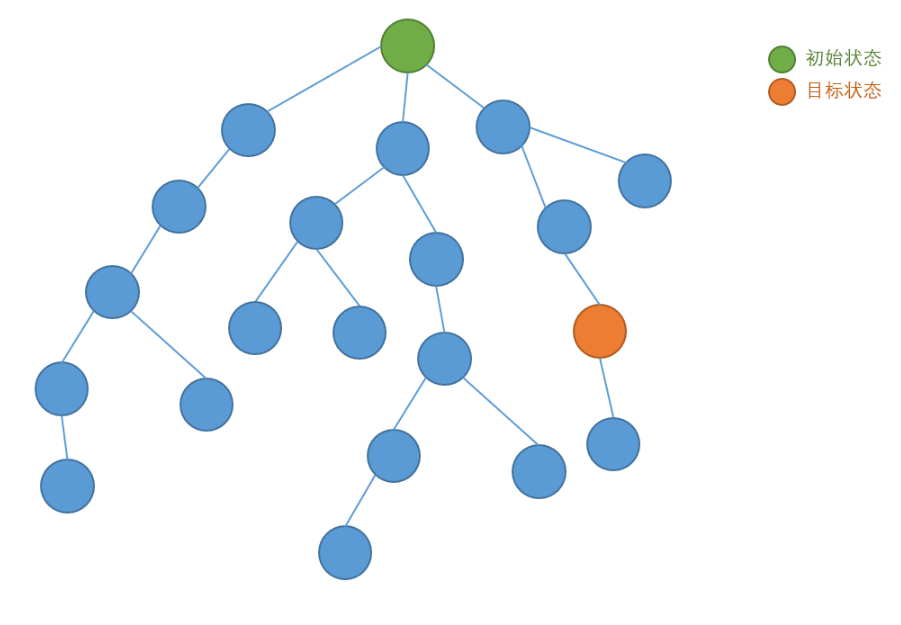
按照迭代加深的思路，限制一个搜索深度，不断加深，直到找到答案

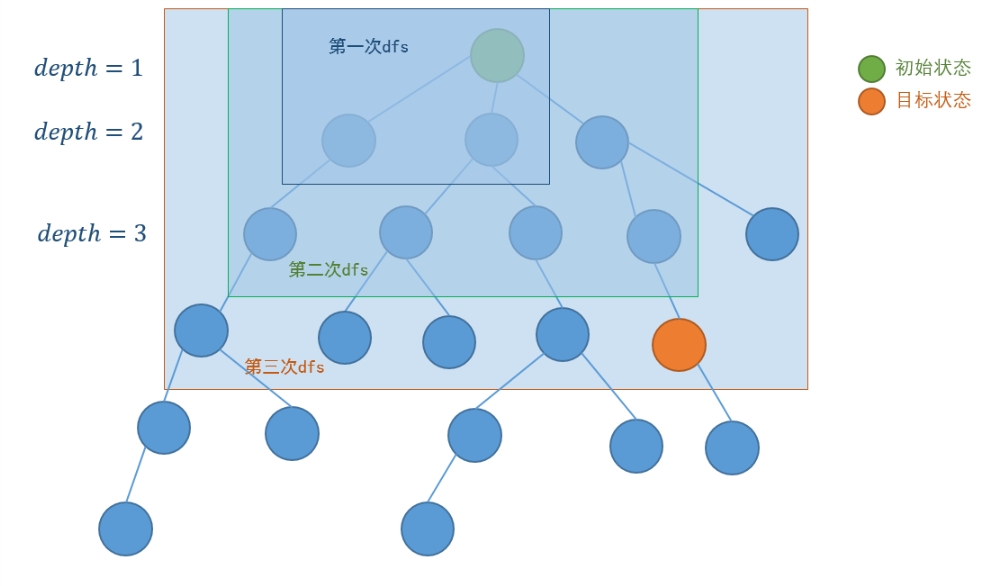
（ 图片来源地址 ）

例题
题目地址： 加成序列
题目大意：满足如下条件的序列X（序列中元素被标号为1、2、3…m）被称为“加成序列”：
1、X[1]=1
2、X[m]=n
3、X[1]<X[2]<…<X[m-1]<X[m]
4、对于每个 k（2≤k≤m）都存在两个整数 i 和 j （1≤i,j≤k−1，i 和 j 可相等），使得X[k]=X[i]+X[j]。
你的任务是：给定一个整数n，找出符合上述条件的长度m最小的“加成序列”。
如果有多个满足要求的答案，只需要找出任意一个可行解。

• 解析：依次搜索每个位置k，枚举i， j （前面两个数）作为分支，把x[i] + x[j] 填到 x[k]上，然后不懂加深； 除此之外还有考虑两个剪枝 1 ，优化搜索顺序：为了尽快逼近答案，优先选择 可以扩展余地少的顺序，即从大到小枚举 x[i] ， x[j] 2 , 排除等效冗余 ： 对于不同的 i， j ,x[i] + x[j] 可能是相等的，可以用一个判重数组，避免重复搜索.

代码实现：

#include <iostream>
using namespace std;

const int N = 112;

int deg,n;
int path[N];


bool dfs(int u,int d){

     if(u == d)return path[u - 1] == n;

     bool st[N] = {0};
     for(int i = u - 1 ;i >= 0 ; i--)
        for(int j = i ; j >= 0 ; j--)
        {
            int s = path[i] + path[j];
            if( s > n ||s <= path[u - 1]||st[s] )continue;
            st[s] = true;
            path[u] = s; 
            if(dfs(u + 1 , d))return true;
        }
    return false;
}

int main(){
    path[0] = 1;
    while(cin >> n  , n)
    {
        deg = 1;
        while(!dfs(1 , deg))deg++;

        for(int i = 0 ; i < deg ; i++)cout << path[i] << ' ';
        cout << endl;
    }

    return 0;
}

IDA*

其实就是在迭代加深的基础上增加了一个估价函数 ，把原来的限制改为： 若当前深度加未来估计步数 > 深度限制 就回溯 ，就变成了启发式搜索，也可以当做是一个剪枝优化吧 ， IDA* 算法的效率主要是根据估价函数。

• 解析： yxc大佬的题解
  代码实现：

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 16;

int n;
int step;
int book[N];
int w[5][N];

int f(){
    int tot = 0;
    for(int i = 1 ; i < n ;i++)
      if(book[i]!= book[i - 1] + 1)
          tot++;

    return ( tot + 2 ) / 3;
}

bool check(){
    for(int i = 1 ; i < n ;i++)
       if(book[i] != i + 1 )
           return false;

   return true;
}

bool dfs(int depth,int maxdepth)
{
    if(depth + f()> maxdepth)return false;
    if(check())return true;

    for(int l = 0 ; l < n ; l++)
      for(int r = l ; r < n ;r++)
         for(int k = r + 1 ; k < n ;k ++)
         {
             memcpy(w[depth], book, sizeof(book));
             int x,y;
             for(x = r + 1 ,y = l ; x <= k ; x++ , y++)book[y] = w[depth][x];
             for(x = l ; x <= r ;x++,y++)book[y] = w[depth][x];
             if(dfs(depth + 1 , maxdepth))return true;
             memcpy(book,w[depth],sizeof(w[depth]));
         }
    return false;
}

int main(){

    int T;
    cin >> T;
    while(T--)
    {
        cin >> n;

        for(int i = 0 ; i < n ;i++)cin >> book[i];
        step = 0;    
       while(!dfs(0 , step) && step <= 4)step++;

        if(step > 4 )cout << "5 or more" <<endl;
        else cout << step << endl;

    }
    return 0;
}

例题二
题目链接： 回转游戏
题目大意：如下图所示，有一个“#”形的棋盘，上面有1,2,3三种数字各8个。
给定8种操作，分别为图中的A~H。
这些操作会按照图中字母和箭头所指明的方向，把一条长为8的序列循环移动1个单位。
例如下图最左边的“#”形棋盘执行操作A后，会变为下图中间的“#”形棋盘，再执行操作C后会变成下图最右边的“#”形棋盘。
给定一个初始状态，请使用最少的操作次数，使“#”形棋盘最中间的8个格子里的数字相同。

• 解析： yxc大佬的题解

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 24;

int op[8][7] = {
    0,2,6,11,15,20,22,
    1,3,8,12,17,21,23,
    10,9,8,7,6,5,4,
    19,18,17,16,15,14,13,
    23,21,17,12,8,3,1,
    22,20,15,11,6,2,0,
    13,14,15,16,17,18,19,
    4,5,6,7,8,9,10
};

int rop[8] = {5,4,7,6,1,0,3,2};
int center[8] = {6, 7, 8, 11, 12, 15, 16, 17};
int path[100];
int q[N];

int f()
{
    static int sum[4];
    memset(sum, 0, sizeof sum);
    for (int i = 0; i < 8; i ++ ) sum[q[center[i]]] ++ ;

    int s = 0;
    for (int i = 1; i <= 3; i ++ ) s = max(s, sum[i]);
    return 8 - s;
}

bool check()
{
    for (int i = 1; i < 8; i ++ )
        if (q[center[i]] != q[center[0]])
            return false;
    return true;
}

void operation(int x)
{
    int t = q[op[x][0]];
    for (int i = 0; i < 6; i ++ ) q[op[x][i]] = q[op[x][i + 1]];
    q[op[x][6]] = t;
}



bool dfs(int depth, int max_depth, int last)
{
    if (depth + f() > max_depth) return false;
    if (check()) return true;

    for (int i = 0; i < 8; i ++ )
    {
        if (rop[i] == last) continue;
        operation(i);
        path[depth] = i;
        if (dfs(depth + 1, max_depth, i)) return true;
        operation(rop[i]);
    }

    return false;
}




int main(){

     while (scanf("%d", &q[0]), q[0])
    {
        for (int i = 1; i < N; i ++ ) scanf("%d", &q[i]);
        int depth = 0;
        while (!dfs(0, depth, -1))
        {
            depth ++ ;
        }
        if (!depth) printf("No moves needed");
        for (int i = 0; i < depth; i ++ ) printf("%c", 'A' + path[i]);
        printf("\n%d\n", q[6]);
    }

    return 0;
}

例题三
题目链接： 玛雅游戏
题目大意：如题

• 解析： yxc大佬的题解

#include <iostream>
#include <cstring>
using namespace std;

struct Path{
    int x,y,d;
}path[10];

int n;
int map[10][10],bmap[5][10][10];
int cnt[11],bcnt[5][10];
bool st[11][11];

void move(int x,int y,int nx){

    swap(map[x][y] , map[nx][y]);

    while(true){
        bool flag = false;

        for(int i = 0 ; i < 5 ;i++)
        {
            int k = 0;
            for(int j = 0; j < 7 ;j++)
              if(map[i][j])
                 map[i][k++] = map[i][j];

            while(k < 7)map[i][k++] = 0;     
        }
          memset(st, 0, sizeof st);
        for(int i = 0 ; i < 5 ; i++)
           for(int j = 0 ; j < 7 ; j++)
           if(map[i][j])
           {
               int l = i , r = i; 
               while(l - 1 >= 0 && map[l - 1][j] == map[i][j])l--;
               while(r + 1 < 5 && map[r + 1][j] == map[i][j])r++;
               if(r - l + 1 >= 3)
               {
                   st[i][j] = true;
                   flag = true;
               }
               else
               {
                   int l = j,r = j;
                   while(l - 1>= 0 && map[i][l - 1] == map[i][j])l--;
                   while(r + 1 < 7 && map[i][r + 1] == map[i][j])r++;
                   if(r - l + 1 >= 3)
                   {
                       st[i][j] = true;
                       flag = true;
                   }
               }
           }

        if(!flag)break;
        for(int i = 0 ; i < 5 ;i++)
           for(int j = 0 ; j < 7 ; j++)
           if(st[i][j])
           {

               cnt[map[i][j]]--;
               cnt[0]--;
               map[i][j] = 0;
           }

    }
}

bool dfs(int u )
{
    if(u == n)return !cnt[0];

    for(int i = 1 ; i <= 10 ;i++)
        if(cnt[i] ==2 || cnt[i] == 1)
            return false;

    memcpy(bcnt[u],cnt,sizeof(cnt));
    memcpy(bmap[u],map,sizeof(map));
    for(int i = 0 ; i < 5 ;i++)
      for(int j = 0 ; j < 7 ; j++)
      if(map[i][j])
      {
          int nx = i + 1;

          if(nx < 5 )
          {
              path[u] = {i , j , 1};
              move(i,j,nx);
              if(dfs(u + 1))return true;
              memcpy(cnt,bcnt[u], sizeof(bcnt[u]));
              memcpy(map,bmap[u],sizeof(bmap[u]));
          }

          nx = i - 1;
          if(nx >= 0 && !map[i - 1][j])
          {
              path[u] = {i , j , -1};
              move(i,j,nx);
              if(dfs(u + 1))return true;
              memcpy(cnt,bcnt[u], sizeof(bcnt[u]));
              memcpy(map,bmap[u],sizeof(bmap[u]));
          }
      }

     return false;
}

int main(){

    cin >> n;

    for(int i = 0 ,t = 0; i < 5 ;i++)
    {
        int y = 0;
        while(scanf("%d",&t),t)
        {
            cnt[0] ++;
            cnt[t]++;
            map[i][y++] = t;
        }

    }

    if(dfs(0))
    {
        for(int i = 0 ; i < n ;i++)
        cout << path[i].x << ' '<<path[i].y << ' '<<path[i].d << endl;
    }
    else cout << -1 << endl;

    return 0;
}