区间DP
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
s = ' ' + s;
int f[n + 1][n + 1];
memset(f, 0, sizeof f);
int mxl = 0, st = -1;
for (int len = 1; len <= n; ++len) {
for (int i = 1; i + len - 1 <= n; ++i) {
int j = i + len - 1;
if (len <= 2) f[i][j] = s[i] == s[j] ? len : 0;
else {
if (s[i] == s[j] && f[i + 1][j - 1]) f[i][j] = len;
}
if (f[i][j] > mxl) {
mxl = f[i][j];
st = i;
}
}
}
return s.substr(st, mxl);
}
};
双串匹配 + 线性dp
2种字符:
(1).a~z
(2)[.(a~z)]*两个字符作为一个整体
- 整体的思想,通过推公式减少一维匹配个数的遍历

- 分开看是无法化简的
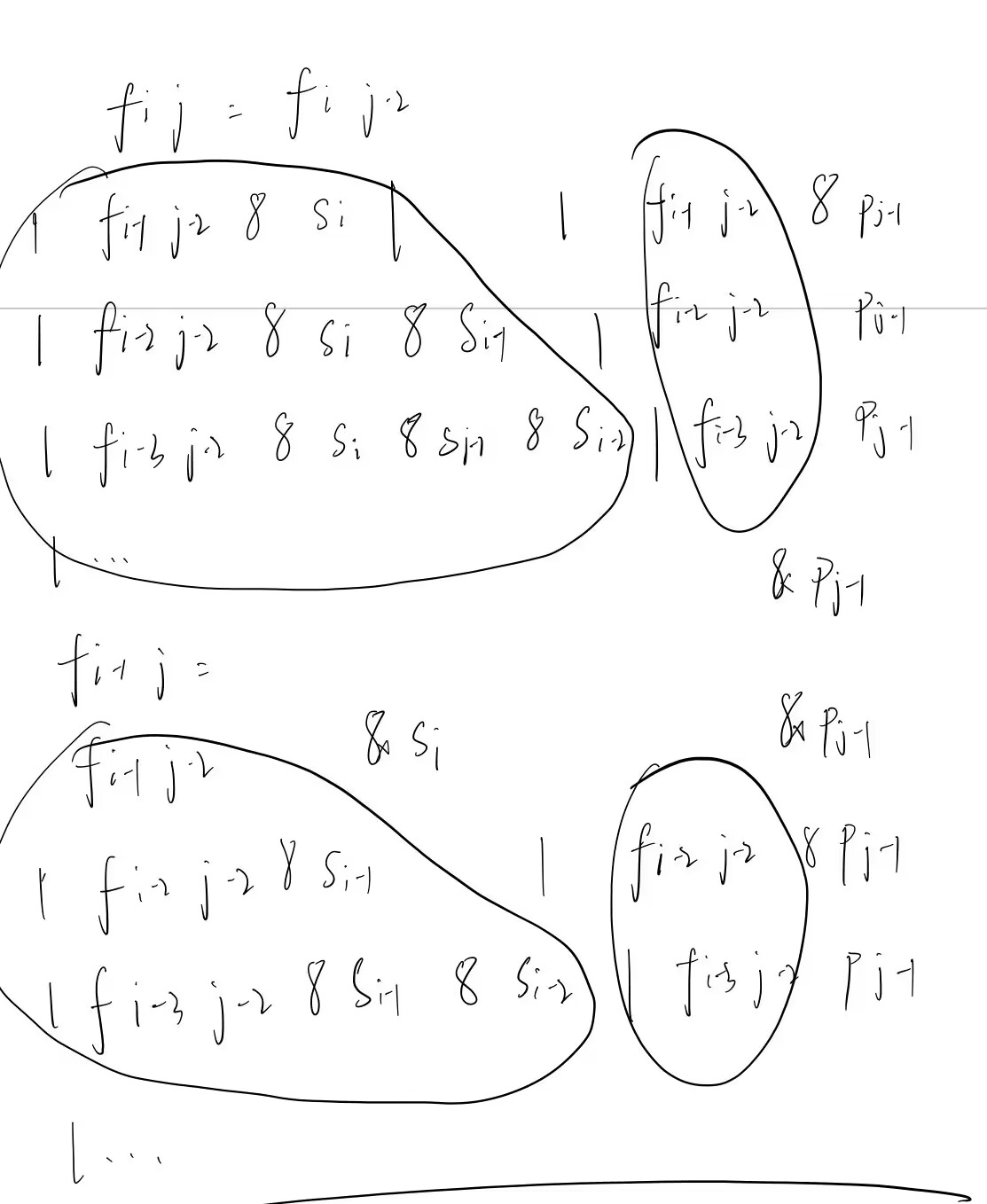
class Solution {
public:
bool isMatch(string s, string p) {
int n = s.size(), m = p.size();
s = ' ' + s, p = ' ' + p;
vector<vector<bool>> f(n + 1, vector<bool>(m + 1));
f[0][0] = true;
for (int i = 0; i <= n; ++i)
for (int j = 1; j <= m; ++j) {
if (j + 1 <= m && p[j + 1] == '*') continue; // 当前字符尚未结束
if (p[j] != '*') {
if (i) { // 第一种字符一定不能匹配0个
f[i][j] = f[i - 1][j - 1] && (s[i] == p[j] || p[j] == '.');
}
} else {
f[i][j] = f[i][j - 2]; // 匹配数为0 这里不受i影响不需要特判直接赋值
if (i) { // 推公式
f[i][j] = f[i][j] || f[i - 1][j] && (s[i] == p[j - 1] || p[j - 1] == '.'); // 注意是j - 1
}
}
}
return f[n][m];
}
};
线性dp + 括号匹配
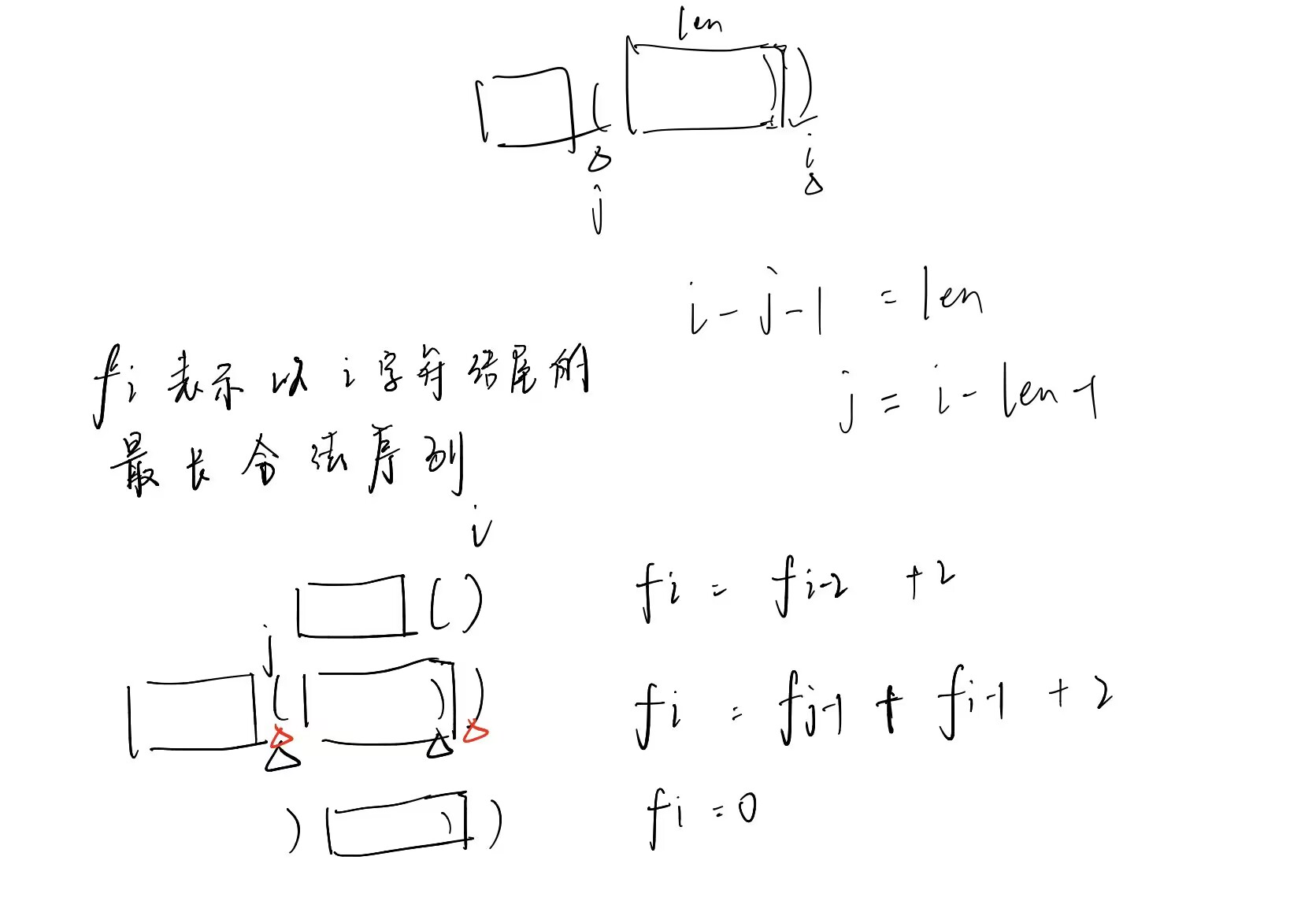
class Solution {
public:
int longestValidParentheses(string s) {
int n = s.size();
s = ' ' + s;
int ans = 0;
int f[n + 1];
memset(f, 0, sizeof f);
for (int i = 2; i <= n; ++i) {
if (s[i] == '(') continue;
if (s[i] == ')') {
if (s[i - 1] == '(') f[i] = f[i - 2] + 2;
else if (s[i - f[i - 1] - 1] == '(') {
int j = i - f[i - 1] - 1;
f[i] = f[j - 1] + f[i - 1] + 2;
}
}
ans = max(ans, f[i]);
}
return ans;
}
};
线性DP
class Solution {
public:
int jump(vector<int>& nums) {
int n = nums.size();
vector<int> f(n);
f[0] = 0;
for (int last = 0, i = 1; i < n; ++i) {
while (last + nums[last] < i) last++; // j > i, f[j] >= f[i], 尝试用最左的位置更新
f[i] = f[last] + 1;
}
return f[n - 1];
}
};
以i为结尾定义的线性灯泡
class Solution {
public:
int maxSubArray(vector<int>& nums) {
int n = nums.size();
vector<int> f(n);
int ans = f[0] = nums[0];
for (int i = 1; i < n; ++i) {
f[i] = max(0, f[i - 1]) + nums[i];
ans = max(ans, f[i]);
}
return ans;
}
};
初始化
class Solution {
public:
int uniquePaths(int m, int n) {
int f[m + 1][n + 1];
memset(f, 0, sizeof f);
f[0][1] = 1; // 初始化
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j)
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
return f[m][n];
}
};
初始化
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& g) {
if (g[0][0]) return 0;
int n = g.size(), m = g[0].size();
int f[n + 1][m + 1];
memset(f, 0, sizeof f);
f[0][1] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (g[i - 1][j - 1]) continue;
f[i][j] = f[i - 1][j] + f[i][j - 1];
}
}
return f[n][m];
}
};
初始化
class Solution {
public:
int minPathSum(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
int f[n + 1][m + 1];
memset(f, 0x3f, sizeof f);
f[1][0] = 0; // 初始化
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
f[i][j] = min(f[i - 1][j], f[i][j - 1]) + g[i - 1][j - 1];
}
return f[n][m];
}
};
初始化 + 双串匹配
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size();
word1 = ' ' + word1, word2 = ' ' + word2;
int f[n + 1][m + 1];
memset(f, 0x3f, sizeof f);
for (int i = 0; i <= n; ++i) f[i][0] = i;
for (int j = 0; j <= m; ++j) f[0][j] = j;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j)
if (word1[i] == word2[j]) f[i][j] = f[i - 1][j - 1];
else f[i][j] = min({f[i - 1][j - 1], f[i - 1][j], f[i][j - 1]}) + 1;
}
return f[n][m];
}
};
区间dp
- f[i][j][len]表示s1[i ~ i+len-1]与s2[j ~ j+len-1]的匹配集合
class Solution {
public:
bool isScramble(string s1, string s2) {
int n = s1.size();
bool f[n][n][n + 1];
memset(f, 0, sizeof f);
for (int len = 1; len <= n; ++len) {
for (int i = 0; i + len - 1 < n; ++i) {
for (int j = 0; j + len - 1 < n; ++j) {
if (len == 1) f[i][j][len] = s1[i] == s2[j];
else
for (int k = 1; k < len; ++k) {
if ((f[i][j][k] && f[i + k][j + k][len - k])
|| (f[i][j + len - k][k] && f[i + k][j][len - k])) {
f[i][j][len] = true;
break; // 找到合法的分割方式则退出
}
}
}
}
}
return f[0][0][n];
}
};
线性dp
class Solution {
public:
int numDecodings(string s) {
int n = s.size();
s = ' ' + s;
vector<int> f(n + 1);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
// if (i >= 2) {
int v = stoi(s.substr(i - 1, 2));
if (10 <= v && v <= 26) f[i] += f[i - 2]; // 两位解码
// }
if (s[i] > '0') f[i] += f[i - 1]; // 一位解码
}
return f[n];
}
};
二叉搜索树形态 + 树形dp
class Solution {
public:
int numTrees(int n) {
vector<int> f(n + 1);
f[0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j < i; ++j) {
f[i] += f[j] * f[i - 1 - j];
}
}
return f[n];
}
};
双串匹配第三个串
- f[i][j]表示s1[1 ~ i]和s2[1 ~ j]匹配s3[1 ~ i+j]的所有集合
- 根据s3[i + j]匹配情况划分集合
class Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int n1 = s1.size(), n2 = s2.size();
if (n1 + n2 != s3.size()) return false;
bool f[n1 + 1][n2 + 1];
memset(f, 0, sizeof f);
s1 = ' ' + s1, s2 = ' ' + s2, s3 = ' ' + s3;
for (int i = 0; i <= n1; ++i) {
for (int j = 0; j <= n2; ++j) {
if (!i && !j) f[0][0] = true;
else {
if (s1[i] == s3[i + j]) f[i][j] |= f[i - 1][j]; // 这里不需要判断i > 0,s1[0] != s3[i + j]
if (s2[j] == s3[i + j]) f[i][j] |= f[i][j - 1];
}
}
}
return f[n1][n2];
}
};
双串子序列匹配
- f[i][j]表示s[1~i]中匹配t[1~j]子序列的集合
- 根据s[i]与t[j]匹配与否划分
- s[i] != t[j]只能f[i - 1][j]转移
- s[i] == t[j]可以选择匹配也可以不匹配f[i - 1][j - 1] + f[i - 1][j]
class Solution {
public:
int numDistinct(string s, string t) {
int n = s.size(), m = t.size();
s = ' ' + s, t = ' ' + t;
unsigned long long f[n + 1][m + 1];
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= m; ++j) {
f[i][j] = f[i - 1][j];
if (j && s[i] == t[j]) f[i][j] += f[i - 1][j - 1];
}
}
return f[n][m];
}
};
记忆化自顶向下搜索
class Solution {
public:
int minimumTotal(vector<vector<int>>& g) {
int n = g.size();
int f[n][n];
memset(f, -1, sizeof f);
function<int(int, int)> dp = [&](int u, int c) -> int {
if (u == n - 1) return g[u][c];
if (~f[u][c]) return f[u][c];
int res = min(dp(u + 1, c), dp(u + 1, c + 1)) + g[u][c];
f[u][c] = res;
return res;
};
return dp(0, 0);
}
};
状态机DP – 不限交易次数
class Solution {
public:
int maxProfit(vector<int>& p) {
int n = p.size();
// int f[n + 1][2];
int f[2][2];
memset(f, 0xcf, sizeof f);
f[0 & 1][0] = 0;
for (int i = 1; i <= n; ++i) {
f[i & 1][0] = max(f[i - 1 & 1][0], f[i - 1 & 1][1] + p[i - 1]);
f[i & 1][1] = max(f[i - 1 & 1][1], f[i - 1 & 1][0] - p[i - 1]);
}
return f[n & 1][0];
}
};
前后缀分离dp
- 只记录前缀信息,后缀信息边计算边处理
class Solution {
public:
int maxProfit(vector<int>& p) {
int n = p.size();
vector<int> f(n + 1); // f[i]表示前i天最多只做一笔交易所获最大利润
int mn = p[0]; // 记录最小买入价格
for (int i = 1; i <= n; ++i) {
f[i] = max(f[i - 1], p[i - 1] - mn); // f[i - 1] >= 0, 所以不必特判p[i - 1] - mn
mn = min(mn, p[i - 1]);
}
int ans = 0, mx = p[n - 1]; // 记录最大卖出价格
for (int i = n; i >= 1; --i) {
// int v = max(0, mx - p[i - 1]); 更好理解一些
int v = mx - p[i - 1]; // 这样正确的原因是最多两笔交易, v < 0的情况会被只做一笔交易优化掉
ans = max(ans, f[i - 1] + v);
mx = max(mx, p[i - 1]);
}
return ans;
}
};
树形DP
- 树中的路径问题
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int maxPathSum(TreeNode* root) {
int ans = -1e9;
function<int(TreeNode*)> dfs = [&](TreeNode* u) -> int {
if (!u) return 0;
int res = u->val;
int lv = max(0, dfs(u->left));
int rv = max(0, dfs(u->right));
ans = max(ans, res + lv + rv);
res += max(lv, rv);
return res;
};
dfs(root);
return ans;
}
};
dp预处理回文串
class Solution {
public:
vector<vector<string>> partition(string s) {
int n = s.size();
s = ' ' + s;
int f[n + 1][n + 1];
memset(f, 0, sizeof f);
for (int len = 1; len <= n; ++len) {
for (int i = 1; i + len - 1 <= n; ++i) {
int j = i + len - 1;
if (len <= 2) f[i][j] = s[i] == s[j];
else f[i][j] = f[i + 1][j - 1] & (s[i] == s[j]);
}
}
vector<vector<string>> ans;
function<void(int, vector<string>)> dfs = [&](int u, vector<string> path) {
if (u > n) {
ans.emplace_back(path);
return ;
}
for (int i = u; i <= n; ++i) {
if (f[u][i] == false) continue;
path.emplace_back(s.substr(u, i - u + 1));
dfs(i + 1, path);
path.pop_back();
}
};
vector<string> path;
dfs(1, path);
return ans;
}
};
区间dp + 线性dp + 初始化
- 最少分割次数通过最少回文段数 - 1求得
class Solution {
public:
int minCut(string s) {
int n = s.size();
s = ' ' + s;
bool st[n + 1][n + 1];
memset(st, 0, sizeof st);
for (int len = 1; len <= n; ++len) {
for (int i = 1; i + len - 1 <= n; ++i) {
int j = i + len - 1;
if (len <= 2) st[i][j] = s[i] == s[j];
else st[i][j] = st[i + 1][j - 1] & (s[i] == s[j]);
}
}
int f[n + 1];
iota(f, f + n + 1, 0); // 最多单个字符一段
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
if (st[j][i])
f[i] = min(f[i], f[j - 1] + 1);
}
}
return f[n] - 1;
}
};
线性dp
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
int n = s.size(), mxl = 0;
unordered_set<string> S;
for (auto &word : wordDict) {
mxl = max(mxl, (int)word.size());
S.emplace(word);
}
s = ' ' + s;
bool f[n + 1];
memset(f, 0, sizeof f);
f[0] = true;
for (int i = 1; i <= n; ++i) {
for (int len = 1; len <= min(i, mxl); ++len) {
int x = i - len + 1;
f[i] |= f[x - 1] & S.count(s.substr(x, len));
}
}
return f[n];
}
};
dfs(本题不是dp题)
class Solution {
public:
vector<string> wordBreak(string s, vector<string>& wordDict) {
int n = s.size(), mxl = 0;
unordered_set<string> S;
for (auto &word : wordDict) {
S.emplace(word);
mxl = max(mxl, (int)word.size());
}
vector<string> ans;
function<void(int, string)> dfs = [&](int u, string path) {
if (u == n) {
path.pop_back();
ans.emplace_back(path);
return ;
}
for (int len = 1; u + len - 1 < n; ++len) {
string str = s.substr(u, len);
if (S.count(str)) {
int j = u + len;
dfs(j, path + str + ' ');
}
}
};
dfs(0, "");
return ans;
}
};
二分 + 网格dp
class Solution {
public:
int calculateMinimumHP(vector<vector<int>>& g) {
int n = g.size(), m = g[0].size();
int f[n + 1][m + 1];
int l = 1, r = 400 * 1000;
while (l <= r) {
int mid = l + r >> 1;
function<bool(int)> check = [&](int x) -> bool {
memset(f, 0xcf, sizeof f);
f[0][1] = x;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) { // 需要上一步状态血量> 0
if (f[i - 1][j] > 0) f[i][j] = max(f[i][j], f[i - 1][j] + g[i - 1][j - 1]);
if (f[i][j - 1] > 0) f[i][j] = max(f[i][j], f[i][j - 1] + g[i - 1][j - 1]);
}
}
return f[n][m] > 0;
};
if (check(mid)) r = mid - 1;
else l = mid + 1;
}
return r + 1;
}
};
class Solution {
public:
int maxProfit(int k, vector<int>& p) {
int n = p.size();
int f[n + 1][k + 1][2];
memset(f, 0xcf, sizeof f);
f[0][0][0] = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 0; j <= k; ++j) {
f[i][j][0] = max(f[i - 1][j][0], f[i - 1][j][1] + p[i - 1]);
f[i][j][1] = f[i - 1][j][1];
if (j) f[i][j][1] = max(f[i][j][1], f[i - 1][j - 1][0] - p[i - 1]);
}
}
int ans = 0;
for (int j = 0; j <= k; ++j) ans = max(ans, f[n][j][0]);
return ans;
}
};
线性dp
- f[i][0]表示1~i天第i天不偷窃所能获得的最大收益
- f[i][1]表示1~i天第i天偷窃所能获得的最大收益
class Solution {
public:
int rob(vector<int>& nums) {
int n = nums.size();
int f[n + 1][2];
memset(f, 0xcf, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; ++i) {
f[i][0] = max(f[i - 1][0], f[i - 1][1]);
f[i][1] = f[i - 1][0] + nums[i - 1]; // 前一天只能是不偷窃
}
return max(f[n][0], f[n][1]);
}
};

