kruskal算法

kruskal算法的2个关键技术：

（1）对边进行排序。

（2）判断圈，即处理连通性问题。这个问题用并查集简单而高效，并查集是kruskal算法的绝配。

kruskal算法步骤

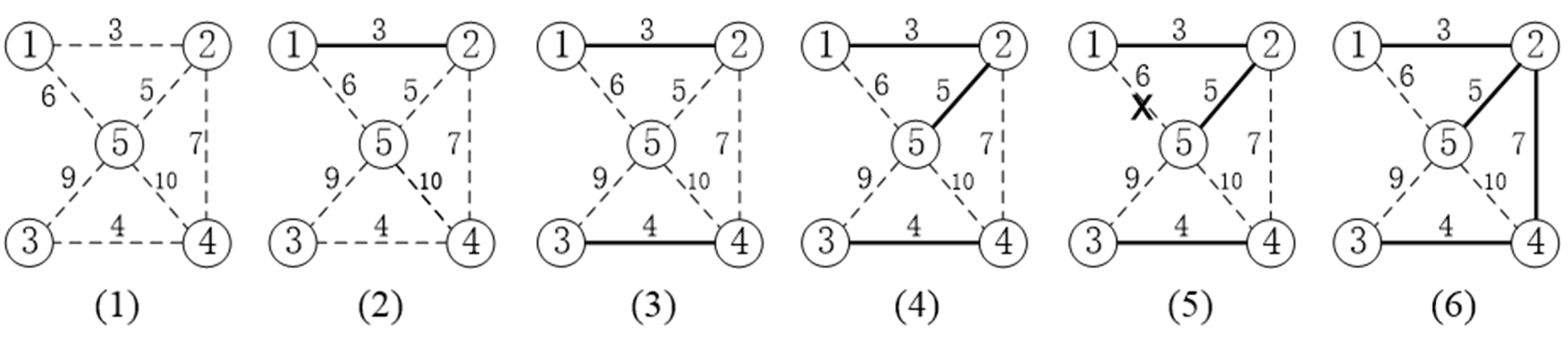
（1）初始时最小生成树T为空。令S是以结点i为元素的并查集，开始的时候，每个点属于独立的集。

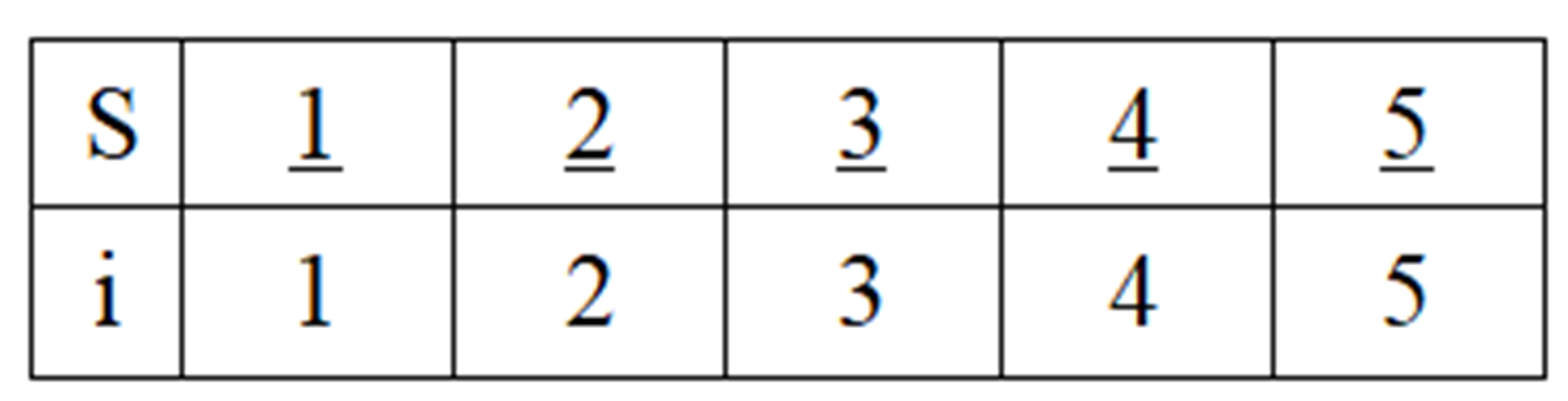
（2）加入第一个最短边(1-2)：T={1-2}。并查集S中，把结点2合并到结点1，也就是把结点2的集2改成结点1的集1。

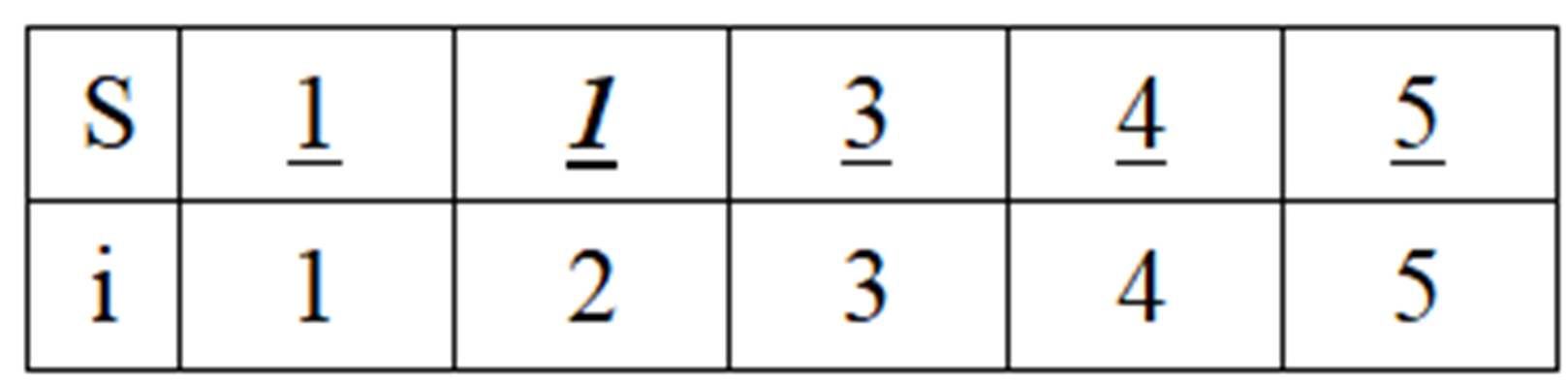
（3）加入第二个最短边(3-4)：T={1-2, 3-4}。并查集S中，结点4合并到结点3。

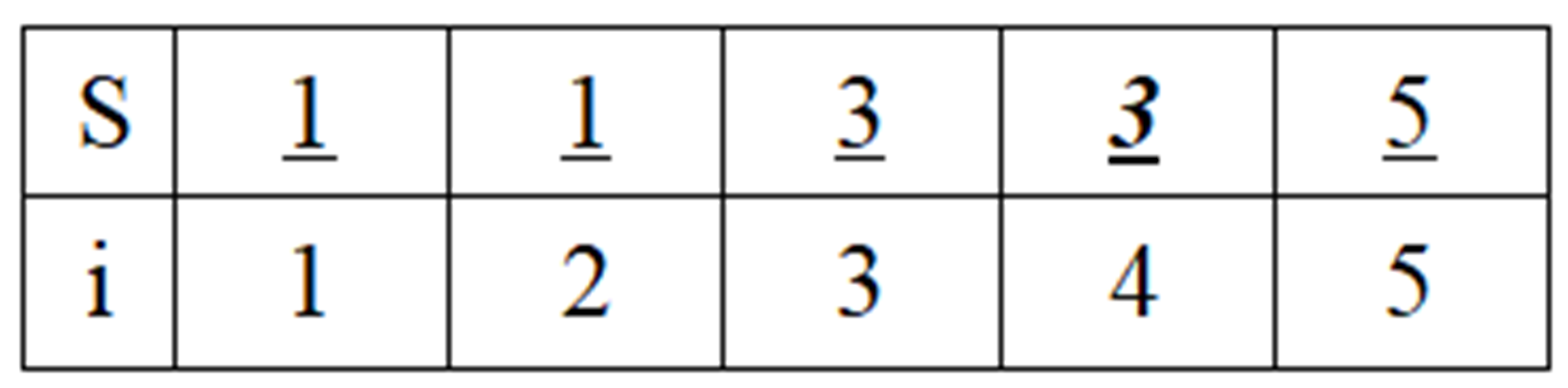
（4）加入第三个最短边(2-5)：T={1-2, 3-4, 2-5}。并查集S中，把结点5合并到结点2，也就是把结点5的集5改成结点2的集1。在集1中，所有结点都指向了根结点，这样做能避免并查集的长链问题。即使用了“路径压缩”的方法。

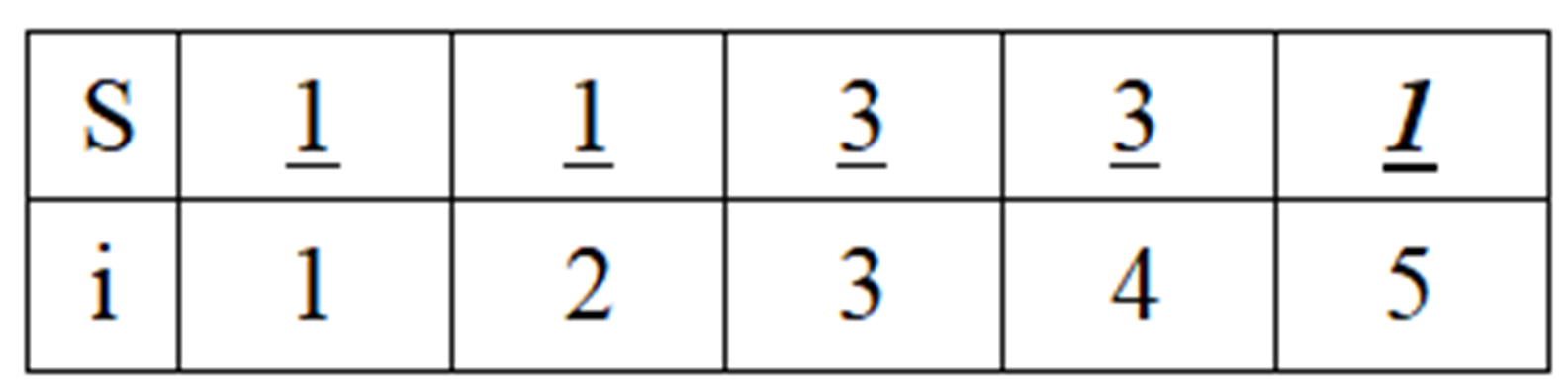
（5）第四个最短边(1-5)。检查并查集S，发现5已经属于集1，丢弃这个边。这一步实际上是发现了一个圈。并查集的作用就体现在这里。

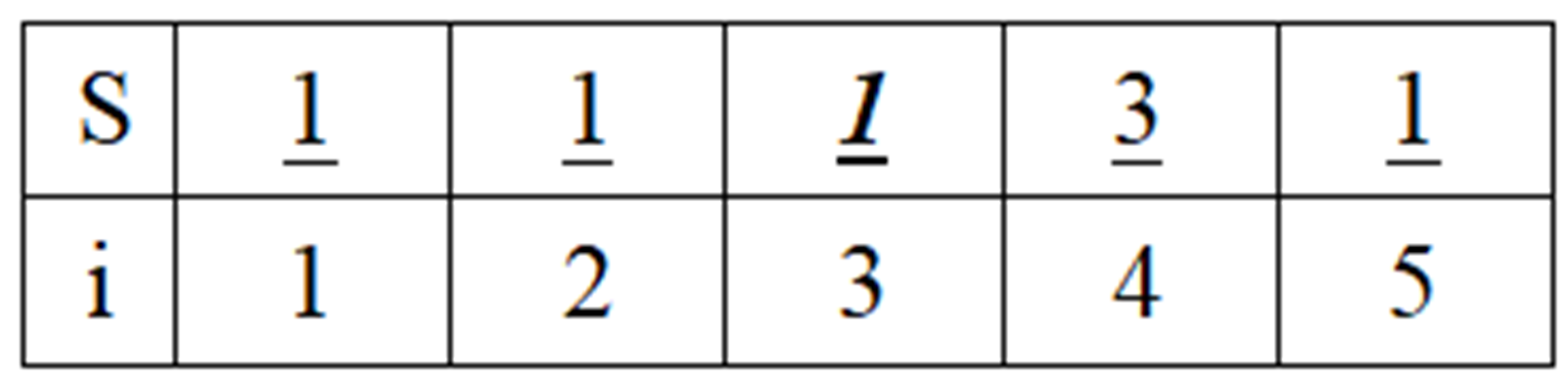
（6）加入第五个最短边(2-4)。并查集S中，把结点4的集并到结点2的集。注意这里结点4原来属于集3，实际上修改的是：把结点3的集3改成1。

kruskal算法复杂度

• kruskal算法的复杂度包括两部分：对边的排序O(ElogE)，并查集的操作O(E)，一共是O(ElogE + E)，约等于O(ElogE)，时间主要花在排序上。
• 如果图的边很多，kruskal的复杂度要差一些。
• kruskal适用于稀疏图，prim适合稠密图。