更好的阅读体验

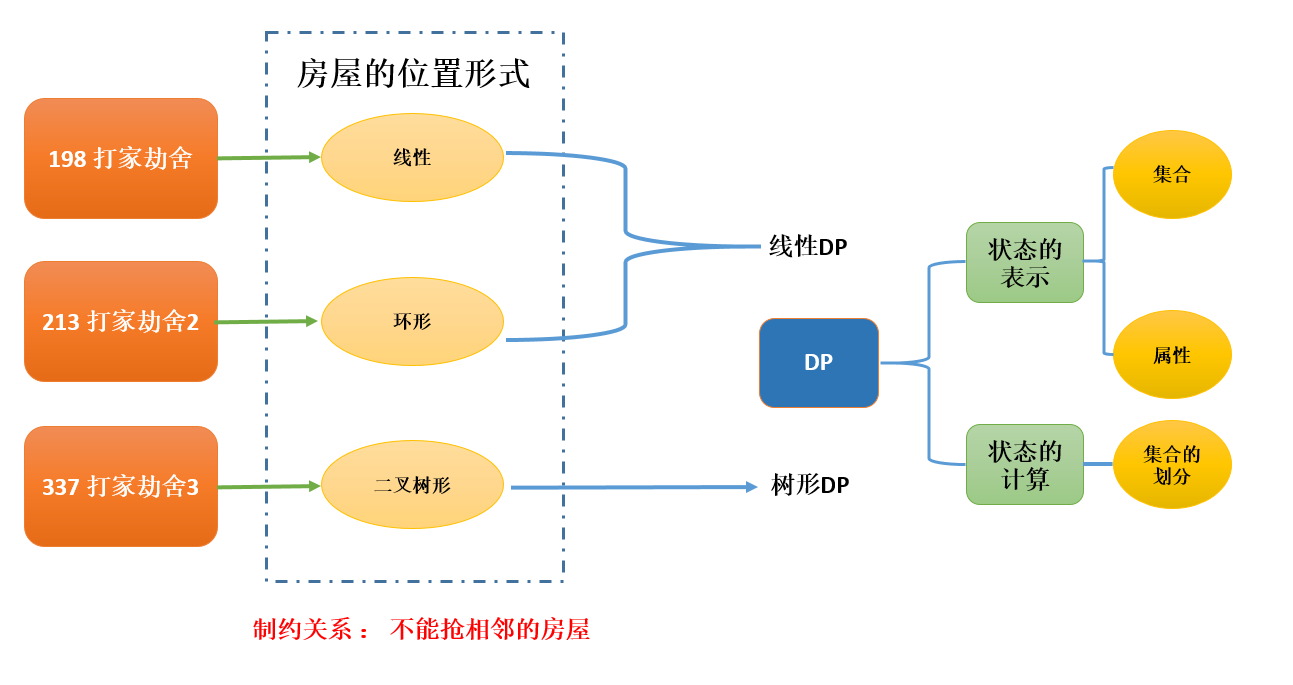
前言

leetcode上打家劫舍的问题根据房屋排列的位置形式不同，一共分为3种，分别线性，环形和二叉树形状。制约的条件为，不能抢相邻的房屋。

对于环形的排列的房屋，和线性的相比，体现在首尾两房屋的制约，具体为首抢了，则尾一定不能抢。

对于二叉树形的房屋，制约关系体现在父节点与左右孩子节点的制约，具体为父节点抢了，左右孩子一定不能抢。

三种的解法为动态规划，都是从头开始抢到了当前房屋，当前房屋抢还是不抢分情况讨论。

leetcode 198 打家劫舍

具体链接 198. 打家劫舍

思路 [线性dp]

• 状态表示

• 集合f(i) : 所有从头开始抢，抢到了i房屋的方案
• 属性 ： 最大值

• 状态计算

集合的划分

• 房屋i不抢 ： f(i) = f(i - 1)
• 房屋i抢 ： f(i) = f(i - 2) + nums[i]

代码

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(!n) return 0;
        if(n == 1) return nums[0];
        if(n == 2) return max(nums[0], nums[1]);

        vector<int> dp(n);
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);

        for(int i = 2; i < n; i++)
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]); // 这里抢 和 这里不抢

        return dp[n - 1];
    }
};

leetcode 213 打家劫舍II

链接 ：213. 打家劫舍 II

思路 [线性dp]

因为首尾房屋有着制约关系，所以分首房屋抢与不抢两种情况讨论，最后取较大值。

（1）首房屋抢

• 状态表示

• 集合f(i) : 所有从头开始抢，抢到了i房屋的方案
• 属性 ： 最大值

• 状态计算

集合的划分

• 房屋i不抢 f(i) = f(i - 1)
• 房屋i抢 f(i) = f(i - 2) + nums[i]
• 特殊情况 ： i为最后一个房屋时 f(i) = f(i - 1)

（2）首房屋不抢

• 状态表示

• 集合g(i) : 所有从头开始抢，抢到了i房屋的方案
• 属性 ： 最大值

• 状态计算

集合的划分

• 房屋i不抢 : g(i) = g(i - 1)
• 房屋i抢 : g(i) = g(i - 2) + nums[i]

代码

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(!n) return 0;
        if(n == 1) return nums[0];
        if(n == 2) return max(nums[0], nums[1]);

        vector<int> f(n), g(n);
        //第一个抢
        f[0] = f[1] = nums[0];
        //第一个不抢
        g[0] = 0, g[1] = nums[1];
        for(int i = 2; i < n; i++)
        {
            // 最后一个受到第一个抢的制约，所以特殊判断下
            if(i == n - 1)
                f[i] = f[i - 1];
            else
                f[i] = max(f[i - 1], f[i - 2] + nums[i] );
            g[i] = max(g[i - 1], g[i - 2] + nums[i]);
        }
        return max(f[n - 1], g[n - 1]);
    }
};

leetcode 337打家劫舍IIi

链接 ：337. 打家劫舍 III

思路 [树形dp]

• 状态表示

• 集合
  • f(i，0) 表示偷完以i为根的子树，且不对结点i进行偷窃的所有方案
  • f(i,1) : 表示偷完以i为根的子树，且对结点i进行偷窃的所有方案
• 属性 ： 最大值

• 状态计算

集合的划分

• f(i,0) ： 左右孩子没有限制，为了取得最大值，即让左右都取得最大值即可

即：f(i,0) = max(f(i->left,0), f(i->left,1))+ max(f(i->right,0), f(i-> right,1))

• f(i,1) ： 左右孩子的不能选 ,

即：f(i,1) = i-> val + f(i->left, 0) + f(i -> right, 0)

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode*, unordered_map<int, int>> f; 

    int rob(TreeNode* root) {
        dfs(root);
        return max(f[root][0], f[root][1]);
    }

    void dfs(TreeNode *root)
    {
        if(!root) return;
        dfs(root -> left);
        dfs(root -> right);
        // 若当前层进行了偷窃 那么下一层就不能偷窃 状态即为 0
        f[root][1] = root -> val + f[root -> left][0] + f[root -> right][0];
        // 若当前层未进行了偷窃 那么下一层可以偷窃， 
        f[root][0] = max(f[root -> left][0], f[root -> left][1]) + max(f[root -> right][0], f[root -> right][1]);
    }
};

拓展

AcWing 285. 没有上司的舞会

思路 [树形DP]

状态表示

• 集合
  • f(u, 0): 所有从以u为根的子树中选择，且不选u这个的方案
  • f(u, 1): 所有从以u为根的子树中选择，且选u这个的方案
• 属性
  • 最大值

状态计算

$f(u, 0) = sum (max(f(si, 0), f(si, 1)))$
$f(u, 1) = happy[u] + sum (f(si, 0))$

代码

建树： 图的存储 - 邻接矩阵

• 边的读入
• 在临接表中插入一条边

找根节点

 #include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 6010;

int n;
int happy[N];
int h[N], e[N], ne[N], idx;
int f[N][2];
bool has_fa[N]; // 判断有没有父节点，用来找根节点（由于题目没有告诉我们）

void add(int a, int b) // 在邻接表中插入一条边  头插法
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
    // 生成节点，修改节点指针，修改链表头节点指针
}

void dfs(int u )
{
    f[u][1] = happy[u];
    //枚举所有儿子
    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        dfs(j);

        f[u][0] += max(f[j][0], f[j][1]);
        f[u][1] += f[j][0];
    }

}
int main()
{

    scanf("%d", &n);

    for(int i = 1 ; i <=n; i ++) scanf("%d", &happy[i]); // 下标从1开始 里面是  <= 

    memset(h, -1, sizeof h);   //初始邻接表表头
    // 读入每一条边 共 n -1 条边
    for(int i = 0; i < n - 1; i ++)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(b, a); //b是a的父节点
        has_fa[a] = true;
    }

    // 找根节点
    int root = 1;
    while(has_fa[root]) root ++;

    dfs(root);

    printf("%d\n", max(f[root][0], f[root][1]));

    return 0;
}