函数定义

函数是将一个对象转化为另一个对象的规则（函数是规则）。起始对象称为输入，来自定义域的集合。返回对象称为输出，来自上域的集合。
- $f(x)=x^2，这样定义了一个函数f。f是一个变换规则，而f(x)是吧这个变换规则应用于变量x后得到的结果。因此说f(x)是一个函数是不正确的，应该说f是一个函数$
- 值域是上域的一个子集。上域是可能输出的集合，值域是实际输出的集合
- 不同定义域表示不同的函数

区间表示法

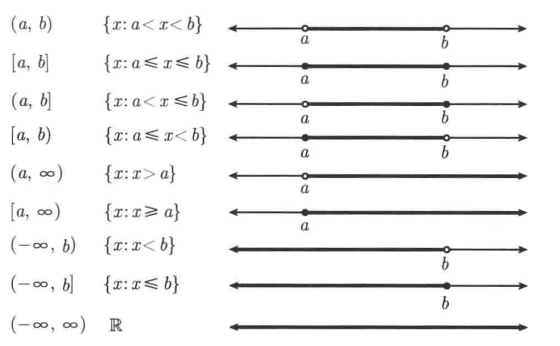
[a,b]是指从a到b端点间的所有实数，包括a和b。像[a.b]这种形式表示的区间我们称作闭区间。(a,b)指介于a和b之间但不包括a和b真的所有实数的集合。像(a,b)这种形式表示的区间称作开区间。

求定义域

• 分数的分母不能为0
• 不能取一个负数的平方根
• 不能取一个负数或零的对数

求$f(x)=\frac{log_{10}(x+8)\sqrt{26-2x}}{(x-2)(x+19)}$的定义域
1. 取（26-2x）的平方根，这个量必须是非负的。即26-2x>=0。即x<=13
2. 取(x+8)的对数，这个量必须是正的。即x+8>0。得x>-8。到目前为止该函数的定义域是(-8,13]
3. 分母不能为0，也就是说(x-2)!=0且(x+19)1=0。即x!=2且x!=19。x!=19已在定义范围外了，所以最终定义域是(-8,19){2}，这里反斜杠表示“不包括”

垂线检验

如果你有某个图像并想知道它是否是函数的图像，你就看看是否任何的垂线和图像相交多于一次．如果是这样的话，那它就不是函数的图像，反之，如果没有一条垂线和图像相交多于一次，那么你的确面对的是函数的图像。

反函数

给定一个实数Y,那么在J定义域中的哪个x满足f(x) = y? 首先要注意的是，y必须在J的值域中否则，根据定义，将不再有x的值使得f(x) = y成立了如此在J定义域中将没有这样的x满足f(x) = Y, 因为值域是所有的可能输出

1. 从一个函数f出发，使得对于在f值域中的任意y,都只有唯一的x值满足f (x) =y。也就是说不同的输入对应不同的输出。现在，我们就来定义反函数$f^{-1}$
2. $f^{-1}$的定义域和f的值域相同
3. $f^{-1}$的值域和f的定义域相同
4. $f^{-1}$的值就是满足f(x)= y的x。

水平线校验

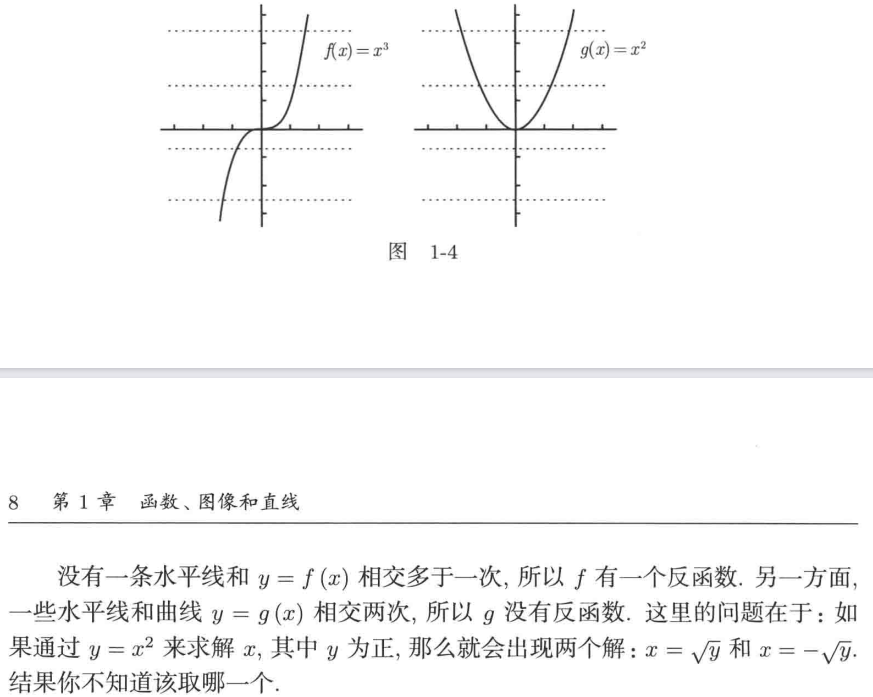
如果每一条水平线和一个函数的图像相交至多一次，那么这个函数就有一个反函数。如果即使只有一条水平线和图像相交多于一次，那么这个函数就没有反函数

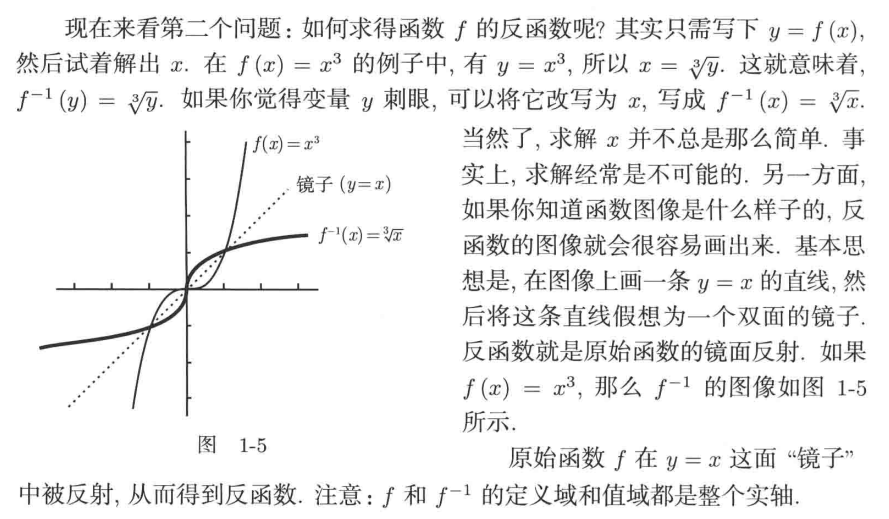
求反函数

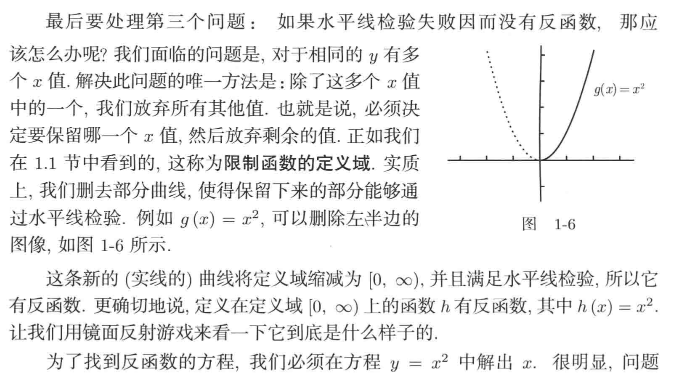
限制定义域

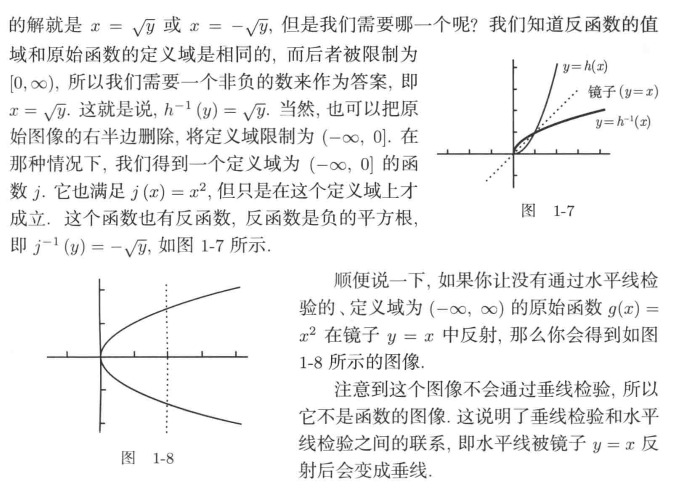
反函数的反函数