二叉树的定义

• 二叉树是n(n>=0)个结点的有限集合
• 每个结点至多只有2棵子树
• 二叉树是有序数，其左右子树不能颠倒，否则称为另一个二叉树

二叉树与度为2的树的区别

• 度为2的树至少有3个结点，而二叉树可以为空
• 度为2的有序树的孩子的左右次序是相对于另一孩子而言的，若某个结点只有一个孩子，则这个孩子无须区分左右次序。二叉树无论其孩子数是否位2，均需确定其左右次序，即二叉树的结点的次序不是相对另一次序而言的，而是确定的。

几个特殊的二叉树

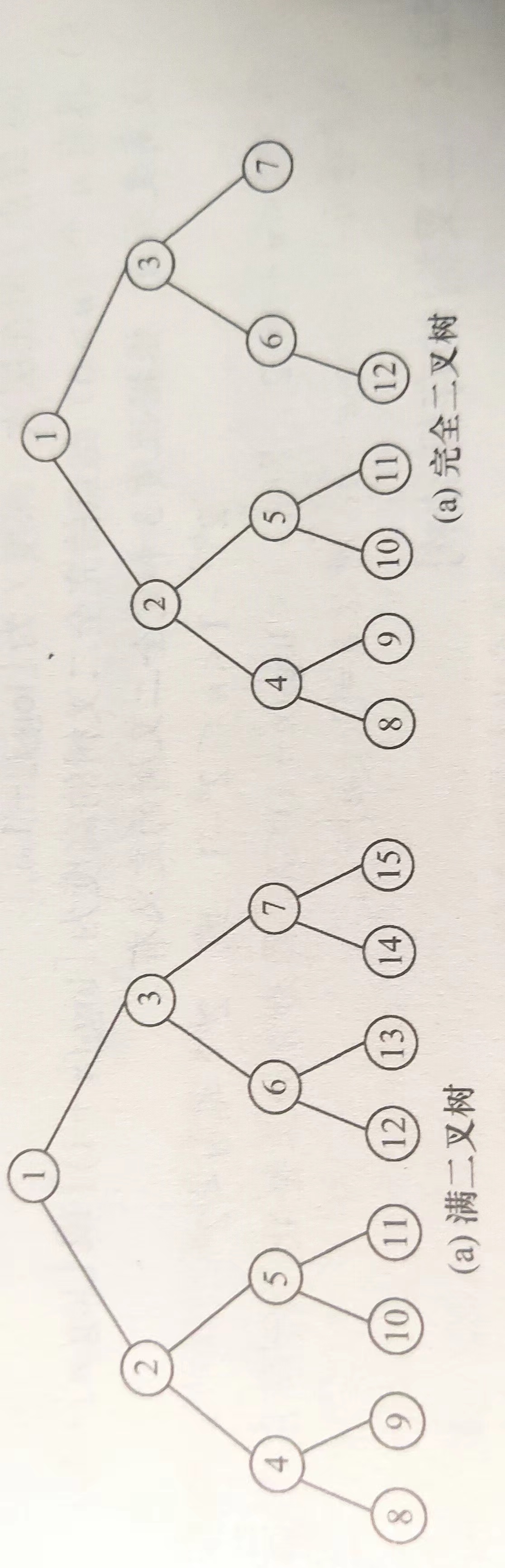
满二叉树

一棵高度为h，含有$2^h-1$（$n=\frac{m^h-1}{m-1}=\frac{2^h-1}{2-1}=2^h-1$）个结点的二叉树称为满二叉树。即树的每层都含有最多的结点，且除叶节点之外每个结点的度都为2。对树的结点从上到下，从左到右从1开始编号，对于编号为i的结点，其双亲为$\lfloor i/2 \rfloor$，左孩子为$2i$，右孩子为$2i+1$

完全二叉树

高度为h,有n个结点的二叉树，当且仅当其每个结点都与其高度为h的满二叉树中编号为1~n的结点一一对应时，称为完全二叉树

• 若$i <= \lfloor n/2 \rfloor$，则结点i为分支节点，否则为叶结点
• 叶节点只可能在层次最大的两层出现，以此排列在该层的最左边位置上
• 有且只有一个度为1的结点，而且该节点只有左孩子无右孩子
• 若编号为i的结点为叶节点或只有左孩子，则编号大于i的结点均为叶节点
• 若n为奇数，则每个分支都有左孩子和右孩子。若n为偶数，编号最大的结点(n/2)只有左孩子，其余都有左孩子和右孩子

二叉排序树

左子树上所有节点的关键值均小于根节点的关键值；右子树上所有节点的关键值均大于根节点的关键值；左子树和右子树各是一棵二叉排序树。

平衡二叉树

树上任意一个节点的左子树和右子树深度之差不超过1

二叉树的性质

• 非空二叉树上的叶节点数等于度为2的结点数+1.即$n_0=n_2+1$。n为二叉树的总结点数，则$n=n_0+n_1+n_2=分支数+1=0n_0+1n_1+2n_2+1$，可以得到$n1=n-0n_0-2n_2-1=n-2n_2-1$，代入得$n=n_0+(n-2n_2-1)+n_2=n_0+n-n_2-1$，移项得$n_0=n_2+1$
• 非空二叉树上第K层至多有$2^{k-1}$个结点（k>=1）
• 高度为h的二叉数最多有$2^h-1$个结点（h>=1）
• 当i>1时。节点i的双亲的编号是$\lfloor i/2 \rfloor$。即当i为偶数时，其双亲编号为$i/2$，他是双亲的左孩子；当i为奇数时，其双亲编号为$(i-1)/2$，他是双亲的右孩子。
• 当2i<=n时，节点i的左孩子为2i，否则无左孩子
• 当2i+1<=n时，结点i的右孩子为2i+1，否则无右孩子
• 节点i所在层次（深度）为$\lfloor log_2i \rfloor+1$
• n个结点的完全二叉树的高度为$\lceil log_2(n+1) \rceil$。$2^{h-1}-1<n<=2^h-1$，得$2^{h-1}<n+1<=2^h$，即$h-1<log_2(n+1)<=h$
• 在含有n个结点的二叉链表中，含有n+1个空链域。n个结点可以有2n条边（左指针和右指针），而二叉链表只需用到其中n-1条边，剩下n+1条边没用

常用的公式

• $n_0=n_2+1$
• $n=n_0+n_1+n_2=n_1+2n_2+1$(在完全二叉树中，n1等于0或1)
• n=分支数+1

需注意的题

1.一棵完全二叉树有1001个结点，其中叶节点的个数是？
答案是501。$n=n_0+n_1+n_2=n_1+2n_2+1$，其中$n_1$为0或1；若$n_1$为0，则$n=1001=2n_2+1$，得$n_2=500，n_0=n_2+1=501$；若$n_1为1，则n=1001=1+2n_2+1$，$999$不能整除2，所以$n_1$只能为0

2.若一棵二叉树有126个结点，在第7层至多有多少个结点？
答案是63。7层满二叉树至多有$2^7-1=127$个节点,但现在只有126个结点，问题问的是至多，则第6层及以前是满二叉树，只能是第7层有度为1的结点，即$2^{7-1}-1=63$

3.对于任意一棵高度为5且有10个结点的二叉树，若采用顺序结构存储结构保存，每个结点至少占1个存储单元（仅存放结点的数据信息），则存放该二叉树需要的存储单元数量至少是？
答案是31。高度为5的满二叉树$2^5-1=31$，可以保证该存储单元存储任意高度为5的二叉树

4.一个具有1025个结点的二叉树的高h为？
答案是11~1025,。最小高度是完全二叉树=$\lfloor log_2(1025) \rfloor+1=11$，最大是每个结点为1层，即1025

5.已知一棵二叉树按顺序存储结构进行存储，设计一个算法，求编号分别为i和j的两个节点的最近公共祖先的结点的值。

//二叉树的最近公共祖先，不是多叉树的最近公共祖先
const int N = 110;
//p是存储树的数组
int p[N];
int lca(int i, int j){
    while(i != j) {
        //找i的根节点
        if(i > j) i /= 2;
        //找j的根节点
        else j /= 2;
    }
    return p[i];
}

二叉树的遍历

由二叉树的递归定义可知。遍历一棵二叉树要决定对根节点N，左子树L和右子树R的访问顺序。常见的遍历次序有先序（NLR），中序（LNR）和后序（LRN），其中序是指根节点在何时被访问，

先序遍历NLR

//递归
void nlr(Node u){
    if(u == null) return;
    System.out.println(u.val);
    nlr(u.left);
    nlr(u.right);
}
//非递归
void nlr(Node u){
    LinkedList<Node> stk = new LinkedList<>();
    while(u != null || !stk.isEmpty()){
       if (u != null){
           System.out.println(u.val);
           stk.add(u);
           u = u.left;
       }else {
           u = stk.pollLast();
           u = u. right;
       }
    }
}

中序遍历

//递归
void lnr(Node u){
    if(u == null) return;
    nlr(u.left);
    System.out.println(u.val);
    nlr(u.right);
}

//非递归
void lnr(Node u){
    LinkedList<Node> stk = new LinkedList<>();
    while(u != null || !stk.isEmpty()){
        if (u != null) {
            stk.add(u);
            u = u.left;
        }else {
            u = stk.pollLast();
            System.out.println(u.val);
            u = u.right;
        }
    }
}

后序遍历

//递归
void lrn(Node u){
    if(u == null) return;
    nlr(u.left);
    nlr(u.right);
    System.out.println(u.val);
}
//非递归
lrn(Node u){
    LinkedList<Node> stk = new LinkedList<>();
    Node r = null;
    while(u != null || !stk.isEmpty()){
       if (u != null){
           stk.add(u);
           u = u.left;
       }else {
           u = stk.peekLast();
           if (u.right != null && u.right != r) {
               u = u.right;
           }else {
               u = stk.pollLast();
               System.out.println(u.val);
               r = u;
               u = null;
           }
       }
    }
}

层序遍历（bfs）遍历二叉树

void bfs(Node u){
    LinkedList<Node> queue = new LinkedList<>();
    queue.add(u);
    while (!queue.isEmpty()) {
        Node p = queue.pollFirst();
        System.out.println(p.val);
        if (p.left != null) queue.add(p.left);
        if (p.right != null) queue.add(p.right);
    }
}

遍历序确定一棵二叉树

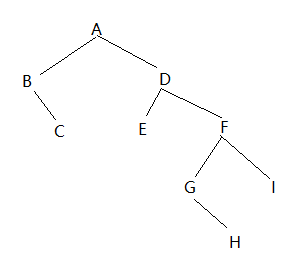
先序序列和中序序列

求先序$ABCDEFGHI$和中序$BCAEDGHFI$所确定的二叉树
总体思想是用中序序列划分先序序列
1. 先从先序看，A是第一个遍历到的，说明A是整棵树的根节点；
2. 在中序找A的位置，在A的左边BC是A的左子树，在A的右边DEFGHI是A的右子树
3. 先看A的左子树BC，BC是先序序列，所以B是C的父结点
4. 在中序找B的位置，发现B的左边没有，说明B没有左子树；B的右边有C，说明B的右子树是C；
5. 再看A的右子树DEFGHI
6. 在中序找D的位置，D的左边是E，E是D的左子树;D的右边是FGHI，FGHI是D的右子树；
7. 以此类推

中序序列和后序序列

求中序$BCAEDGHFI$和后序$CBEHGIFDA$所确定的二叉树
总体思想是用中序序列划分后序序列
1. 先从后序看，倒数第一个元素A是整棵树的根结点
2. 在中序找A的位置，在A的左边CB是A的左子树，在A的右边EHGIFD是A的右子树
3. 先看A的左子树CB，CB是后序序列，所以B是C的父结点
4. 在中序找B的位置，发现B的左边没有，说明B没有左子树；B的右边有C，说明B的右子树是C；
5. 再看A的右子树EHGIFD，EHGIFD是后序序列，D是EHGIF的父节点
6. 在中序找D的位置，D的左边是E，E是D的左子树;D的右边是HGIF，HGIF是D的右子树；
7. 以此类推

层序序列和中序序列

求层序$ABDCEFGIH$和中序$BCAEDGHFI$所确定的二叉树
总体思想是用中序序列划分层序序列
1. 先划分层序序列，A为第一层，是树的根结点
2. 在中序中找A，A的左边是BC是A的左子树，右边是EDGHFIA的右子树
3. 先看A的左子树BC，现在不能确定BC哪个是父结点
4. 回看层序，A的下一个是B，说明B是A的左子树。那C是B的左子树还是右子树？
5. 回看中序，C在B的右边，所以C是B的右子树
6. A的右子树EDGHFIA，不知道哪个是父节点
7. 回看层序，第二层只能有2个结点，一个是B另一个是D，现在只能是D为父结点
8. 在中序里，E在D的左边为D的左子树，GHFI在D的右边为右子树
9. GHFI哪个是父节点？
10. 第三层有4个结点，分别为B的左子树空，B的右子树C，D的左子树E
11. 那么剩下的节点只能是在层序中紧跟着E的F，所以F为父结点
12. 中序中F的左边是GH为F的左子树，右边是I为F的右子树
13. GH中哪个是父结点？
14. 在层序中，紧接着F的是G，紧着G的是I，那么G为H父结点
15. 最后这个H在G的右边，所以为G的右子树

线索二叉树

传统的二叉链表仅能体现一种父子关系，不能直接得到结点在遍历的前驱和后继。在含有n个结点的二叉树中，右n+1个空指针。由此设想能否利用这些空指针来存放其前驱或后继的指针？引入线索二叉树正是为了加快查找节点的前驱和后继的速度，

规定：若无左子树，令其左子节点指向其前驱结点；若无后子树，令其右子结点指向其后继结点。现在一个结点有5个标识指针域，如下所示。

其tag含义如下：
- ltag=0，left指向结点的左孩子
- ltag=1，left指向结点的前驱
- rtag=0，right指向结点的右孩子
- rtag=1，right指向结点的后继

中序线索二叉树

找前驱。如果ltag=1，直接找到前驱，如果LTag=0，则走到该结点左子树的最右边的结点，即为要寻找的结点的前驱。
找后继。rtag=1，直接找到后继，如果rtag=0，则走到该结点右子树的最左边的结点，即为要寻找的结点的后继。

先序线索二叉树

后序线索二叉树