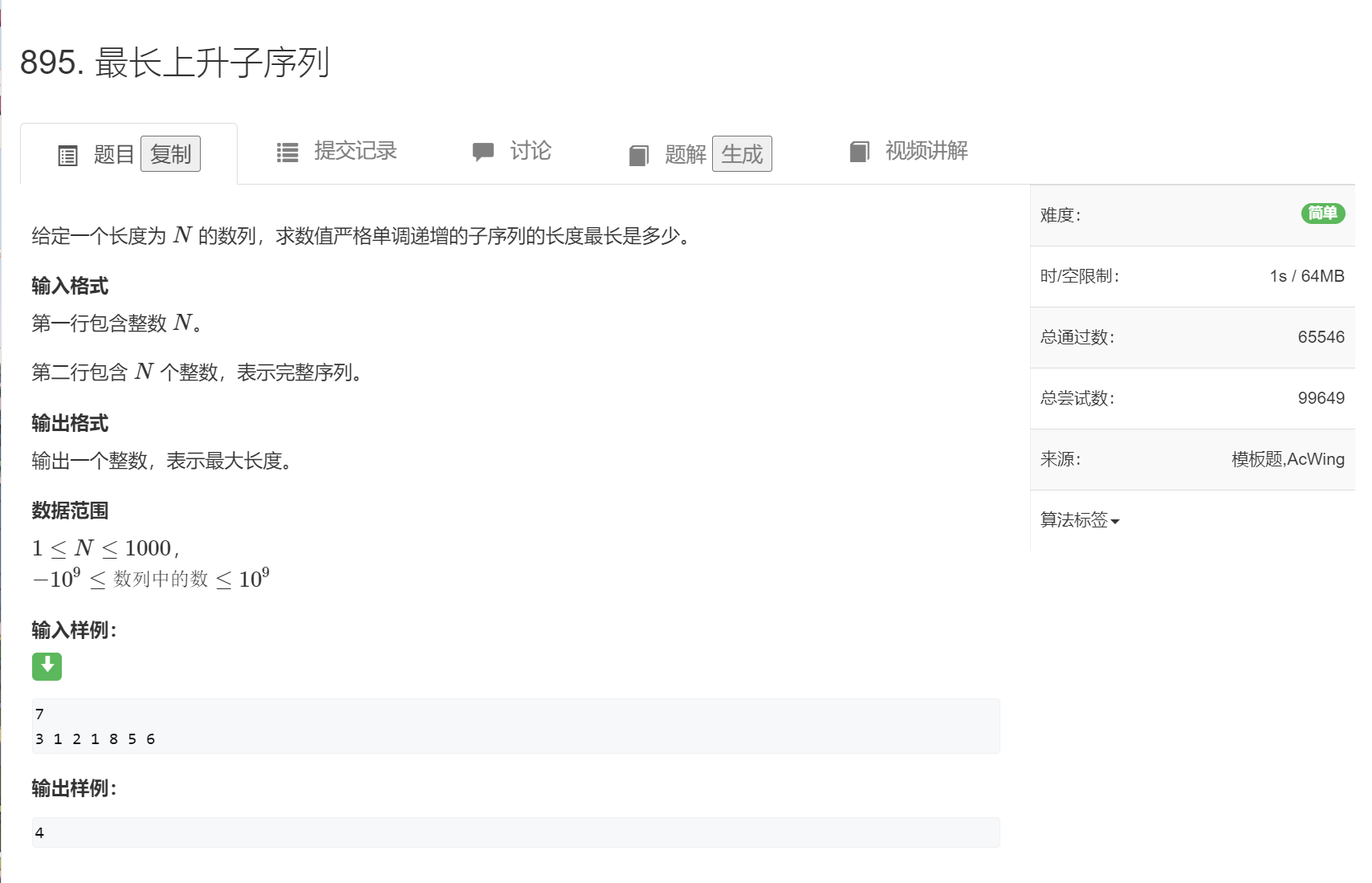
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1010;
int f[N],n,a[N];
int main()
{
    scanf("%d",&n);

    for(int i=1;i<=n;i++)
    scanf("%d",&a[i]);

    for(int i=1;i<=n;i++)
    {
        f[i] = 1;
        for(int j=1;j<n;j++)
        {
            if(a[j]<a[i])
            f[i] = max(f[i],f[j]+1);
        }
    }
    int res=0;
    for(int i=1;i<=n;i++)
     res = max(res,f[i]);

     cout<<res<<endl;

    return 0;
}

q[N]是严格单格单调递增的，可以用二分(使用二分需要严格单调的条件)

q数组的含义:q数组存储所有不同长度的上升子序列的结尾是最小值的数

解释一下为什么q数组是严格单调递增的？

举个例子：如果第q[6]<q[5]的话，那么组成q[6]的第五个数一定也是小于q[5]的，并且这五个数(q[6]的前五个数)也可以组成一个新的q[5]，并且这个q[5]结尾的值还要比原来这个q[5]的结尾的值还要小(q[6]是上升子序列，且q[6]比q[5]小)，又因为q数组的含义是存储上升子序列的结尾是最小值的数，可以看出这是矛盾的，故q数组是一个单调递增的数组，可以使用二分。

// 贪心思想

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N =100010;

int n; 
int a[N];  //存储序列
int q[N]; //存储所有不同长度的上升子序列结尾的最小值

int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);

    int len = 0; //q中的元素个数
    //q[0] = -2e9;  //-2e9小于所有数,可以保证小于某个数最大数一定存在

    for(int i=0;i<n;i++)
    {
        int l=0,r = len;
        while(l<r) //每次二分找小于a[i]的最大的数,便可以找到这个数的序列的长度,可以用这
        {          //个长度去更新len
            int mid =l+r+1 >>1;
            if(q[mid] < a[i]) l = mid;
            else r = mid-1;
        }

        len = max(len,l+1); //存储最大长度
        q[r+1] = a[i]; //(r是小于a[i]的最大的数,q[r+1]>=a[i]的,为使得r+1变小一些)
    }


    printf("%d\n",len);

    return 0;
}