一点人生经验：
数论中一些难题需要掌握数学证明后，在数学证明中挖掘信息

欧拉函数：求互质数的个数
用公式分别求数组中每个数的欧拉函数：
1. 先因式分解
2. 套公式

证明：增增减减所有（n）个质因子的倍数

瓶颈在分解质因数：O(sqrtn)

**一次性用O(n)复杂度求1 - n中每个数的欧拉函数：**
借鉴线性筛法
note：
    （1）phi(质数) = 质数 - 1
    （2）i mod j == 0：phi(primes[j] * i) = primes[j] * phi(i);
            公式里phi只与底数有关，无关次数
            j为i的其中一个质因子，因此phi(i)里已求得(1-1/primes[j])
    （3）i mod j != 0：
            说明此时的primes[j]为primes[j]*i的最小质因子，且不是i的质因子
            因此phi(primes[j] * i) = primes[j] * phi[i] * (1 - 1 / primes[j])

            大佬解释i mod j != o的pj含义
            https://www.acwing.com/activity/content/code/content/5374176/

欧拉函数用途：欧拉定理
    若n, a为正整数，且n，a互质，则: a^φ(n)≡1(mod n)
    费马小定理：
        p为质数，a^(p-1) ≡ 1 mod p

快速幂: 在O(logk)时间复杂度下算a^k % p （a, k, p均在1-1e9之间)
核心思路：反复平方法
用递推的方式求出所有a^(2^i)
再将k从10进制转为2进制，将二进制为1的数带入求得结果

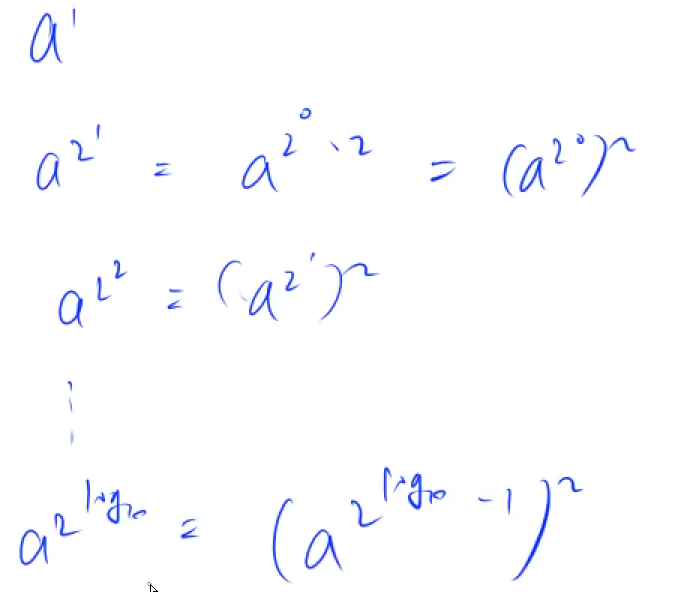
扩展欧几里得算法：
补充：
裴蜀定理：
整数a、b和它们的最大公约数c，一定存在整数x,y，使ax+by=c成立，若d是c的倍数，显然也一定存在整数x,y，使得 ax+by=d成立

有解充要条件：d为(a, b)倍数

中国剩余定理：

https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%9B%BD%E5%89%A9%E4%BD%99%E5%AE%9A%E7%90%86

https://www.acwing.com/file_system/file/content/whole/index/content/4808/
02：25： 解释题目和中国剩余定理
    09:03 限制条件
12:43 - 21:27 证明推导

同余知识补充
https://zhuanlan.zhihu.com/p/401243582