题目来源于《挑战程序设计竞赛》,题目涉及的算法只对应相关章节 (不一定是最优解的,思路写的有点简陋)
例题1 Sequence 传送门
题意:
给定N个数字组成的序列,保证A1比其他数字都大。先要将这个序列分成三段,并将每段分别反转,求能得到的字典序最小的序列的什么?要求每段都不为空。
思路:
首先,确定第一段的位置。题中限制𝐴_1大于其他任何数字,那么确定第一段的分割位置只需考虑第一段就足够了。只需将数组A反转,求一遍后缀数组,答案为满足条件的字典序最小的方案。(注意限制每段不能为空)
然后,将剩余部分分割成两段,由于没有第一段的条件约束,这两段要综合考虑。将序列分割成两段再分别反转得到的序列,可以看作是将两个原序列拼接得到的新序列中的某个子串反转得到的序列。
例如:原串 S=ABCDEFGH
以D右侧为分割线,将原串分割成 S1=ABCD, S2=EFGH,反转S1、S2拼接后为DCBAHGFE
令 T = S + S,即 T=ABCDEFGHABCDEFGH,标黑处子串的反转后为上述串
因此,可以将剩余部分扩倍,反转后,求一遍后缀数组,即可得到答案。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 4e5 + 10;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(int s[], int n, int m)
{
int i, p, w;
memset(cnt, 0, sizeof cnt);
//for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
memset(cnt, 0, sizeof(cnt));
//for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
memcpy(oldrk, rk, sizeof(rk));
//for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
int n, s[N], val[N], tmp1[N], tmp2[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i++) scanf("%d", &s[i]);
vector<int>v;
for (int i = 1; i <= n; i++) v.push_back(s[i]);
stable_sort(v.begin(), v.end());
v.erase(unique(v.begin(), v.end()), v.end());
int len = v.size();
for (int i = 1; i <= n; i++)
val[i] = lower_bound(v.begin(), v.end(), s[i]) - v.begin() + 1;
reverse(val + 1, val + n + 1);
reverse(s + 1, s + n + 1);
get_sa(val, n, len);
vector<int>ans;
//取第一段
int p = 0;
for (int i = 1; i <= n; i++)
if (sa[i] > 2)
{
p = sa[i];
break;
}
for (int i = p; i <= n; i++) ans.push_back(s[i]);
reverse(val + 1, val + n + 1);
reverse(s + 1, s + n + 1);
//取第二、三段
int tot = 0;
for (int i = n - p + 2; i <= n; i++)
tmp1[++tot] = s[i], tmp2[tot] = val[i];
int cnt = tot;
for (int i = 1; i <= cnt; i++)
tmp1[++tot] = tmp1[i], tmp2[tot] = tmp2[i];
reverse(tmp1 + 1, tmp1 + tot + 1);
reverse(tmp2 + 1, tmp2 + tot + 1);
get_sa(tmp2, tot, len);
for (int i = 1; i <= tot; i++)
if (sa[i] <= tot / 2 && sa[i] > 1)
{
p = sa[i];
break;
}
for (int i = p, j = 1; j <= tot / 2; i++, j++)
ans.push_back(tmp1[i]);
for (int i = 0; i < ans.size(); i++) printf("%d\n", ans[i]);
return 0;
}
例题2 Secretary 传送门
题意:
给定两个字符串S和T。请计算两个字符串最长的公共字符串子串的长度。
思路:
首先,考虑一个简化的问题,计算一个字符串中至少出现两次的最长子串。答案一定会在后缀数组中相邻两个后缀的公共前缀之中,所以只要考虑它们就好了。这是因为子串的开始位置在后缀数组中相距越远,其公共前缀的长度也就越短。因此,高度数组的最大值其实就是答案。
再考虑原问题的解法。因为对于两个字符串,不好直接运用后缀数组,因此我们可以将S和T,通过在中间插入一个不会出现的字符(’#’)拼成一个新串P。之后计算方法和上述相同。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e4 + 10;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
// px[i] = rk[id[i]](用于排序的数组所以叫 px)
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(char s[], int n)
{
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int T, n, m;
char s[N], t[N];
int main()
{
scanf("%d", &T);
getchar();
while (T--)
{
cin.getline(s + 1, N);
cin.getline(t + 1, N);
n = strlen(s + 1);
m = strlen(t + 1);
s[n + 1] = '#';
strcpy(s + n + 2, t + 1);
get_sa(s, n + m + 1);
get_height(s, n + m + 1);
int ma = 0;
for (int i = 2; i <= n + m + 1; i++)
{
int pos1 = sa[i - 1], pos2 = sa[i];
if ((pos1 <= n && pos2 <= n) ||
(pos1 >= n + 2 && pos2 >= n + 2))
continue;
ma = max(ma, ht[i]);
}
printf("Nejdelsi spolecny retezec ma delku %d.\n", ma);
}
return 0;
}
例题3 最长回文子串 传送门
题意:
输入一个字符串Str,输出Str里最长回文子串的长度。
思路:
与例题2类似,令 S 的反串为 T
将原串 S 和 T 利用间隔符 ’#’ 拼接起来
对奇偶两种情况分类讨论,求对应位置的lcp,将其转化为回文串长度,取最大值。
注意两侧的边界。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 220050;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
// px[i] = rk[id[i]](用于排序的数组所以叫 px)
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(char s[], int n)
{
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int Log[N], f[N][23];
void RMQ_pre(int n)
{
Log[0] = -1;
for (int i = 1; i <= n; i++)
{
if (!(i & (i - 1))) Log[i] = Log[i - 1] + 1;
else Log[i] = Log[i - 1];
f[i][0] = ht[i];
}
for (int j = 1; (1 << j) <= n; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
int RMQ_min(int l, int r)
{
int d = Log[r - l + 1];
return min(f[l][d], f[r - (1 << d) + 1][d]);
}
char s[N], t[N];
int main()
{
while (~scanf("%s", s + 1))
{
int tot = 0, n = strlen(s + 1);
for (int i = 1; i <= n; i++) t[++tot] = s[i];
t[++tot] = '#';
for (int i = n; i >= 1; i--) t[++tot] = s[i];
get_sa(t, tot);
get_height(t, tot);
RMQ_pre(tot);
int ma = 0;
for (int i = 1; i <= n; i++)
{
int x = i, y = n * 2 + 2 - i;
//奇数长度
int rkx = rk[x], rky = rk[y];
if (rkx > rky) swap(rkx, rky);
ma = max(ma, RMQ_min(rkx + 1, rky) * 2 - 1);
//偶数长度
if (i == 1) continue;
x = i; y = n * 2 + 3 - i;
rkx = rk[x], rky = rk[y];
if (rkx > rky) swap(rkx, rky);
ma = max(ma, RMQ_min(rkx + 1, rky) * 2);
}
printf("%d\n", ma);
}
return 0;
}
习题1 Glass Beads 传送门
题意:
求所给字符串同构的字典序最小的字符串的起始位置。
思路:
令原字符串为S, len = |S|, 构造字符串T = S + ‘}’ + S
求一遍后缀数组,取满足sa[i] <= len的最小的sa[i]
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e4 + 10;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
int t;
char s[N];
int main()
{
scanf("%d", &t);
while (t--)
{
scanf("%s", s + 1);
int n = strlen(s + 1);
for (int i = 1; i <= n; i++) s[n + i] = s[i];
s[n * 2 + 1] = '{';
get_sa(s, n * 2 + 1);
int ans = 0;
for (int i = 1; i <= 2 * n; i++)
{
if (sa[i] <= n)
{
ans = sa[i];
break;
}
}
printf("%d\n", ans);
}
return 0;
}
习题2 Common Substrings 传送门
题意:
求两个串长度大于等于k的公共子串的个数。
思路:
后缀数组+单调栈+差分
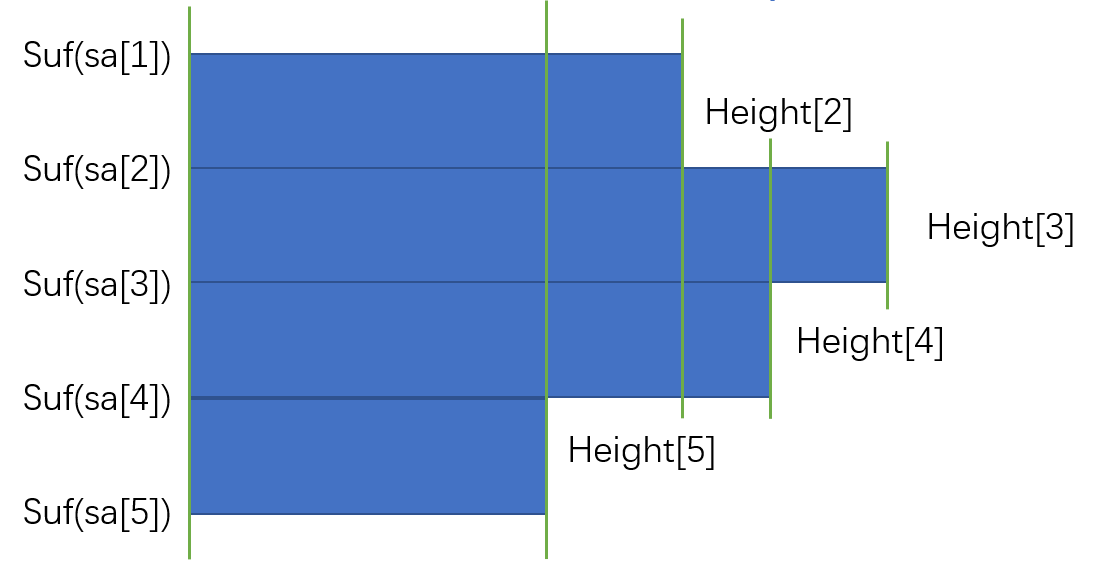
对于每两条相邻的绿线,作为一个整体计算,设当前计算横向区间为[l,r], 纵向区间为[L,R], cnt1为属于第一个串的个数,cnt2为属于第二个串的个数,那么对[l, r]所有点的贡献均为cnt1 * cnt2, 可用差分数组维护。
L = 左侧最近比height[i]小的下标 + 1, R = 右侧最近比height[i]小的下标 + 1, 可用单调栈维护
直接求大于k的也可以,此方法可求所有长度的解
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 2e5 + 10;
typedef long long ll;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(char s[], int n)
{
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int l[N], r[N], qu[N], tot;
void get_array_lr(int n)
{
ht[0] = ht[n + 1] = -1;
tot = 0; qu[++tot] = 0;
for (int i = 1; i <= n; i++)
{
while (tot && ht[i] <= ht[qu[tot]]) tot--;
l[i] = qu[tot] + 1;
qu[++tot] = i;
}
tot = 0; qu[++tot] = n + 1;
for (int i = n; i >= 1; i--)
{
while (tot && ht[i] <= ht[qu[tot]]) tot--;
r[i] = qu[tot] - 1;
qu[++tot] = i;
}
ht[0] = ht[n + 1] = 0;
}
int k;
char s[N], t[N];
vector<int>v[N];
ll sum[N];
int main()
{
while (~scanf("%d", &k) && k)
{
scanf("%s", s + 1);
scanf("%s", t + 1);
int lens = strlen(s + 1);
int lent = strlen(t + 1);
s[lens + 1] = '#';
for (int i = 1; i <= lent; i++) s[lens + 1 + i] = t[i];
int n = lens + lent + 1;
get_sa(s, n);
get_height(s, n);
get_array_lr(n);
for (int i = 1; i <= n; i++) v[i].clear();
for (int i = 1; i <= n; i++) v[ht[i]].push_back(i);
for (int i = 0; i <= n; i++) cnt[i] = 0;
for (int i = 1; i <= n; i++)
{
if (sa[i] <= lens) cnt[i] = 1;
else cnt[i] = 0;
cnt[i] += cnt[i - 1];
}
for (int i = 0; i <= n + 1; i++) sum[i] = 0;
for (int i = n; i >= 1; i--)
{
int rborder = 0;
for (int j = 0; j < v[i].size(); j++)
{
if (r[v[i][j]] <= rborder) continue;
rborder = r[v[i][j]];
int le = l[v[i][j]] - 1, ri = r[v[i][j]];
int cnt1 = cnt[ri] - cnt[le - 1];
int cnt2 = ri - le + 1 - cnt1;
ll val = 1LL * cnt1 * cnt2;
int mi = max(ht[le], ht[ri + 1]) + 1;
sum[mi] += val; sum[i + 1] -=val;
}
}
for (int i = 1; i <= n; i++) sum[i] += sum[i - 1];
for (int i = n; i >= 1; i--) sum[i] += sum[i + 1];
printf("%lld\n", sum[k]);
}
return 0;
}
习题3 Facer’s string 传送门
题意:
给你a、b串,让你求a串中有多少后缀与b串的所有后缀的公共前缀的长度最大值等于k。
思路:
恰好等于k的方案数可以转化为 大于等于k+1的方案数S1 减去 大于等于k的方案数S2
将a、b串用一个间隔符(此题可采用较大的数)拼起来,求一遍后缀数组,求得S1、S2, 两者作差即为答案
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(int s[], int n, int m)
{
int i, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(int s[], int n)
{
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int pre[N];
int cal_least_k(int n, int k)
{
int l = 0, r = 0, ans = 0;
for (int i = 1; i <= n; i++)
{
if (ht[i] < k)
{
if (l != 0 && pre[r] - pre[l - 1] != r - l + 1) ans += pre[r] - pre[l - 1];
l = r = 0;
continue;
}
if (l == 0) l = i - 1;
r = i;
}
if (l != 0 && r != 0) ans += pre[r] - pre[l - 1];
return ans;
}
int n, m, k;
int a[N], b[N];
int main()
{
while (~scanf("%d %d %d", &n, &m, &k))
{
for (int i = 1; i <= n; i++) scanf("%d", &a[i]), a[i]++;
for (int i = 1; i <= m; i++) scanf("%d", &b[i]), b[i]++;
a[n + 1] = 10005;
for (int i = 1; i <= m; i++) a[n + 1 + i] = b[i];
int tot = n + m + 1;
get_sa(a, tot, 10005);
get_height(a, tot);
for (int i = 0; i <= tot; i++) pre[i] = 0;
for (int i = 1; i <= tot; i++)
{
if (sa[i] <= n) pre[i] = 1;
pre[i] += pre[i - 1];
}
int ans = cal_least_k(tot, k) - cal_least_k(tot, k + 1);
printf("%d\n", ans);
}
return 0;
}
习题4 Common Palindromes 传送门
题意:
给定两个字符串S,T,询问(i,j,k,l)这样的四元组个数
满足S[i,j],T[k,l]都是回文串并且S[i,j]=T[k,l]
思路:
先预处理出后缀数组、高度数组和回文半径数组。
在每遇到一个长clen公共子串c的过程中,都遍历长度plen大于clen的公共回文子串p,将p的个数加到区间[clen, plen]中的每一个元素上去(因为两个字符串的lcp最大为clen,之前大于clen的公共回文子串无法传递)。
每出现一次长plen的公共回文子串p,都代表出现了一次plen-1,plen-2, …clen的公共回文子串,此过程可用树状数组维护。
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef map<int, ll>::iterator IT;
const int N = 4e5 + 50;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(char s[], int n)
{
for (int i = 0; i <= n; i++) ht[i] = 0;
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int Log[N], f[N][21];
void RMQ_pre(int n)
{
Log[0] = -1;
for (int i = 1; i <= n; i++)
{
if (!(i & (i - 1))) Log[i] = Log[i - 1] + 1;
else Log[i] = Log[i - 1];
f[i][0] = ht[i];
}
for (int j = 1; (1 << j) <= n; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
f[i][j] = min(f[i][j - 1], f[i + (1 << j - 1)][j - 1]);
}
int RMQ_min(int l, int r)
{
int d = Log[r - l + 1];
return min(f[l][d], f[r - (1 << d) + 1][d]);
}
char s[N], t[N], p[N];
int rad[N], flag[N], pre[N];
void get_rad(char p[], int pos, int lens)
{
int prepos = pos;
p[++pos] = '&';
for (int i = prepos; i >= 1; i--) p[++pos] = p[i];
get_sa(p, pos);
get_height(p, pos);
RMQ_pre(pos);
for (int i = 1; i <= prepos; i++)
{
int x = i, y = pos - i + 1;
int rkx = rk[x], rky = rk[y];
if (rkx > rky) swap(rkx, rky);
rad[i] = RMQ_min(rkx + 1, rky) / 2;
if (x > lens) rad[i] = min(rad[i], x - lens - 1);
}
}
struct BIT_tree{
int treemax;
ll tree[N];
void init() //初始化
{
memset(tree, 0, sizeof tree);
treemax = 100010;
}
inline int lowbit(int x){ return x & (-x); }
void modify(int i, ll x) //单点更新
{
i++;
while(i <= treemax)
{
tree[i] += x;
i += lowbit(i);
}
}
ll query(int i)//前缀和查询
{
i++;
ll s = 0;
while(i > 0)
{
s += tree[i];
i -= lowbit(i);
}
return s;
}
}lencnt[2], addsum[2];
ll get_ans(int pos)
{
ll ans = 0;
map<int, ll>mp[2];
for (int i = 0; i < 2; i++) lencnt[i].init(), addsum[i].init(), mp[i].clear();
for (int i = 1; i <= pos; i++)
{
int lcplen = ht[i];
lcplen -= pre[min(pos, sa[i] + ht[i] - 1)] - pre[sa[i] - 1];
for (int j = 0; j < 2; j++)
{
IT it = mp[j].upper_bound(lcplen);
while (it != mp[j].end())
{
int x = it->first;
ll y = it->second;
lencnt[j].modify(x, -y);
addsum[j].modify(x, -1LL * x * y);
lencnt[j].modify(lcplen, y);
addsum[j].modify(lcplen, 1LL * lcplen * y);
mp[j][lcplen] += y;
mp[j].erase(it++);
}
}
int rlen = rad[sa[i]], cho = 1 - flag[i];
ans += addsum[cho].query(rlen); //先统计小于等于rlen的答案
ans += 1LL * rlen * (lencnt[cho].query(100005) - lencnt[cho].query(rlen));
lencnt[flag[i]].modify(rlen, 1);
addsum[flag[i]].modify(rlen, rlen);
mp[flag[i]][rlen] += 1;
}
return ans;
}
int main()
{
scanf("%s", s + 1);
scanf("%s", t + 1);
int lens = strlen(s + 1), lent = strlen(t + 1);
int pos = 0;
for (int i = 1; i <= lens; i++) p[++pos] = '#', p[++pos] = s[i];
p[++pos] = '#'; p[++pos] = '*';
for (int i = 1; i <= lent; i++) p[++pos] = '#', p[++pos] = t[i];
p[++pos] = '#';
lens = lens << 1 | 1;
lent = lent << 1 | 1;
get_rad(p, pos, lens);
p[pos + 1] = '\0';
get_sa(p, pos);
get_height(p, pos);
for (int i = 1; i <= pos; i++)
{
if (sa[i] <= lens) flag[i] = 0;
else flag[i] = 1;
if (p[i] == '#') pre[i] = 1;
pre[i] += pre[i - 1];
}
ll ans = get_ans(pos);
printf("%lld\n", ans);
return 0;
}
习题5 String 传送门
题意:
给你一个串,求所有不同字串的贡献和,每种字串的贡献,k*(k+1)/2,k为该子串出现的次数
思路:
后缀数组 + 单调栈
1. 对出现大于等于2次的计算,处理方法类似习题2, 利用单调栈和height分类求解即可
2. 对只出现1次的计算,枚举每个串S[i], len = |S[i]|, 则有 len - max(height[i], height[i + 1]) 个串只出现了一次
代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <map>
#include <algorithm>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int sa[N], rk[N], oldrk[N << 1], id[N], px[N], cnt[N], ht[N];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_sa(char s[], int n)
{
int i, m = 300, p, w;
for (int i = 1; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[rk[i] = s[i]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
for (w = 1; w < n; w <<= 1, m = p)
{ // m=p 就是优化计数排序值域
for (p = 0, i = n; i > n - w; --i) id[++p] = i;
for (i = 1; i <= n; ++i)
if (sa[i] > w) id[++p] = sa[i] - w;
for (int i = 0; i <= m; i++) cnt[i] = 0;
for (i = 1; i <= n; ++i) ++cnt[px[i] = rk[id[i]]];
for (i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
for (i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
for (int i = 0; i <= n; i++) oldrk[i] = rk[i];
for (p = 0, i = 1; i <= n; ++i)
rk[sa[i]] = cmp(sa[i], sa[i - 1], w) ? p : ++p;
}
}
void get_height(char s[], int n)
{
for (int i = 1, k = 0; i <= n; ++i)
{
if (k) --k;
while (s[i + k] == s[sa[rk[i] - 1] + k]) ++k;
ht[rk[i]] = k;
}
}
int l[N], r[N], qu[N], tot;
void get_array_lr(int n)
{
ht[0] = ht[n + 1] = -1;
qu[++tot] = 0;
for (int i = 1; i <= n; i++)
{
while (tot && ht[i] <= ht[qu[tot]]) tot--;
l[i] = qu[tot] + 1;
qu[++tot] = i;
}
tot = 0;
qu[++tot] = n + 1;
for (int i = n; i >= 1; i--)
{
while (tot && ht[i] <= ht[qu[tot]]) tot--;
r[i] = qu[tot] - 1;
qu[++tot] = i;
}
ht[0] = ht[n + 1] = 0;
}
char s[N];
vector<int>v[N];
int sum[N];
int main()
{
scanf("%s", s + 1);
int len = strlen(s + 1);
get_sa(s, len);
get_height(s, len);
get_array_lr(len);
ll ans = 0;
for (int i = 1; i <= len; i++) v[ht[i]].push_back(i);
for (int i = len; i >= 1; i--)
{
int rborder = 0;
for (int j = 0; j < v[i].size(); j++)
{
int le = l[v[i][j]], ri = r[v[i][j]];
if (ri <= rborder) continue;
rborder = ri;
int down = max(ht[le - 1], ht[ri + 1]) + 1;
int cs = ri - le + 2;
ans += 1LL * cs * (cs + 1) / 2 * (i + 1 - down);
}
}
for (int i = 1; i <= len; i++)
{
int ma = max(ht[i], ht[i + 1]);
ans += len - sa[i] + 1 - ma;
}
printf("%lld\n", ans);
return 0;
}
附
本人不太会写博客,若有错误,敬请指出,有点丑见谅


$\text{%%%}$