%%% y 总 蒟蒻刚学网络流想着记点笔记 有问题欢迎指正 谢谢各位大佬啦。
网络流的基本概念
1.1流网络,不考虑反向边
在一张有向图中 G = (V, E) 中有一个源点 S 和一个汇点 T。
源点 S 有无限多的水流可以向外流出,汇点 T 可以接受无限多的水流。
其中对于每一条有向边有一个边权代表这条有向边最大可以流过的流量(用 c(u, v) 来表示)。
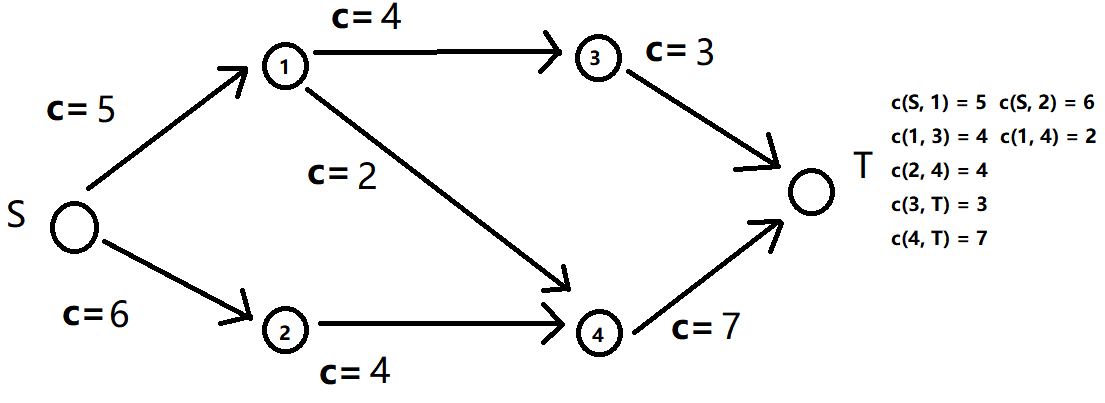
1.2 可行流,不考虑反向边
对于可行流用 f 来表示,f 指的是对于一整张有向图而言,指定有向图中每条有向边流过多少流量。f(u, v) 指的是从 u 到 v 的一条有向边的可行流。
1.2.1 f 满足两个条件:容量限制、流量守恒
{1、容量限制:0≤f(u,v)≤c(u,v)2、流量守恒:∀x∈(V−{S,T})∑∀(v,x)∈Ef(v,x)=∑∀(x,v)∈Ef(x,v)
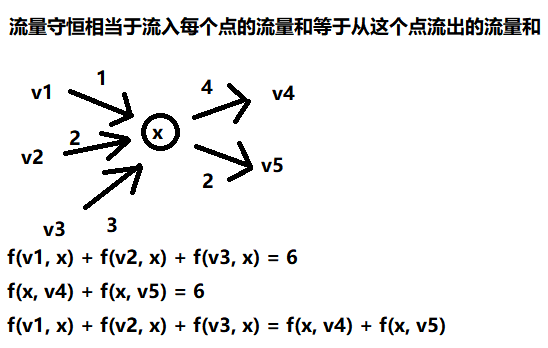
1.2.2 可行流的流量指从源点流出的流量 - 流入源点的流量
|f|=∑(s,v)∈Ef(s,v)−∑(v,s)∈Ef(v,s)
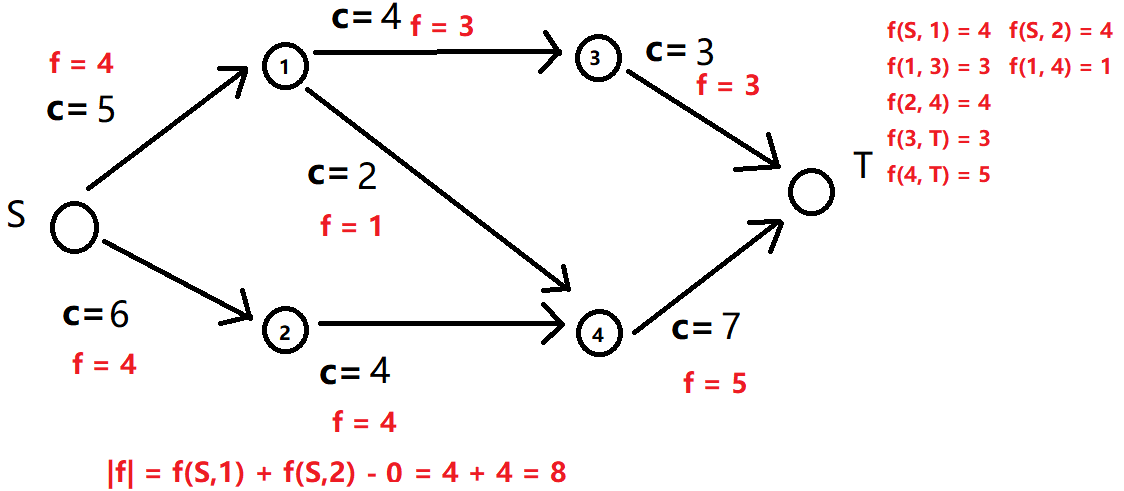
1.2.3 最大流是指最大可行流
1.3 残留网络,考虑反向边
残留网络指的是在原网络中指定了可行流之后对应的一个网络流,原网络的一个可行流对应一个残留网络。
其中残留网络的点包含原网络中的所有点 V 、边包含了原网络中的边 E 和其一一对应的反向边 RE。
残留网络的每条边的边权
∀(u,v)∈E的边权c′(u,v)=c(u,v)−f(u,v)∀(u,v)∈RE的边权c′(u,v)=f(v,u)(∀(v,u)∈E)(这里指的是在原网络E中(v,u)一条边)(在新的残留网络中的c′(u,v)是原网络的一条反向边)
其中上图的可行流 f 对应的残留网络为
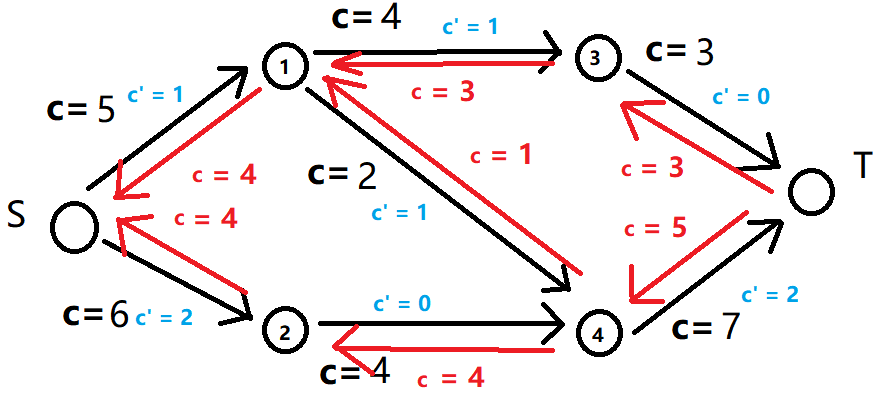
1.3.1残留网络的可行流f’ + 原图的可行流f = 原题的另一个可行流
其中残留网络的可行流 f’ 需满足
{1、容量限制:0≤f′(u,v)≤c′(u,v)2、流量守恒:∀x∈(V−{S,T})∑∀(v,x)∈Ef′(v,x)=∑∀(x,v)∈Ef′(x,v)
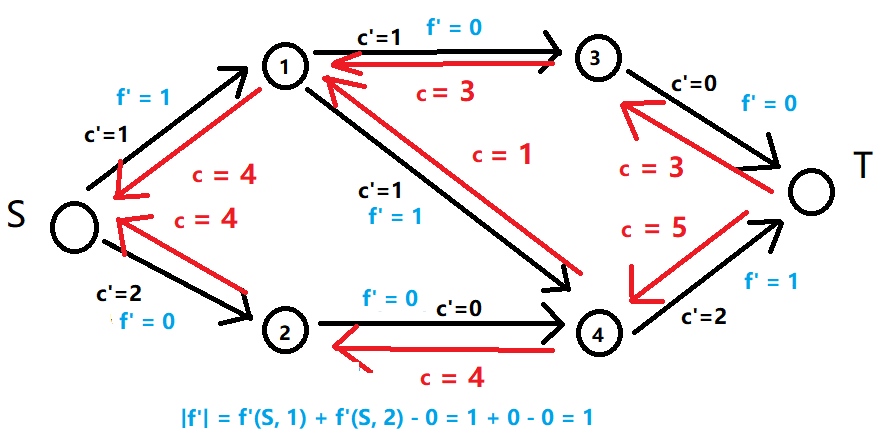
残留网络的可行流f’ + 原图的可行流f = 原题的另一个可行流
f’ + f 需满足
容量限制:∀(u,v)∈E的边权c′(u,v)=c(u,v)−f(u,v)∀(u,v)∈E0≤f′(u,v)≤c′(u,v)c′(u,v)=c(u,v)−f(u,v)0≤f′(u,v)≤(c(u,v)−f(u,v))0≤f′(u,v)+f(u,v)≤c(u,v)
因为f和f′都满足流量守恒∀x∈(V−{S,T})∑∀(v,x)∈Ef′(v,x)+∑∀(v,x)∈Ef(v,x)=∑∀(x,v)∈Ef′(x,v)+∑∀(x,v)∈Ef(x,v)
|f′+f|=|f′|+|f|
结论 残留网络中的任何一个 f’ ,|f’|大于0,都可以更新原网络的可行流。
1.4 增广路径
增广路径指的是在残留网络中有一条路径从源点到汇点,其中的每一条边的残留容量都大于 0 。
1.5 割
1.5.1 割的定义
将原网络中的 V 分成 2 个子集 S 和 T 。且满足 割 的选择有很多种
S⋃T=V,S⋂T=∅同时源点∈S,汇点∈T
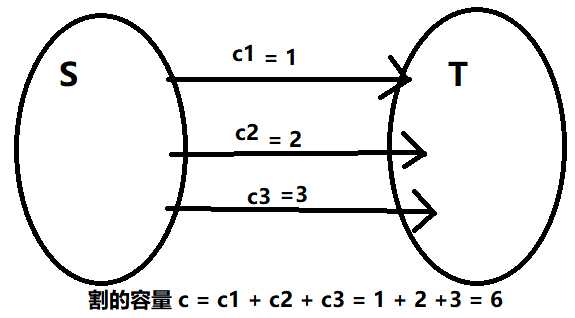
1.5.2 割的容量,不考虑反向边,“最小割”是指容量最小的割。(应该可以类比上面流网络的定义)
割的容量c=∑∀u∈S∑∀v∈Tc(u,v)[(u,v)∈E]
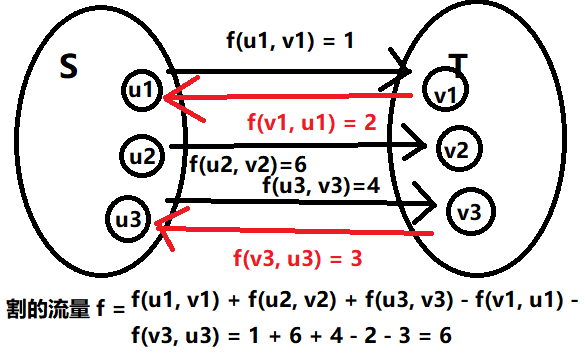
1.5.3 割的流量,考虑反向边,f(S, T) <= c(S, T) , f(S, T) = |f| => |f| <= c(S, T)(应该可以类比上面可行流的定义)
割的流量f=∑∀u∈S∑∀v∈Tf(u,v)[(u,v)∈E]−∑∀v∈S∑∀u∈Tf(v,u)[(v,u)∈E]
性质:
f(X,Y)=−f(Y,X)f(X,X)=0f(Z,X⋃Y)=f(Z,X)+f(Z,Y)f(X⋃Y,Z)=f(X,Z)+f(Y,Z)
f(S,V)=f(S,S⋃T)=f(S,S)+f(S,T)f(S,S)=0=>f(S,T)=f(S,V)f(S,V)=f({源点},V)+f(S−{源点},V)记S′=S−{源点}f(S′,V)=∑∀u∈S′∑∀v∈Vf(u,v)[(u,v)∈E]−∑∀u∈S′∑∀v∈Vf(v,u)[(v,u)∈E]=∑∀u∈S′(∑∀v∈Vf(u,v)[(u,v)∈E]−∑∀v∈Vf(v,u)[(v,u)∈E])(根据可行流的流量守恒性质(∑∀v∈Vf(u,v)[(u,v)∈E]−∑∀v∈Vf(v,u)[(v,u)∈E])=0)也就是f(S−{源点},V)=0=>f(S,T)=f({源点},S)=|f|也就是割的流量=可行流
1.5.6 最大流最小割定理
对于一个网络流而言
(1) 可行流f是最大流
(2) 可行流f的残留网络中不存在增广路
(3) 存在某个割[S, T],|f| = c(S, T)
(1) => (2) 反证法
假设 f 是原网络的一个可行流,同时对应的残留网络中仍然存在一个可行流 f’, 因为 |f + f’| = |f| + |f’| > |f| 这个和定义 f 是最大流矛盾了。
(3) => (1)
因为|f|≤c(S,T)同时最大流是|f|的其中一个值所以最大流≤c(S,T)|f|≤最大流存在某个割[S,T],|f|=c(S,T)≥最大流=>|f|≥最大流=>(1)|f|是最大流
(2) => (3)
Gf 表示原网络中的不存在增广路的残留网络
构造一个割
S :在 Gf 中从源点出发沿容量大于 0 的边走能走到的所有点
T = V - S
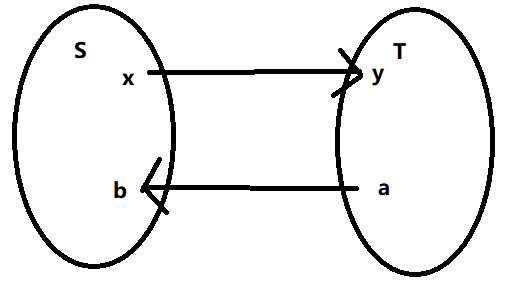
f(x,y)=c(x,y)反证法=>c′(x,y)=c(x,y)−f(x,y)如果c′(x,y)>0也就是源点能够到y,这和S集合的定义矛盾c′(x,y)=0=>f(x,y)=c(x,y)
f(a,b)=0反证法=>c′(b,a)=f(a,b),如果f(a,b)>0也就是c(b,a)>0,和集合S的定义矛盾=>f(a,b)=0
|f|=∑∀u∈S∑∀v∈Tf(u,v)[(u,v)∈E]−∑∀v∈S∑∀u∈Tf(v,u)[(v,u)∈E]∑∀u∈S∑∀v∈Tf(u,v)[(u,v)∈E]=∑∀u∈S∑∀v∈Tc(u,v)[(u,v)∈E]=c(S,T)∑∀v∈S∑∀u∈Tf(v,u)[(v,u)∈E]=0=>|f|=c(S,T)
最大流 = 最小割
最大流=最小割因为最小割是c(S,T)中的一个值所以最大流≤最小割=>最大流≤最小割最小割≤c(S,T)=|f|≤最大流=>最小割≤最大流所以最大流=最小割
EK算法
while(){
找增广路;
更新残留网络
}
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N = 1010, M = 20010;
const int inf = 0x3f3f3f3f;
int h[N], ne[M], e[M], w[M], idx;
int n, m, S, T, maxflow, pre[N], incf[N], vis[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
// 找一条增广路
int bfs()
{
memset(vis, 0, sizeof vis);
queue < int > q;
q.push(S);vis[S] = 1;
incf[S] = inf; // 从源点可以有无限量的水流出来
while(q.size()){
int u = q.front();q.pop();
for(int i = h[u]; ~i; i = ne[i]){
if(w[i]){ // 根据增广路的定义 只有当前边的容量大于 0
int v = e[i];
if(vis[v]) continue;
incf[v] = min(w[i], incf[u]);//一条增广路上流过的最大可行流受到每条边的最小容量限制
pre[v] = i; // 记录当前点的前驱
q.push(v), vis[v] = 1;
if(v == T) return 1;
}
}
}
return 0;
}
// 更新残留网络
void update()
{
int x = T;
while(x != S){
int i = pre[x];
w[i] -= incf[T]; // c(u, v) 的容量减去找到的增广路上的最小容量
w[i ^ 1] += incf[T]; // (u, v)的方向边加上找到的增广路上的最小容量
x = e[i ^ 1];
}
maxflow += incf[T]; // 累加所有增广路的最大可行流
}
int main()
{
cin >> n >> m >> S >> T;
memset(h, -1, sizeof h);
for(int i = 1; i <= m; i ++ ){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, 0);
}
while(bfs()) update();
cout << maxflow << endl;
return 0;
}
Dinic算法
while(){
一次找多条增广路,通过分层图;
更新残留网络
}
1、当前弧优化
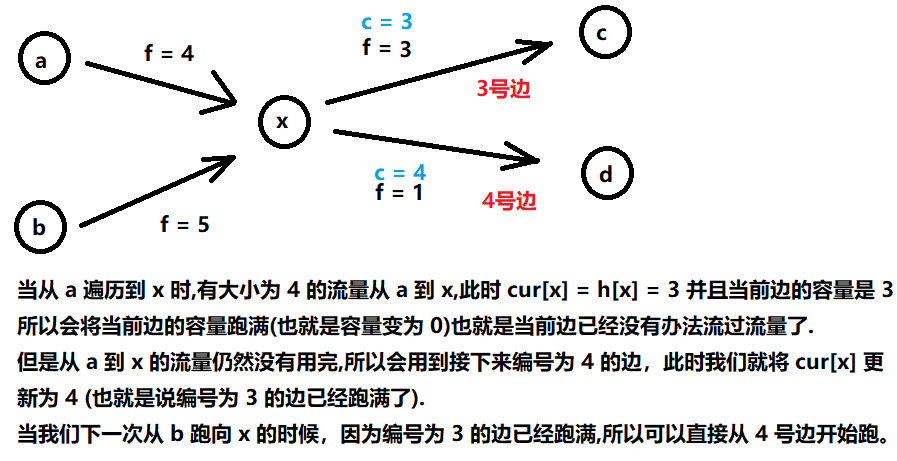
2号优化 (不知道叫什么名字)
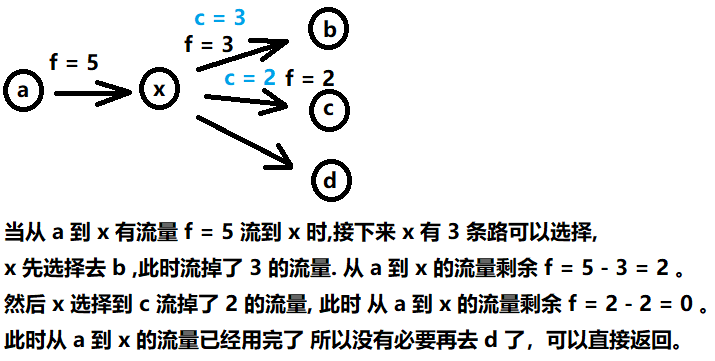
3号优化

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1e4 + 10, M = 2e5 + 10, inf = 0x3f3f3f3f;
int h[N], ne[M], e[M], w[M], idx;
int n, m, S, T, cur[N], d[N], q[N];
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
// 找增广路 同时将图变成分层图,方便处理环
int bfs()
{
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
d[S] = 0, q[0] = S, cur[S] = h[S];
while(hh <= tt){
int u = q[hh ++ ];
for(int i = h[u]; ~i; i = ne[i]){
if(w[i] && d[e[i]] == -1){
d[e[i]] = d[u] + 1;
cur[e[i]] = h[e[i]];
if(e[i] == T) return 1;
q[++ tt] = e[i];
}
}
}
return 0;
}
// 更新残留网络
int dfs(int u, int flow)
{
if(u == T) return flow;
int rest = 0, k;
for(int i = cur[u]; ~i; i = ne[i]){
cur[u] = i; // 当前弧优化
if(w[i] && d[e[i]] == d[u] + 1){
k = dfs(e[i], min(flow - rest, w[i]));
if(!k) d[e[i]] = -1; // 3号优化,将分层图中的当前点变成 -1 相当于打上标记
w[i] -= k, w[i ^ 1] += k, rest += k;
if(rest == flow) return flow; // 2号优化
}
}
return rest;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = dfs(S, inf)) res += flow;
return res;
}
int main()
{
cin >> n >> m >> S >> T;
memset(h, -1, sizeof h);
for(int i = 1; i <= m; i ++ ){
int a, b, c;
scanf("%d %d %d", &a, &b, &c);
add(a, b, c), add(b, a, 0);
}
printf("%d\n", dinic());
return 0;
}


图错了吧
1.5.3性质那块的公式倒数第二行也就是f(S,T)=f(源点,S)=|f|,应该是f(S,T)=f(源点,V)=|f|吧
%%%
公式很赞
# 这必须素质三连
####赞