二，线段树
线段树又称区间树，是一种基于分治思想的二叉树结构，每个节点代表一段区间，和按照利用二进制性质划分区间的树状数组相比，线段树是一种更加通用的数据结构。
以下来自《算法竞赛进阶指南》
- 线段树的每个节点代表一个区间
- 线段树具有唯一的根节点，代表的区间是整个统计范围，如[1 , N].
- 线段树的每个叶子节点代表一个长度位一的元区间[x,x].
- 对于每个内部节点[l,r],它的左儿子是[l ,mid],右儿子[mid + 1 , r], 其中 mid = (l + r) / 2 (下取整)
一般线段树树形结构如下图所示
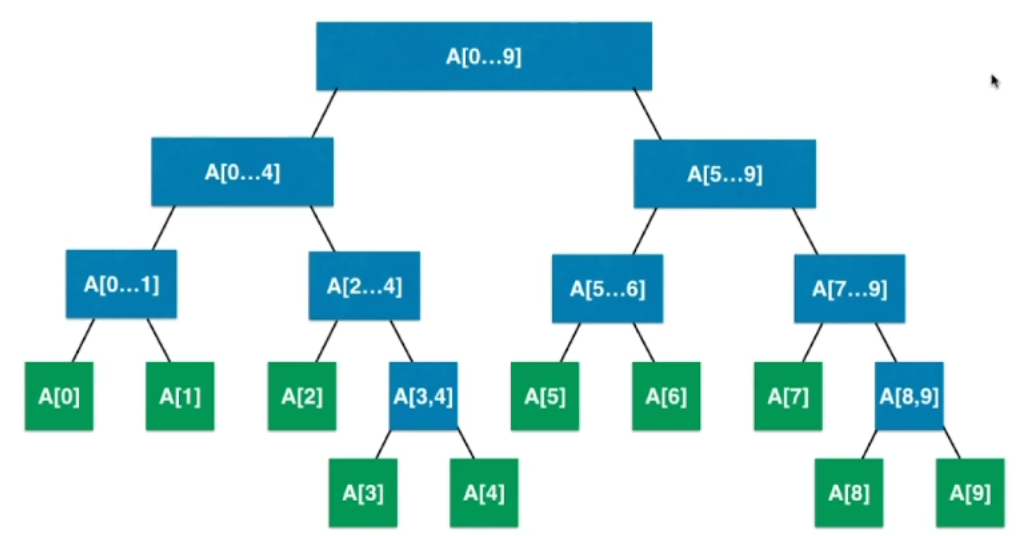该图片来源网络
每个节点表示该节点表示区间的某种属性可以是和也可以是最大值，以下是表示最大值的线段树结构
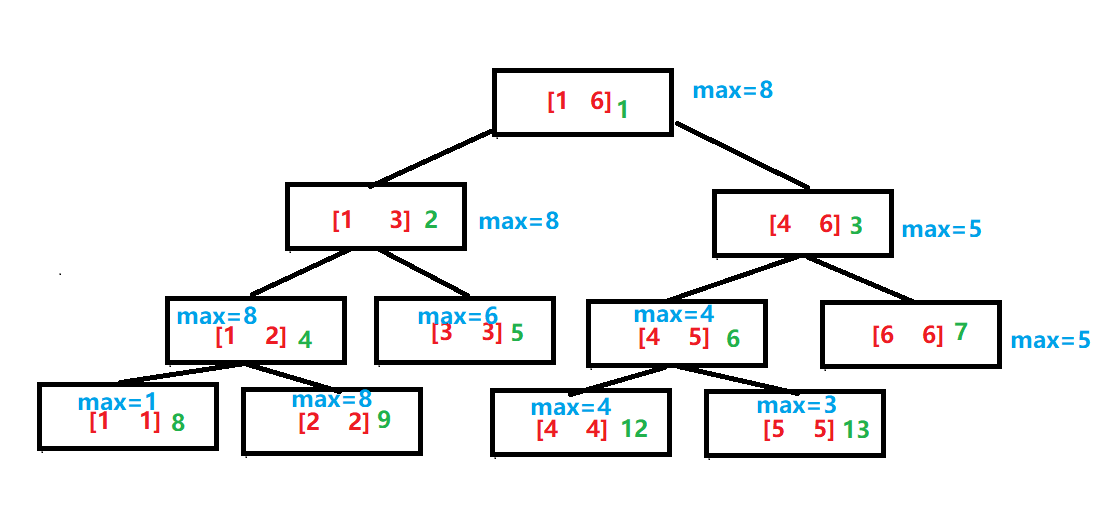
图片来源网络
1. 线段树的基本操作以及最大区间和
建树
struct Tree{
int l, r; //表示该节点区间左右边界
int val; // 代表该区间特征的某个值 ，如最大值，区间和等等。。。。
}
int a[N] , 叶子节点的值
void pushup(int u){ // 往上推
tr[u].val = tr[u << 1].val + tr[u << 1].val; // 用区间和做示范，具体依据情况而定
// tr[u].val = max(tr[u << 1].val , tr[u << 1].val); 求区间最大值
}
void build(int u,int l,int r){
if(l == r)tr[u] = {l ,r ，a[i]};
else
{
int mid = l + r >> 1;
tr[u] = {l , r, 0};
build(u << 1 , l ,mid),build(u << 1 , mid + 1 , r); // 递归建立左右子树，从下而上建树
pushup(u);
}
}
单点修改
void change(int u,int x,int d){
if(tr[u ].l == x && tr[u].r == x)
{
tr[u].val += d;
return ;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid)change(u << 1 , x , d);
else change(u << 1 | 1 , x, d); // 往有交集的区间递归修改
pushup(u); // 修改完成后还要往上推
}
}
区间查询
int query(int u,int l,int r){
if(tr[u].l >= l && tr[u].r <= r)return tr[u].val; // 只有在查询区间的的节点才会返回
else
{
int val = 0;
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid)val = max(val, query(u << 1 , l ,r)) // or val + query(u << 1 , l ,r)
if(r > mid )val = max(val, query(u << 1 | 1 , l ,r)) // or val + query(u << 1 | 1, l ,r)
return sum;
}
}
求区间最大和
对于处理区间最大和，我们只要对区间代表元素，以及对往上推（pushup)，做相应变化即可
如下图所示
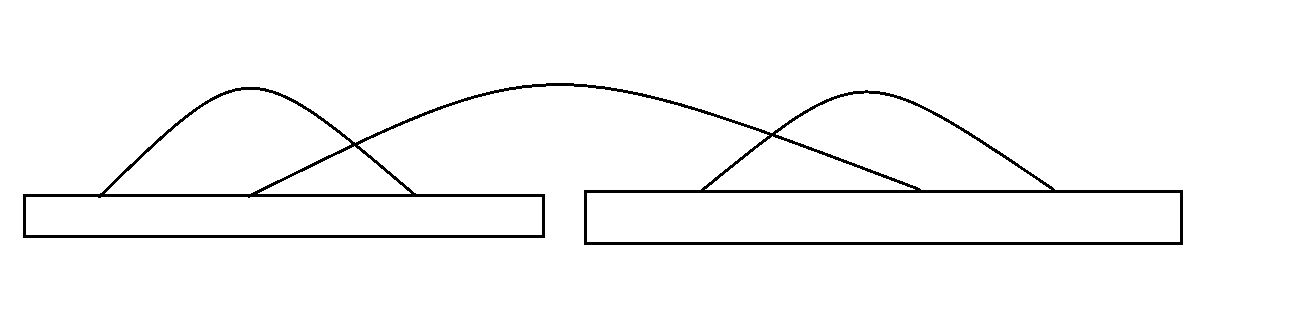
最大连续区间和可能是三者之一，我们维护区间最大和时还要维护左右边界的最大和
接下来直接上代码吧
题目链接： 你能回答这些问题吗？
#include <iostream>
using namespace std;
const int N = 5e5 + 10, INT_MIN = -1e9 ;
struct Tree{
int l,r;
int sum , ld , rd,md;
}tr[4 * N];
int n,m;
int a[N];
void
void pushup(int u){
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
tr[u].ld = max(tr[u << 1].ld , tr[u << 1].sum + tr[u << 1 | 1].ld);
tr[u].rd = max(tr[u << 1].rd , tr[u << 1 | 1].sum + tr[u << 1].rd);
tr[u].md = max(tr[u << 1].md , max(tr[u << 1 | 1].md , tr[u << 1].rd + tr[u << 1 | 1].ld));
}
void build(int u ,int l ,int r){
if(l == r)tr[u] = {l , r, a[l],a[l], a[l],a[l]};
else
{
tr[u ] = {l ,r, 0,0};
int mid = l + r >> 1;
build(u << 1 , l , mid),build(u << 1 | 1 , mid + 1 , r);
pushup(u);
}
}
Tree query(int u ,int l,int r){
if (tr[u].l >= l && tr[u].r <= r) return tr[u];
else
{
int mid = tr[u].l + tr[u].r >> 1;
if (r <= mid) return query(u << 1, l, r);
else if (l > mid) return query(u << 1 | 1, l, r);
else
{
auto left = query(u << 1, l, r);
auto right = query(u << 1 | 1, l, r);
Tree res;
pushup(res, left, right);
return res;
}
}
}
void change(int u,int x,int d){
if(tr[u].r == tr[u].l )
{
tr[u].sum = d;
return;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid)change(u << 1 , x ,d);
else change(u << 1 | 1 , x, d);
pushup(u);
}
}
int main(){
cin >> n >> m;
for(int i = 1 ; i <= n ;i++)cin >> a[i];
build(1,1,n);
int k,l,r;
while(m--)
{
cin >> k;
if( k == 1)
{
cin >> l >> r;
cout << query(1 ,l ,r ).md << endl;
}
else
{
cin >> l>> r;
change(1,l,r);
}
}
return 0;
}
2. 线段树求区间最大公约数
题目链接： 区间最大公约数
依题意来看这道题看似需要区间修改和区间查询，实际上，我们利用相关性质就能用单点修改，区间查询来轻而易举化解它， 我们可以利用差分来实现所谓的区间修改，例如我们要查询区间[4, 8]的公约数，那么GCD(A[4] , GCD([1 , 8]的差分元素))就是所求答案
上代码
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
typedef long long LL;
const int N = 5e5 + 10;
struct Tree{
int l,r;
LL sum , d;
}tr[4 * N];
int n,m;
LL a[N];
LL gcd(LL a,LL b){
return b == 0 ? a : gcd(b,a % b);
}
void pushup(Tree& u,Tree& l ,Tree& r){
u.sum = l.sum + r.sum;
u.d = gcd(l.d,r.d);
}
void pushup(int u){
pushup(tr[u], tr[u << 1] ,tr[u << 1 | 1] );
}
void build(int u,int l,int r)
{
if(l == r){
LL d = a[r] - a[r - 1];
tr[u] = {l,r,d,d};
}
else
{
tr[u].l = l , tr[u].r = r;
int mid = l + r >> 1;
build(u << 1 , l , mid);
build(u << 1 | 1 , mid + 1 , r);
pushup(u);
}
}
void modify(int u ,int x,LL d){
if(tr[u].l == x && tr[u].r == x)
{
LL v = tr[u].sum + d;
tr[u].sum = v;
tr[u].d = v;
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid)modify(u << 1 , x , d);
else modify(u << 1 | 1 , x , d);
pushup(u);
}
}
Tree query(int u ,int l,int r){
if(tr[u].l >= l && tr[u].r <= r)
{
return tr[u];
}
else
{
int mid = tr[u].l + tr[u].r >> 1;
if(r <= mid)return query(u << 1 , l , r);
else if(l > mid )return query(u << 1 | 1 , l ,r);
else
{
Tree res;
auto left = query(u << 1 , l ,r);
auto right = query(u << 1 | 1 , l , r);
pushup(res,left, right);
return res;
}
}
}
int main(){
cin >> n >> m;
for(int i = 1 ; i <= n ;i++)cin >> a[i];
build(1,1,n);
char op;
int l ,r ;
LL d;
while(m -- )
{
cin >> op ;
if(op == 'Q')
{
cin >> l >> r;
cout << abs(gcd(query(1,1 ,l ).sum , query(1,l + 1 , r).d) )<< endl;
}
else
{
cin >> l >> r >> d;
modify(1,l, d) ;
if(r + 1 <= n)modify(1,r + 1 , -d);
}
}
return 0;
}
3. 线段树区间修改，区间查询
多维护一个懒标记即可，延迟修改子节点
代码
例题
题目链接： 一个简单的整数问题二
#include <iostream>
using namespace std;
const long long N = 1e5 + 10;
struct Tree{
long long l,r;
long long sum , lazy;
}tr[4 * N];
long long n,m;
long long a[N];
void spread(long long u){
if(tr[u].lazy)
{
tr[u << 1].sum += tr[u].lazy * (tr[u << 1].r - tr[u << 1].l + 1);
tr[u << 1 | 1].sum += tr[u].lazy * (tr[u << 1 | 1].r - tr[u << 1 | 1].l + 1);
tr[u << 1 ].lazy += tr[u].lazy;
tr[u << 1 | 1].lazy += tr[u].lazy;
tr[u ].lazy = 0;
}
}
void pushup(Tree& u , Tree& l , Tree& r){
u.sum = l.sum + r.sum;
}
void pushup(long long u){
pushup(tr[u] , tr[u << 1] , tr[u << 1 | 1]);
}
void build(long long u , long long l ,long long r){
if(l == r)tr[u] = {l,r,a[l],0};
else
{
tr[u].l = l , tr[u].r = r;
long long mid = l + r >> 1;
build(u << 1 , l , mid);
build(u << 1 | 1 , mid + 1 , r);
pushup(u);
}
}
long long query(long long u , long long l ,long long r){
if(tr[u].l >= l && tr[u].r <= r)
{
return tr[u].sum;
}
else
{
spread(u);
long long mid = tr[u].l + tr[u].r >> 1;
long long sum = 0;
if(l <= mid)sum += query(u << 1 , l,r);
if(r > mid)sum += query(u << 1 | 1 , l ,r);
return sum;
}
}
void change(long long u ,long long l , long long r,long long d){
if(tr[u].l >= l && tr[u].r <= r)
{
tr[u].sum += d * (tr[u].r - tr[u ].l + 1);
tr[u].lazy += d;
return;
}
else
{
spread(u);
long long mid = tr[u].l + tr[u].r >> 1;
if(l <= mid)change(u << 1 , l ,r ,d);
if (r > mid)change(u << 1 | 1 , l , r, d);
pushup(u);
}
}
int main(){
cin >> n >> m;
for(long long i = 1 ; i <= n ;i++)cin >> a[i];
build(1,1,n);
char op;
long long l,r,d;
while(m--)
{
cin >> op;
if(op == 'C')
{
cin >> l >> r >> d;
change(1,l,r,d);
}
else
{
cin >> l >> r;
cout << query(1,l,r)<<endl;
}
}
return 0;
}
4. 线段树动态开点及合并
为了降低空间复杂度，我们可以不建出整棵树的结构，需要时才建立，不过最初需要建立一个根节点代表整个区间，单我们需要用到某个区间才建立相应的节点，当然这只是一种建树方式，如果题目并不是所有区间都会用到，采用这种方法最佳，实现也很简单。
题目链接： 最大数
#include <iostream>
using namespace std;
const long long N = 1e5;
struct Segment{
long long lc,rc;
long long dat;
}tr[4 * N ];
long long root,tot;
long long p,m;
long long cnt = 1;
long long build(){
tot++;
tr[tot].lc = tr[tot].rc = tr[tot].dat = 0;
return tot;
}
void insert(long long p,long long l,long long r,long long val,long long delta){
if(l == r)
{
tr[p].dat = delta;
return;
}
long long mid = (l + r) /2;
if( val <= mid)
{
if(!tr[p].lc)tr[p].lc = build();
insert(tr[p].lc , l,mid ,val ,delta);
}
else
{
if(!tr[p].rc)tr[p].rc = build();
insert(tr[p].rc , mid + 1,r ,val ,delta);
}
tr[p].dat = max(tr[tr[p].rc].dat, tr[tr[p].lc].dat);
}
long long ask(long long p,long long l,long long r,long long x,long long y){
if(l >= x && r <= y)return tr[p].dat;
else
{
long long mid = (l + r )/ 2;
long long val = 0;
if(x <= mid)val = max(val , ask(tr[p].lc,l,mid,x,y));
if(y > mid)val = max(val,ask(tr[p].rc,mid + 1 , r,x,y));
return val;
}
}
int main(){
cin >> m>> p;
root = build();
char op;
long long x;
long long a = 0;
for(long long i = 0 ; i < m ;i++)
{
cin >> op;
if(op == 'A')
{
cin >> x;
insert(root,1,m,cnt++,(x + a)%p);
}
else {
cin >> x;
a = ask(root,1,m,cnt - x ,cnt - 1);
cout << a << endl;
}
}
return 0;
}
线段树合并
暂时还不知道有什么用，只留一个模板
int merge(int p,int q,int l,int r){
if(!p)return q;
if(!q)return p;
if( l == r)
{
tr[p].dat += tr[q].dat;
return p;
}
int mid = l + r >> 1;
tr[p].lc = merge(tr[p].lc,tr[q].lc,l ,mid);
tr[p].rc = merge(tr[p].rc,tr[q].rc,mid + 1 , r);
tr[p].dat = max(tr[tr[p].lc].dat,tr[tr[p].rc].dat);
return p;
}
写的真的很好