一,树状数组
树状数组是一种利用二进制分解模拟树形结构,从而实现可以在对数时间查询区间和,单点修改的数据结构(区间修改实际上也是单点修改,只不过利用差分的思想)
基本原理
我们都知道在计算机中一个数是由二进制表示的,那么根据任意正整数关于的二的不重复次冥的唯一分解性质,若一个正整数X的二进制分解次冥表示为 AK , AK - 1 ,...., A2 , A1,那么该数X = 2 ^ AK + 2 ^ AK - 1 +…+2^A2 + 2 ^ A1;我们据此可以将[1 , X]分成如下所示若干个小区间:
- 长度为2 ^ A1 的小区间 [1 , 2 ^ A1]
- 长度为2 ^ A2 的小区间 [1 , 2 ^ A1 + 2 ^ A2]
- 长度为2 ^ A3 的小区间 [1 , 2 ^ A1 + 2 ^ A2 + 2 ^ A3]
- 长度为2 ^ A4 的小区间 [1 , 2 ^ A1 + 2 ^ A2 + 2 ^ A3 + 2 ^ A4]
.................
K. 长度为2 ^ AK1 的小区间 [1 , 2 ^ A1 + 2 ^ A2 + 2 ^ A3 + 2 ^ A4 + ...... + 2 ^ AK]
用更直观的图表示:
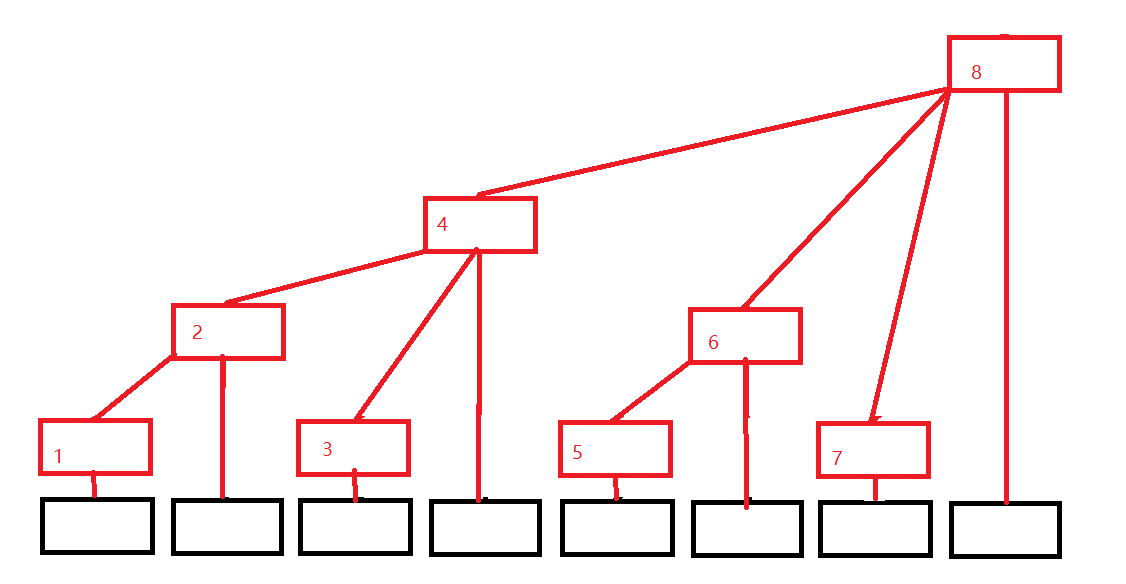
可以得出以下信息
C[1] = A[1];
C[2] = A[1] + A[2];
C[3] = A[3];
C[4] = A[1] + A[2] + A[3] + A[4];
C[5] = A[5];
C[6] = A[5] + A[6];
C[7] = A[7];
C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
显然这棵树是有规律的 即C[i] = A[i - 2k+1] + A[i - 2k+2] + … + A[i];C[i]这个位置存的是[i - 2 ^ k + 1 , i] //k为i的二进制中从最低位到高位连续零的长度
我们可以通过lowbit(x) : x & -x 来算C[i]所表示的区间的大小 即 2 ^ k (k 为最后一位一后面0的个数)
性质
- 每个内部节点保存以它为根所有叶节点的和
- 除树根外的每个内部节点C[x]的父节点为C[x + lowbit(x)]
- 树的深度是o(logn)
- 除叶子节点外,每个子节点的个数等于lowbit(x)的位数
----引用自《算法竞赛进阶指南》
1,树状数组求基本操作(求区间和)
查询区间和
int ask(int x){
int sum = 0;
for( ; x; x -= lowbit(x) )sum += tr[x];
return sum;
}
查询[l , r]的区间和: cout << ask(r) - ask(l) << endl;
修改
void add(int x){
for( ; x; x += lowbit(x))tr[x] += d;
}
给A[2]加上一个数 : add(2 , 1); // A[2] += 1 , 所以父节点也要改变
把A[2]改成某个数:add(2,-A[2] + 1) // A[2] = 1
例题,
题目链接: 校门外的树
题目大意:看某个区间种了多少树
解析:将每次种树的范围对于两个括号 即改(:开始位置 ):结束位置 建立两个树状数组,一个维护左括号,一个右边括号,具体看代码,一目了然
#include <iostream>
using namespace std;
const int N = 5 * 1e4 + 10;
int n,m;
int tr1[N], tr2[N];
int lowbit(int x)
{
return -x & x;
}
void add(int c[],int x , int d)
{
for( ;x <= n ; x += lowbit(x))c[x] += d;
}
int ask(int c[] ,int x){
int sum = 0;
for(; x;x -= lowbit(x) )sum += c[x];
return sum;
}
int pre(int x){
return ask(tr1 , x) * (x + 1) - ask(tr2 , x);
}
int main(){
cin >> n >> m;
int op , l ,r;
while(m --)
{
cin >> op;
if(op == 1)
{
cin >> l >> r;
add(tr1, l ,1);
add(tr2 , r ,1);
}
else
{
cin >> l >> r;
cout << ask(tr1 ,r) - ask(tr2 ,l - 1) << endl;
}
}
return 0;
}
2,树状数组求逆序对
维护一个值域 , 从后往前扫,查询[0 , 当前数 - 1]子区间内有多少个数,即后面有多少个数小于自己,查询完后面,在将自己值域里的那个位置加一,声明[当前数,当前数]这个值域内已经多了一个数
注意:如果数据范围过大,但是只有少量的数,我们可以利用离散化映射到一个小的值域。
上代码
......
int main{
.........
for(int i = n ; i >= 1 ;i--)
{
ans += ask(a[i] - 1);
add(a[i] , 1);
}
.....
return 0;
}
例题
例题一,
题目链接:火柴排队
题目大意:有两列火柴,只能移动相同列中的邻近的火柴,问最小移动多少下使∑i=1n(ai−bi)^2最大
:贪心+逆序对。分析如下:对距离公式化简得:
∑(ai-bi)2=∑(ai2-2aibi+bi2)=∑ai2+∑bi2-2∑aibi,要求∑(ai-bi)2最小,就只需要∑aibi最大即可。这里有个贪心,当 a1[HTML_REMOVED]b,c>d,且ac+bd[HTML_REMOVED]b矛盾,所以若a>b,c>d,则ac+bd>ad+bc
将此式子进行推广:
当a1<a2<a3<…<an ,b1<b2<…<bn的情况下∑aibi最大,即∑(ai-bi)2最小。
然后,将两个序列分别排序,确定每对数的对应关系,明显,同时移动两个序列中的数等效于只移动一个序列中的数,移动的时候可以将一个火柴序列不动,只移动另外一个序列。
于是可以构造一个数组C,C[i]表示最初的第i个数应该移动到C[i]位置。于是问题转换成对C[i]数组排序,每次可以交换相邻两个数,问最少需要移动多少次的问题了,也就是求这个序列的逆序对数量的问题(这里用归并排序思想实现)。
– 来源ssoj官网题解;
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10 , mod = 99999997;
struct Node{
int x,i;
bool operator<(const Node& v)const{
return x < v.x;
}
}a[N],b[N];
int n;
int h[mod];
int tr[N];
inline int lowbit(int x){
return -x & x;
}
int ask(int x){
int sum = 0 ;
for( ; x ; x -= lowbit(x))sum += tr[x];
return sum;
}
void add(int x,int d){
for( ; x <= n ; x += lowbit(x))tr[x] += d;
}
int main(){
cin >> n;
for(int i = 1 ; i <= n ;++i)
{
cin >> a[i].x;
a[i].i = i;
}
for(int i = 1 ; i <= n ; ++i)
{
cin >> b[i].x;
b[i].i = i;
}
sort(a + 1, a + n + 1 );
sort(b + 1, b + n + 1);
for(int i = 1 ; i <= n ;++i)
{
h[a[i].i] = b[i].i;
}
int ans = 0;
for(int i = n ; i >= 1; --i )
{
ans = (1ll * ans + ask(h[i] - 1) ) % mod;
add(h[i], 1);
}
cout << ans << endl;
return 0;
}
例题二,
题目链接:小朋友排队
题目大意:调换小朋友的位置,按矮到高站队,每次调换这个小朋友就不高兴程度就加一。
解析:扫描两次求每个小朋友后面有多少个比他矮,前面有多少个比他高就行了。。。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
const int N = 1000011,H = 100010;
int tr[N],h[H],sum[H];
int lowbit(int x){
return x&-x;
}
void add(int x){
for(int i = x ; i <= N ; i+=lowbit(i) )tr[i]+=1;
}
int query(int x){
int res = 0;
for(int i = x ; i ; i-=lowbit(i))res+=tr[i];
return res;
}
int main(){
int n;
cin>>n;
for(int i = 0 ; i < n ; i++)scanf("%d",&h[i]),h[i]++;
for(int i = 0 ; i < n ; i++)
{
sum[i]=query(N-1)-query(h[i]);
add(h[i]);
}
memset(tr,0,sizeof(tr));
for(int i = n - 1 ; i >=0 ; i--)
{
sum[i]+=query(h[i]-1);
add(h[i]);
}
LL res = 0;
for(int i = 0 ; i < n ; i++)res+=(LL)sum[i]*(sum[i]+1)/2;
cout<<res<<endl;
return 0;
}
3. 树状数组区间修改,单点查询
维护一个差分序列即可
int ask(){
......
}
void add(){
...
}
int main(){
.........
for(int i = 1 ; i <= n ;i++)
{
add(i , a[i] - a[i - 1]);
}
add(3 , 5) ,add(5 , -5) // 区间[3 , 4] 每个加5
cout << ask(5); // 查询a[5]的值
........
return 0;
}
例题
例题一。
题目链接:简单题
题目大意:顾名思义就是一道简单题。
题目解析:维护差分序列,每个位置记录翻转次数即可,答案模二
代码
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n,m;
int a[N];
int tr[N];
int lowbit(int x){
return -x & x;
}
int ask(int x){
int sum = 0;
for( ; x ; x -= lowbit(x))sum += tr[x];
return sum;
}
void add(int x,int d)
{
for( ; x <= n;x += lowbit(x))tr[x] += d;
}
int main(){
cin >> n >> m;
int op;
int l,r,x;
while(m--){
cin >> op;
if(op == 1)
{
cin >> l >> r;
add(l,1) , add(r + 1 , -1);
}
else
{
cin >> x;
cout << ask(x) % 2 << endl;
}
}
return 0;
}
4. 树状数组区间修改,区间查询
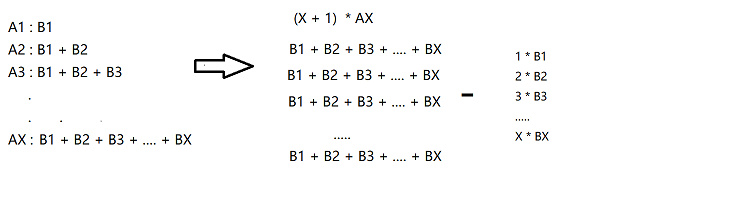
由上图可知,实现区间修改,区间查询,只需要维护两个树状数组即可
例题
题目链接 一个简单的整数问题2 :
#include <iostream>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n,q;
LL tr1[N],tr2[N];
int a[N];
int lowbit(int x){
return -x & x;
}
void add(LL tr[],int x,LL d){
for( ; x <= n ; x += lowbit(x))tr[x] += d;
}
LL ask(LL tr[],int x)
{
LL sum = 0;
for(; x; x -= lowbit(x) )sum += tr[x];
return sum;
}
LL prefix_sum(int x)
{
return ask(tr1, x) * (x + 1) - ask(tr2, x);
}
int main(){
cin >> n >> q;
for(int i = 1 ; i <= n; i++){
cin >> a[i];
add(tr1, i, a[i] - a[i - 1]);
add(tr2, i, (LL)(a[i] - a[i - 1]) * i);
}
char op;
int l ,r , d;
while(q--)
{
cin >> op;
if(op == 'Q')
{
cin >> l >> r;
cout << prefix_sum(r) - prefix_sum(l - 1) << endl;
}
else
{
cin >> l >> r >> d;
add(tr1, l, d), add(tr2, l, l * d);
// a[r + 1] -= d
add(tr1, r + 1, -d), add(tr2, r + 1, (r + 1) * -d);
}
}
return 0;
}
二维树状数组
将每一列当成区间的一个元素来理解即可,操作和一维的一样
例题
打鼹鼠
代码:
#include <iostream>
using namespace std;
const int N = 1024 + 10;
int n , op;
int tr[N][N];
int lowbit(int x){
return -x & x;
}
int ask(int x,int y)
{
int sum = 0;
for( int i = x; i ;i -= lowbit(i) )
for(int j = y ; j ; j -= lowbit(j))
sum += tr[i][j];
return sum;
}
void add(int x,int y,int d){
for(int i = x ; i <= n; i += lowbit(i))
for(int j = y ; j <= n ; j += lowbit(j))
tr[i][j] += d;
}
int main(){
cin >> n;
int x,y,k,y2,x2;
while(cin >> op, op != 3)
{
if(op == 1)
{
cin >> x >> y >> k;
x++,y++;
add(x,y,k);
}
else if(op == 2)
{
cin >> x >> y >> x2 >> y2;
x++,y++, x2++,y2++;
cout << ask(x2 , y2) - ask(x - 1,y2) - ask(x2 , y - 1) + ask(x -1 , y - 1) << endl;
}
}
return 0;
}


NB!!!
太强了,果断收藏