第五期:BFS(宽搜) 


蓝桥杯热门考点模板总结来啦 ~
~
你绝绝绝绝绝绝对不能错过的常考BFS模板 
![]()
![]()
![]()
冲刺蓝桥杯省一模板大全来啦  ~
~
蓝桥杯4月8号就要开始了  ~
~
距离蓝桥杯省赛倒数第5天 


还不清楚BFS(宽搜) 的同学快快看过来!!!
还没背熟模板的伙伴们背起来 


真题千千万万遍,蓝桥省一自然现! 
祝大家4月8号蓝桥杯上岸  ~
~
不清楚蓝桥杯考什么的点点下方
考点秘籍
蓝桥杯竞赛干货
算法竞赛字符串常用操作总结!!!
往期回顾
蓝桥杯上岸每日N题第一期(一)!!!
蓝桥杯上岸每日N题第一期(二)!!!
蓝桥杯上岸每日N题第一期(三)!!!
蓝桥杯上岸每日N题第二期(一)!!!
蓝桥杯上岸每日N题第三期(一)!!!
蓝桥杯上岸必刷专题
蓝桥杯上岸必刷!!!(日期专题+保姆级教学)
蓝桥杯上岸必刷!!!(字符串专题)
蓝桥杯上岸必刷!!!(模拟/枚举专题)
想背纯享模版的伙伴们点点下方
蓝桥杯省一你一定不能错过的模板大全(第一期)
蓝桥杯省一你一定不能错过的模板大全(第二期)
想背注释模版的伙伴们点点下方
蓝桥杯必背第一期
蓝桥杯必背第二期
蓝桥杯上岸必背!!! (第三期 DP)
蓝桥杯上岸必背!!!(第四期DFS)
想看JavaB组填空题的伙伴们点点下方 
填空题
DFS/BFS是蓝桥杯的热门考点,距离省赛仅剩5天,干就完事了 
下面让我们开始刷起来 


DFS你的大脑,BFS你的体力 


让我们一起上岸蓝桥杯 
BFS小结:
所用的数据结构:队列
如何维护?
队列维护一层一层往外搜索的操作:
tt=-1;
hh=0;
q[++tt]=new PII(x,y)
像一些需要对坐标进行操作的需要用到结构体
q[++tt]=*;
一些不需要结构体的直接插入即可
手写插入
while(hh<=tt){
t=q[hh++];
//取出队头后再对队头元素进行操作
//操作新元素视题目而定
//再将新元素入队,用于下一次出队
}
java容器
Queue<数据类型>q=new LinkedList<>();
while(hh<=tt){
t=queue.poll();
//取出队头后再对队头元素进行操作
//操作新元素视题目而定
//再将新元素入队,用于下一次出队
queue.add(*);
}
梗要:取出队头元素,再对队头元素进行操作,再入队,一层一层往外搜,先搜到的一定是最短的点。
走迷宫 (经典模型)
分析
BFS用于求解最短路问题,且各边权重全为1(相等),一层一层往外搜。
运用BFS+队列,从起点走到终点,先到终点的即为最短距离。
BFS:搜索(满足条件)
队列:将满足条件的点入队,通过出队、入队的操作,一层一层往外扩展。
如:第一层搜到的为距离1,第二层为距离2,以此类推。
走迷宫:
同时满足以下条件:
(1)x,y大于等于0并且x<n,y<m不越界
(2)走到的点为0,不为1。
g[x][y]=0;
(3)走到的位置还没被走过
d[x][y]=-1;
即if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1)
更新满足条件点的距离,即将上一个点走过的距离加上 1。先到终点的为最小值
即d[x][y]=d[t.first][t.second]+1;
再将满足条件的点入队, 用于继续判断。
即q[++tt]=new PII(x,y);
注:这里需要运用到PII类
作用1:获取x(行数)、y(列数),用于上下左右移动+判断
作用2:将该点入队
即q[++tt]= new PII(x,y);
最后直接返回距离即可
即return d[n-1][m-1];(注意数组下标从0开始)
手动模拟

注:BFS类似于一颗二叉树
保证每一层往外扩,距离逐渐增加(入队出队)

注:到达交叉口的位置,将可走的点入队,再依次出队。
出队的每个点拿出来判断,如果下一个点可走,则将下一个点进入到队列尾中。
这样入队出队的操作保证了一层一层往外扩,并且搜索到的每一层的距离相等。
如搜索到第一层,为距离为1的点,第二层,为距离为2的点,依此类推。
上下左右
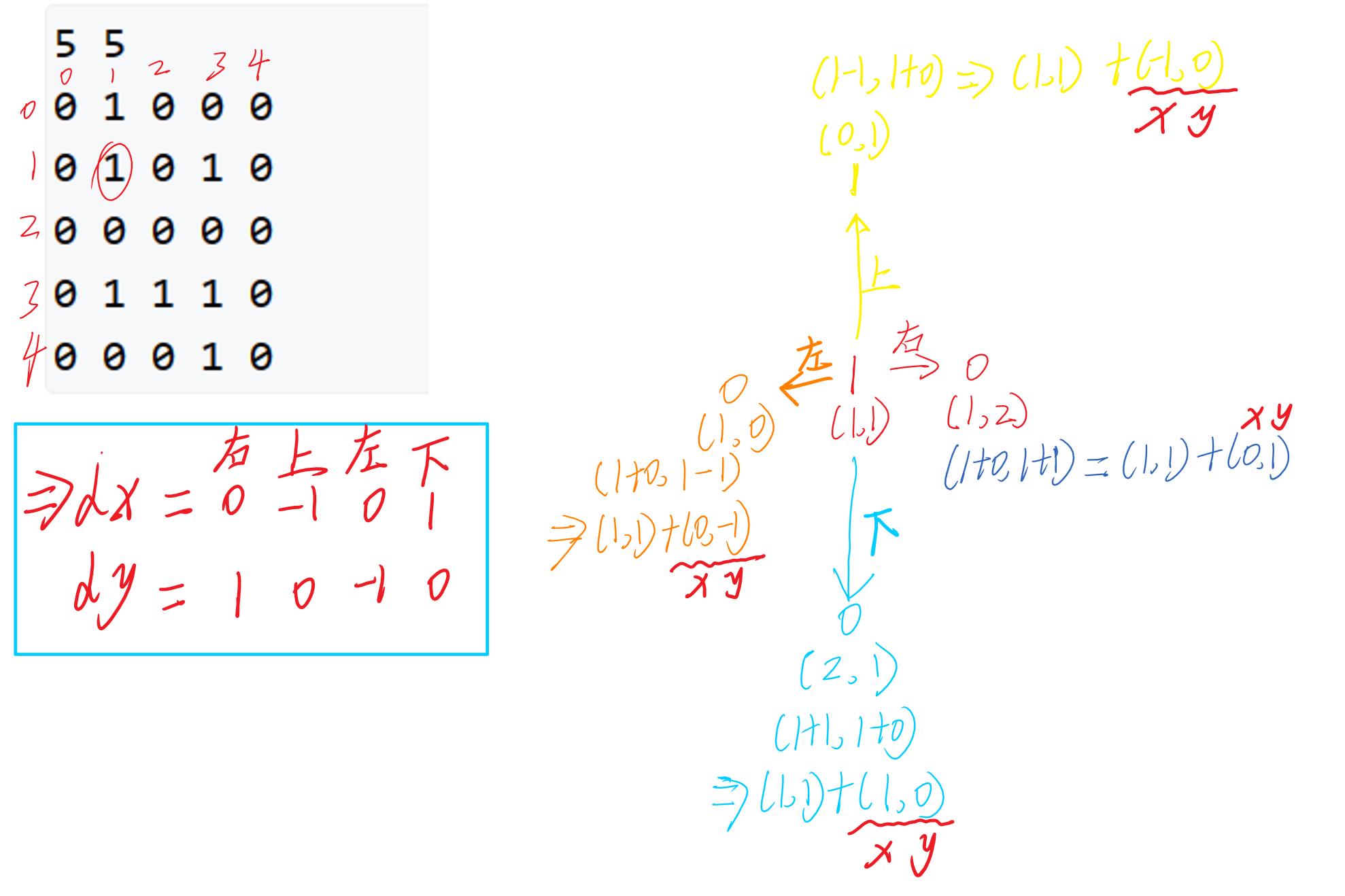
代码
import java.io.*;
public class Main{
static int N=110,hh,tt,n,m;
//N数据为100,多开10个单位,防止越界。
static int [][]g=new int[N][N];
static int [][]d=new int[N][N];
static PII []q=new PII[N*N];
//最多移动整个数组,即N行N列
public static int bfs() {
hh=0;//初始化队头
tt=-1;//初始化队尾
d[0][0]=0;//第0行第0列为入口
q[++tt]=new PII(0,0);//往队尾添加第一个点
int dx[]= {-1,0,1,0};
int dy[]= {0,1,0,-1};
/*
向上移动:
dx[0]=-1 dy[0]=0 (-1,0) 列不变,行数往上移
向右移动:
dx[1]=0 dy[1]=1 (0,1) 行不变,列数往右移
向下移动:
dx[2]=1 dy[2]=0 (1,0) 列不变,行数往下移
向左移动:
dx[3]=0 dy[3]=-1 (0,-1) 行不变,列数往左移
*/
while(hh<=tt) {
PII t=q[hh++];//取出队头
for(int i=0;i<4;i++) {
//向上、下、左、右移动
int x = t.first+dx[i];
int y = t.second+dy[i];
/*同时满足以下条件:
(1)x,y大于等于0并且x<n,y<m不越界
(2)走到的点为0,不为1,
(3)走到的位置还没被走过
*/
if(x>=0&&x<n&&y>=0&&y<m&&g[x][y]==0&&d[x][y]==-1) {
d[x][y]=d[t.first][t.second]+1;//满足条件,则在原来走过的距离上加一,记录走过的距离。
q[++tt]=new PII(x,y);//再将该点(x,y)插入到队尾,用于下面的判断。
}
}
}
return d[n-1][m-1];//返回从起点到终点的距离,数组下标从0开始,即n-1,m-1
}
public static void main(String []args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
//BufferedWriter out = new BufferedWriter(new OutputStreamWriter(System.out));
String []s = in.readLine().split(" ");
n = Integer.parseInt(s[0]);
m=Integer.parseInt(s[1]);
for(int i=0;i<n;i++) {
String []st = in.readLine().split(" ");
for(int j=0;j<m;j++) {
g[i][j]=Integer.parseInt(st[j]);//读入数据
d[i][j]=-1;//初始化每行每一列的位置,代表还没走过。
}
}
System.out.println(bfs());//输出数字
//out.write(bfs());输出数字对应的字符
//out.close();
}
}
class PII{//PII
int first,second;
public PII(int first,int second){//构造方法
this.first=first;
this.second=second;
}
}
八数码
二刷
分析
问题描述
给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
看到至少需要进行多少次交换,很容易就想到最短操作,最短步数,最短距离问题。
题目样例如下:

那么我们需要怎么做,才能将初始网格移动到最终网格?
做法
采用的是BFS+键值对映射的方法来做。
(1)输入格式为字符串
首先,需要将输入格式从传统的数组转为字符串,这样做的好处是便于匹配两串是否相等。
如果相等,输出最少操作步数,如果不等,则输出-1。
(2)一维下标<–>二维下标+交换
拿到一个初始串后,我们需要获取x在字符串中的下标k,通过k转换为对应二维数组的下标。
这样做的好处是便于控制上下左右方向偏移量
再将偏移后的数组下标又转为一维数组下标
这样做的好处是便于交换在字符串的两个字符
(3)Map键值对映射+队列
最后,通过Map键值对映射的方式,将入队的字符串记录距离,在之前的队头走过的距离加上1即可,将转换位置的字符串入队,进入新一轮的循环,再出队,继续bfs下一层,通过出队、入队的操作,确保一层一层往外搜,看是否能找到一个串和目标串匹配成功,先搜到的即为最短距离(步数)。可以的话,输出距离,否则,输出-1。
数组下标转换推导

注:数组是3*3的数组,每/3确保了有三个数是在同一行,%3(余数)是确定列数。
情况模拟

注:红色的代表的是往符合两串相等的方向走的,在实际过程中,每一块的x是按上下左右都走一遍,能走就入队,然后再出队,继续这个过程,bfs一层一层往下搜,直至找到与终串相同。
代码
import java.util.*;
public class Main{
public static void swap(char arr[],int x,int y){
char temp=arr[x];
arr[x]=arr[y];
arr[y]=temp;
}
public static int bfs(String start,String end){
Map<String,Integer>map=new HashMap<>();//键值对映射
Queue <String>q=new LinkedList<>();//队列
q.offer(start);//start入队
map.put(start,0);//将入队的第一个字符串映射成数值0
//上下左右移动
int dx[]={-1,0,1,0};
int dy[]={0,1,0,-1};
while(!q.isEmpty()){
String t=q.poll();//取出队头
int k=t.indexOf('x');//获取x在字符串中的下标
//一维数组下标转换为二维数组下标
int x=k/3;
int y=k%3;
if(t.equals(end))return map.get(t);//获取t走过的距离
for(int i=0;i<4;i++){
//上下左右移动
int a=x+dx[i];
int b=y+dy[i];
if(a<3&&a>=0&&b<3&&b>=0){
//转换为字符数组
char arr[]=t.toCharArray();
//二维数组下标转换为一维数组下标
//刚开始是/3,所以需要*3。接着是%3,就需要加上余数b。
swap(arr,k,a*3+b);
String str=new String(arr);//字符数组转换位字符串
if(map.get(str)==null){//如果map中无该字符串
map.put(str,map.get(t)+1);//在原来队头走过的距离加上1
q.offer(str);//再将字符串入队
}
}
}
}
return -1;//不匹配则输出-1
}
public static void main(String []args){
Scanner in = new Scanner(System.in);
String start="";
for(int i=0;i<9;i++){
String x=in.next();
start+=x;//字符串拼接
}
String end="12345678x";
System.out.println(bfs(start,end));
}
}
蓝桥经典真题:全球变暖
分析
其中”上下左右”四个方向上
#连在一起的一片陆地组成一座岛屿。
具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋.),它就会被淹没。
题目模拟(岛屿)
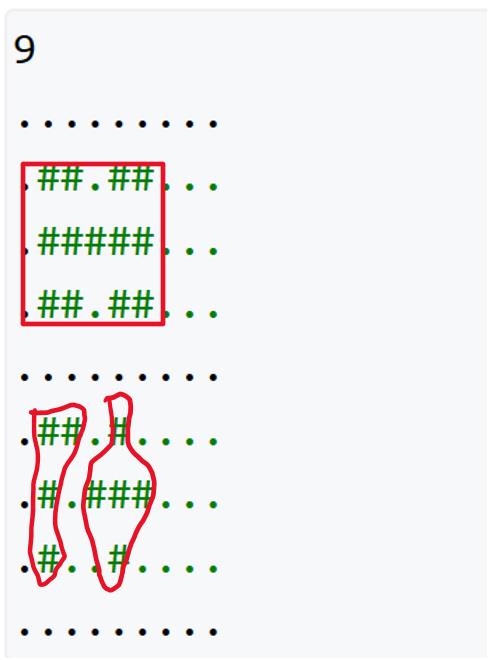
注:图中有3个岛屿,上下连续区域。
题目模拟(海洋淹没)

注:题中有一个岛屿全被淹没
题目解读
观察一下:岛屿中陆地的数量和海洋的数量是统一的。
如果这个陆地上下左右方向只要有一个方向有.的话,就说明该陆地会被淹没。
也就是只要我们在陆地上下左右方向中找到了一个.,就说明这个陆地被淹没。
换言之,如果说岛屿中陆地被淹没了,就存在至少一个方向的海洋.。
我们只需要统计岛屿的个数和海洋的个数即可。
如果海洋个数和岛屿中陆地的个数相等,则说明该岛屿已被淹没。否则未被淹没。
所以,关键在于维护海洋和岛屿中陆地的个数。
这题用BFS来处理
首先没有点与点之间的关系,所以我们不用邻接表来存储边和点的关系。
而是用队列的方式去维护BFS一层一层往外搜,一层一层往外扩。
那在bfs中我们还需要维护其他变量用于解决此题。
首先,我们需要去统计连通块(岛屿)中陆地的个数 res。
这里在队头元素出队的时候,统计一下即可。
设定isbound来标记是边界的.
然后,弹出队头,进行上下左右的坐标移动,统计其上下左右方向是否有.。
有的话,我们就将该位置的坐标标记上false。
最后统计一下每个岛屿的isbound的个数有多少个。
如果说res和isbound相等,则说明该岛屿全部淹没。
代码
import java.util.*;
public class Main{
static int N=1010;
static char g[][]=new char[N][N];
static boolean st[][]=new boolean [N][N];
static int dx[]= {1,0,-1,0};
static int dy[]= {0,-1,0,1};
static int n;
static int cnt;
public static void main(String []args) {
Scanner in=new Scanner(System.in);
n=in.nextInt();
for(int i=0;i<n;i++) {
char a[]=in.next().toCharArray();
for(int j=0;j<n;j++) {
g[i][j]=a[j];
}
}
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++) {
if(g[i][j]=='#'&&!st[i][j]) {
if(bfs(i,j))cnt++;
}
}
}
System.out.println(cnt);
}
public static boolean bfs(int x,int y) {
Queue<pair>q=new LinkedList<>();
q.add(new pair(x,y));
int res=0;
int bound=0;
st[x][y]=true;
while(!q.isEmpty()) {
pair t=q.poll();
res++;
boolean isbound=false;
for(int i=0;i<4;i++) {
int a=t.x+dx[i];
int b=t.y+dy[i];
if(a<0||a>=n||b<0||b>=n)continue;
if(st[a][b])continue;
if(g[a][b]=='.') {
isbound=true;
continue;
}
q.add(new pair(a, b));
st[a][b]=true;
}
if(isbound)bound++;
}
return res==bound;
}
}
class pair{
int x;
int y;
public pair(int x,int y) {
this.x=x;
this.y=y;
}
}
微博转发(每日一题)
ACcode
import java.util.*;
public class Main{
static int N=100010;
static int n,m;
static int idx=0;
static int e[]=new int [N];
static int ne[]=new int [N];
static int h[]=new int [N];
static boolean []st=new boolean[N];
public static void add(int a,int b){
e[idx]=b;
ne[idx]=h[a];
h[a]=idx++;
}
public static int dfs(int start){
int res=0;
int cnt=0;
LinkedList<Integer>list=new LinkedList<>();
Arrays.fill(st,false);
st[start]=true;
list.add(start);
int len=list.size();
while(!list.isEmpty()){
int t=list.removeFirst();
len--;
for(int i=h[t];i!=-1;i=ne[i]){
int j=e[i];
if(!st[j]){
st[j]=true;
list.add(j);
res++;
}
}
if(len==0){
cnt++;
len=list.size();
}
if(cnt==m)break;
}
return res;
}
public static void main(String []args){
Scanner in=new Scanner(System.in);
n=in.nextInt();
m=in.nextInt();
Arrays.fill(h,-1);
for(int i=1;i<=n;i++){
int a=in.nextInt();
for(int j=0;j<a;j++){
int b=in.nextInt();
add(b,i);
}
}
int q=in.nextInt();
while(q-->0){
int x=in.nextInt();
System.out.println(dfs(x));
}
}
}
![]()
![]()
![]()
看在寸铁这么肝的份上,不妨点个关注 ![]()


后续有好的题目会放在这里,明天更新图的遍历+最短路!!!
记得复习前面背过的模板,考前反复是致胜前提!!!