第四期：DFS(暴搜)

蓝桥杯热门考点模板总结来啦 ~

你绝绝绝绝绝绝对不能错过的常考DFS模板

冲刺蓝桥杯省一模板大全来啦 ~

蓝桥杯4月8号就要开始了 ~

距离蓝桥杯省赛倒数第5天

还不清楚DFS(暴搜)的同学快快看过来

还没背熟模板的伙伴们背起来

真题千千万万遍，蓝桥省一自然现！

祝大家4月8号蓝桥杯上岸 ~

不清楚蓝桥杯考什么的点点下方

考点秘籍

蓝桥杯竞赛干货

算法竞赛字符串常用操作总结！！！

往期回顾

蓝桥杯上岸每日N题第一期(一)！！！

蓝桥杯上岸每日N题第一期(二)！！！

蓝桥杯上岸每日N题第一期(三)！！！

蓝桥杯上岸每日N题第二期(一)！！！

蓝桥杯上岸每日N题第三期(一)！！！

蓝桥杯上岸必刷专题

蓝桥杯上岸必刷！！！(日期专题+保姆级教学)

蓝桥杯上岸必刷！！！(字符串专题)

蓝桥杯上岸必刷！！！(模拟/枚举专题)

想背纯享模版的伙伴们点点下方

蓝桥杯省一你一定不能错过的模板大全(第一期)

蓝桥杯省一你一定不能错过的模板大全（第二期）

想背注释模版的伙伴们点点下方

蓝桥杯必背第一期

蓝桥杯必背第二期

蓝桥杯上岸必背！！！ (第三期 DP)

想看JavaB组填空题的伙伴们点点下方

填空题

DFS/BFS是蓝桥杯的热门考点,距离省赛仅剩5天,干就完事了

下面让我们开始刷起来

DFS你的大脑，BFS你的体力

让我们一起上岸蓝桥杯

DFS

排列数字 (经典模型)

从前往后填数字，保证后面填的数字和前面不冲突。

需要两个数组：

path[]：记录走过的路径

st[]:标记该路是否被走过

(1)运用DFS搜索+回溯遍历整个二叉树
(2)当走到最后一个点时，输出结果,同时回退到上一层，即return。
(3) (2)操作执行完后回溯到上一层,判断上一层的数是否被标记过
若已标记过，则不再更换,再回溯到上一层。
没有标记过，则需要进行更换，再继续dfs()下去，依次类推，直至回溯到根节点。
待整颗树都遍历完，则退出循环。

分析图

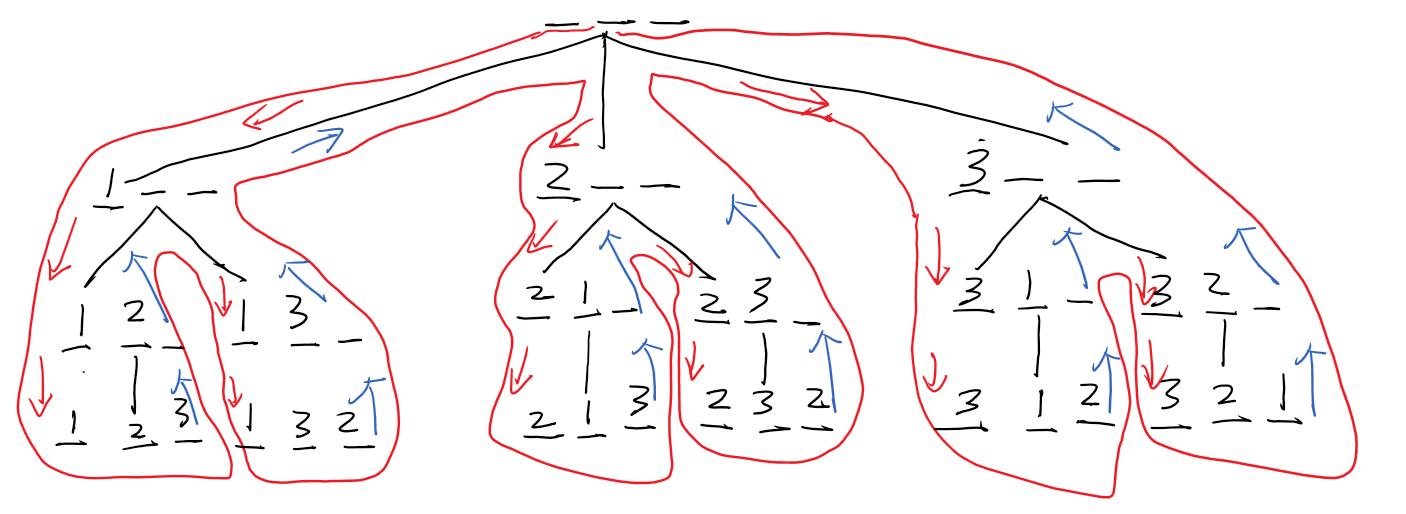
注：蓝色上升箭头表示回溯方向

代码剖析

return;
表示的是返回到上一层，用于回溯，可有可无，推荐加上，便于理解。
st[i]=false;//恢复现场+回溯
(1)依次将最后一个数标记为false,可以将该数拿来重新用，空出了位置,即为恢复现场。
(2)表示的是在走到最后一个数，再无路可走时,将最后一个数标记为false,表示可以重新用该数进行回溯，结合return，回溯到上一层。
再进行判断是否该数在这一层未被标记，若未标记则可以替换,再dfs下一层。若被标记过，则继续回溯到上一层。依次类推，直至回溯到根节点位置。
其他代码请见注释

代码

//暴搜
import java.util.Scanner;
public class Main{
    static int N=10;
    static int n,u;//n表示总层数，u表示当前在第几层
    static int []path = new int [N];//记录走过的路径
    static boolean []st=new boolean[N];//标记数组
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();//总共有n层

        dfs(0);//从根节点0开始dfs递归
    }
    public static void dfs(int u){
        if(u==n){
        //走到第n层，此时无路可走，输出结果。

            for(int i=0;i<n;i++) System.out.print(path[i]+" ");
            System.out.println();//每到n个换行

            return;
            //返回到上一层，如u=2,返回到上一层为1的位置;
        }

        else{
            for(int i=1;i<=n;i++){//从i=1开始，到n结束。
                if(!st[i]){//该数未被标记
                    path[u]=i;
                    //如果i在这一轮循环中的这一层未被标记，则将放在这个位置

                    st[i]=true;//标记路已走过了，不能再走，避免冲突。

                    dfs(u+1);//进入下一层

                    st[i]=false;
                    //将最后一个数设置为未标记，恢复现场，回溯。
                }
            }
        }
    }
}

n-皇后问题(经典模型)

对角线推断 ！！！

引言：DFS搜索的方法很多，确保搜索的顺序清楚是关键！

第一种方法(回溯)

任意两个皇后都不能处于同一行、同一列或同一斜线上。
同一行：DFS的u从行开始搜索，不需要额外维护一个数组。
同一列：维护一个col[]数组，标记同一行被用过的位置。
同一斜线：
<1>正对角线：
维护dg[]数组，标记正对角线被用过的位置。
<2>反对角线：
维护udg[]数组，标记反对角线被用过的位置
只有同时满足这三个条件,即col[]、dg[]、udg[]均未被标记,才能放置皇后。
在递归的过程中，先满足条件的先放置，回溯过程再去寻找每一层另外满足条件的位置。

分析

运用DFS+回溯摆放皇后的位置

DFS放皇后的位置：
如果col[]、dg[]、udg[]均未被标记,则满足条件,才能够放置皇后。
即if(!col[i]&&!dg[u+i]&&!udg[n-u+i])

放置完皇后后，需要将col[]、dg[]、udg[]标记为true，表示已经用过不能再使用。
即col[i]=dg[u+i]=udg[n-u+i]=true;

再一层一层往下搜索：dfs(u+1)

恢复现场+回溯：
return: 回溯到上一层,再进行判断，直至回溯到第一层。

再将col[]、dg[]、udg[]标记为false，表示恢复现场，可以拿出来回溯判断。
即col[i]=dg[u+i]=udg[n-u+i]=false;

最后将回溯过程中皇后不满足的位置设为 .
即g[u][i]='.';

手动模拟

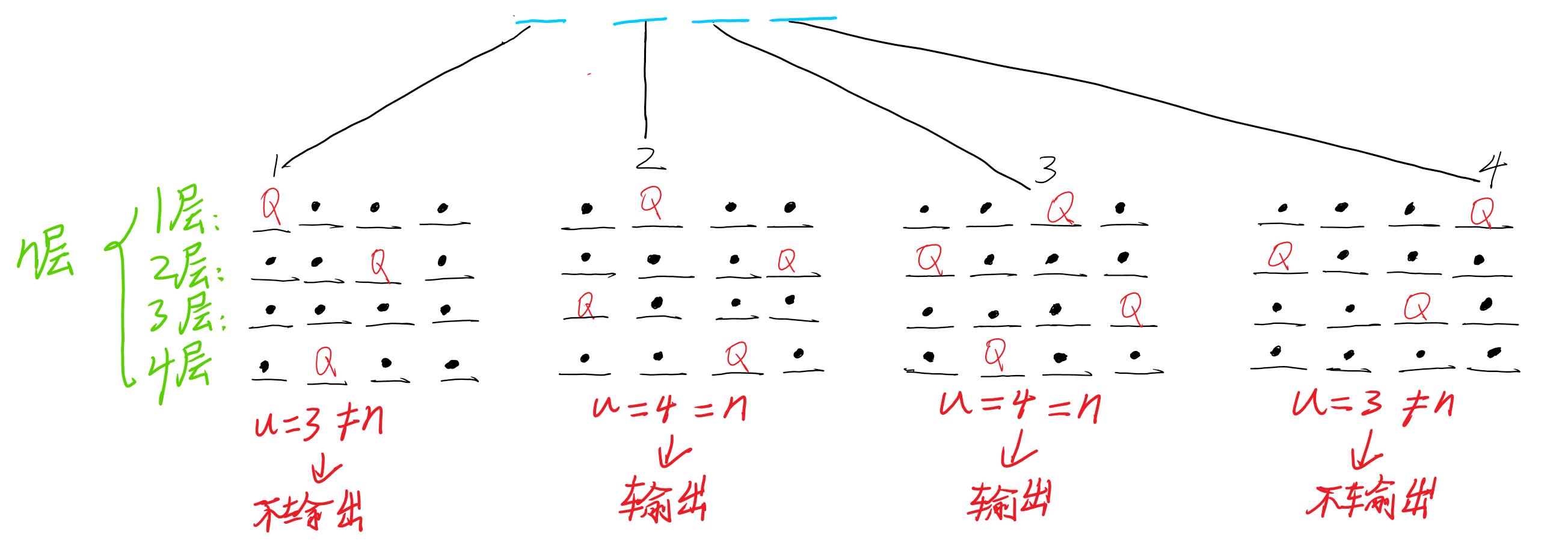
注：每一行只会有一个皇后，依次枚举皇后应该放置的位置，存在无解情况

以i=2为例（模拟走位）

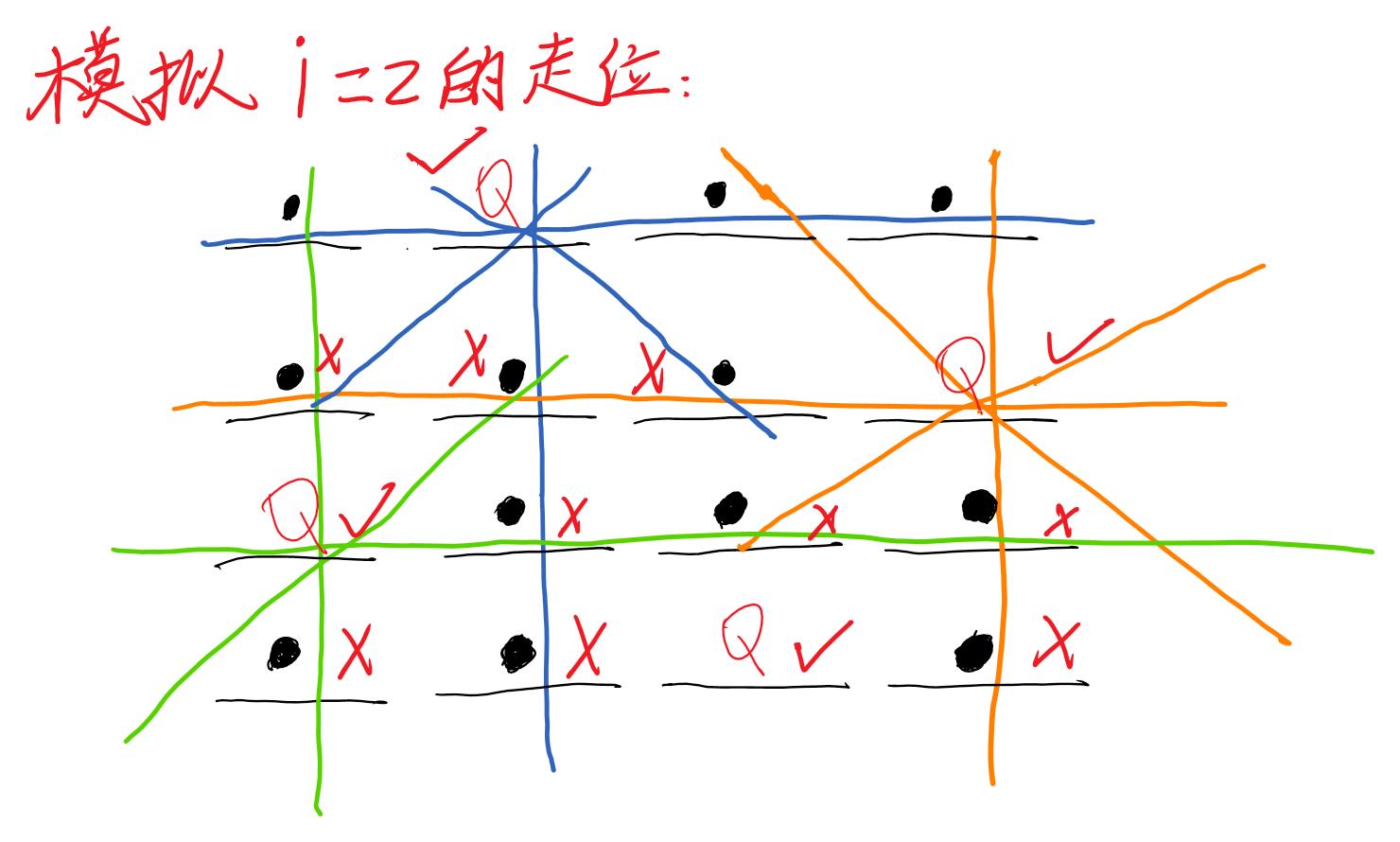
注：不同的颜色的划线表示每个位置的列、正对角线、反对角线的位置（点）
x 表示不能放置皇后，√ 表示可以放置皇后

以i=2为例（模拟回溯）

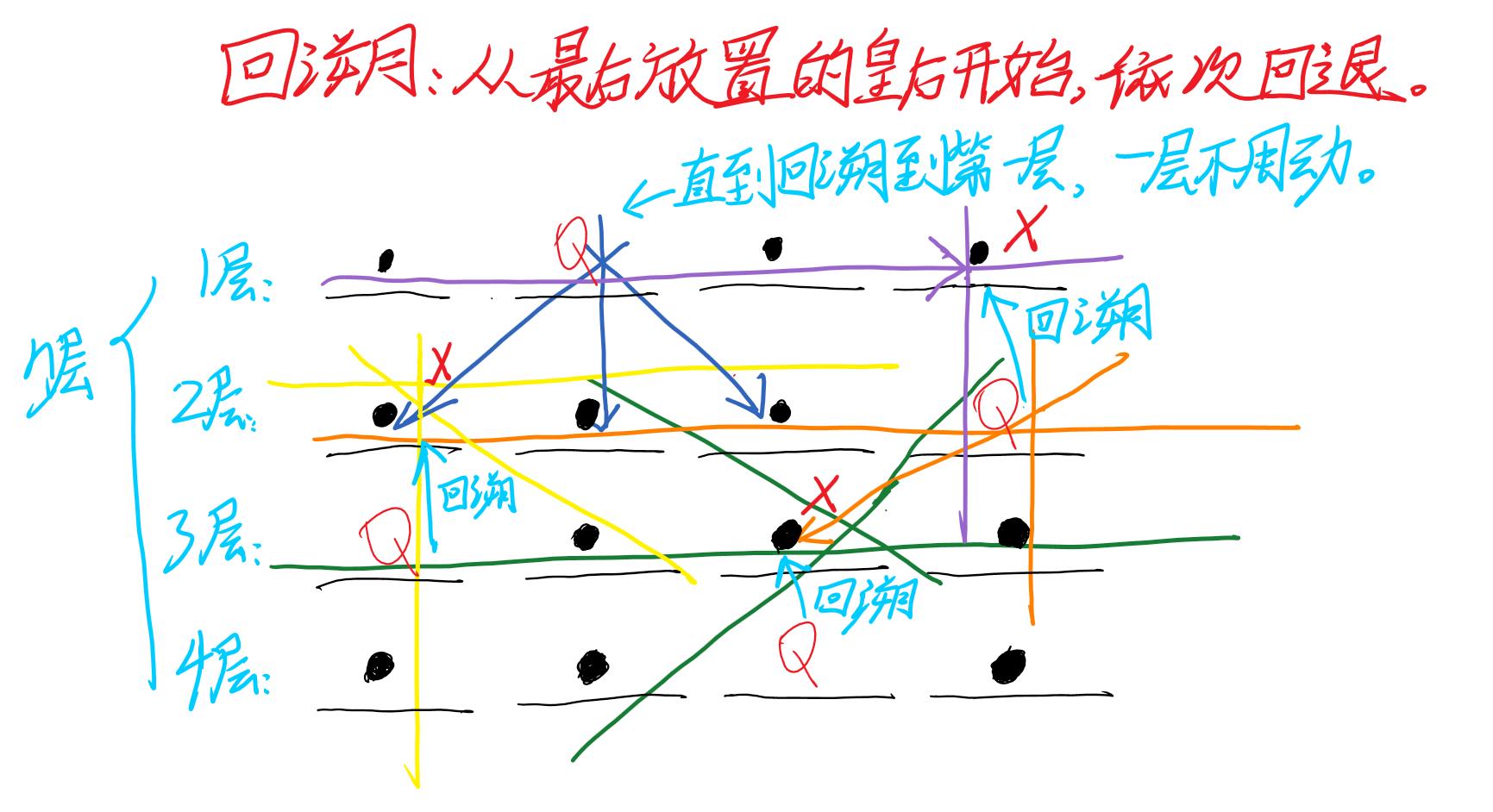
dg、udg公式推导

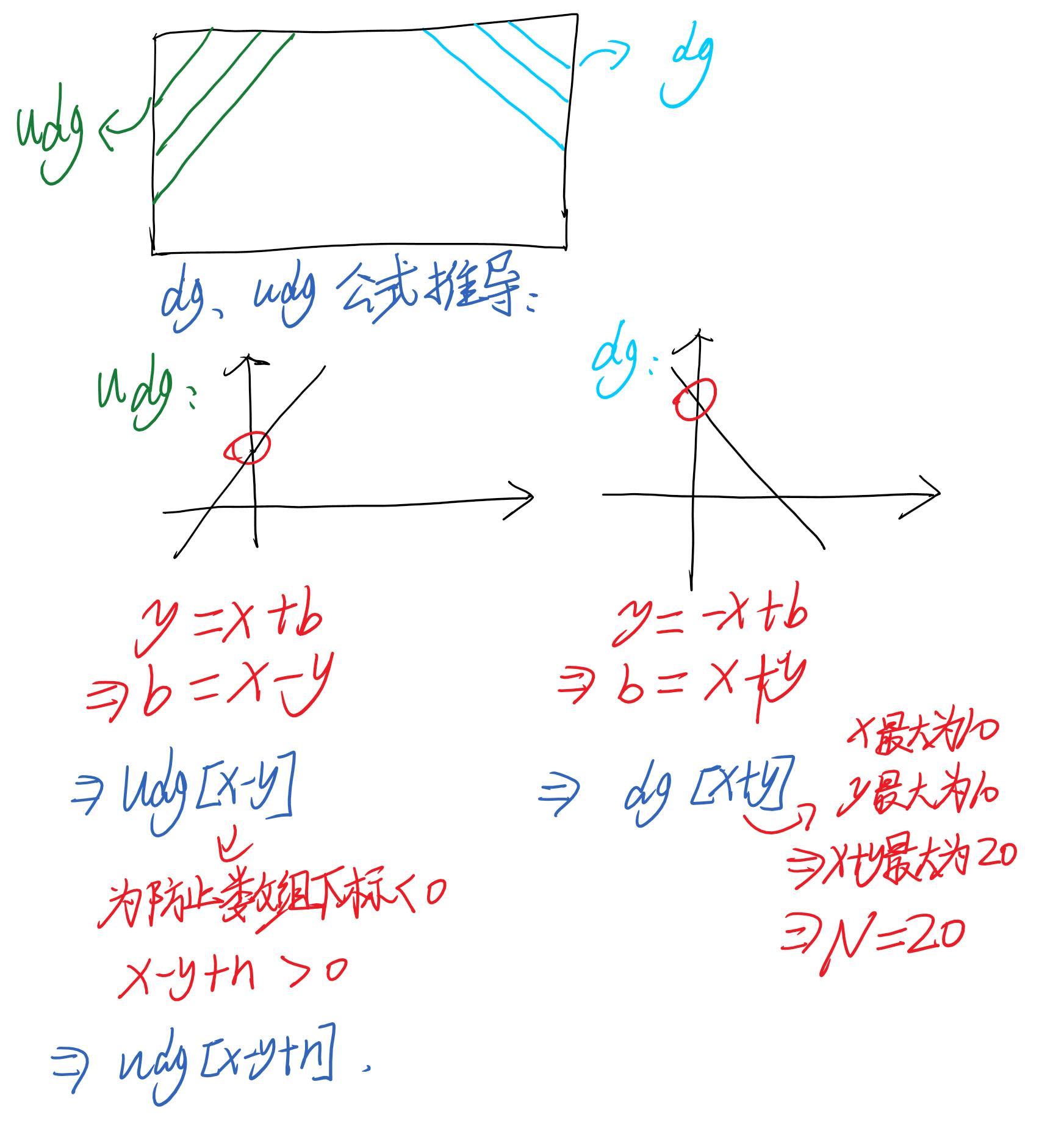
代码

import java.util.*;
public class Main{
    static int N=20;
    static int n;
    static char[][]g = new char[N][N];///模拟棋盘数组
    static boolean []col = new boolean[N];//列
    static boolean []dg = new boolean[N];//正对角线
    static boolean []udg=new boolean[N];//反对角线
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n = in.nextInt();

       // int n = in.nextInt();
       //局部变量如果重新定义，则使用全局变量,造成无输出。

        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g[i][j]='.';
                //先把棋盘上每个位置 初始化为 . 
            }
        }
        dfs(0);
        //从第0层开始搜索
    }
    public static void dfs(int u){

        if(u==n){//n个皇后都放置好了
            for(int i=0;i<n;i++){
                for(int j=0;j<n;j++){
                    System.out.print(g[i][j]);
                }
                System.out.println();
            }
            System.out.println(); //其他方案数换行
            return; //返回到上一层
        }
        for(int i = 0;i<n;i++){ //i表示的是列数，u表示的是行数

            if(!col[i]&&!dg[u+i]&&!udg[n-u+i])//严格满足列、正对角线、反对角线之前均无放置(标记)过
            {

            g[u][i]='Q';//满足条件的放Q，即皇马的位置
            col[i]=dg[u+i]=udg[n-u+i]=true;//标记满足条件的皇马位置
            dfs(u+1);//继续递归处理下一层

            //将最后放置的皇后位置设置为false，返回上一层，开始回溯。
            //将其列、正对角线和反对角线都设置为false，表示这些位置可以重新模拟，搜索满足条件的位置。
            //再进行递归下一层。
            //回溯的那层，放置的皇后严格满足列、正对角线、反对角线之前均无放置过，否则不能放置于此。
            //如果均未被标记，则将皇后放置于此，否则不满足，置为 . 
             col[i]=dg[u+i]=udg[n-u+i]=false;


            g[u][i]='.';
            //初始化的g[u][i]='.'是先将棋盘所有的点设为 . 
            //为什么这里还需要再写g[u][i]='.';
            //是因为回溯过程中，会模拟皇后走过的位置。
            //如果没有加上这一句，输出方案显示的是到头+回溯过程中皇马模拟走过的所有位置。
            //所以需要加上这一句，将回溯过程中皇后不满足的位置设为 .
        }
        }
    }
}

第二种方法(依次枚举每个位置)

时间复杂度：O(n*n)
注：与第一种方法的区别：
第一种方法是精炼后的枚举：每一行只能有一个皇后。
重点在于搜索(枚举)的顺序

分析

(1)依次枚举每个位置，放是一个分支，不放也是一个分支。
如不放皇后里面有不放和放的情况，依次枚举各个位置，输出满足的方案。

(2)row[] 数组
由于第一种方法是确定每一行是只有一个皇后，所以不需要多维护一个row[] 行 数组
但是第二种方法是依次枚举每个位置，需要多维护一个row[] 行 数组,记录行的位置。

模拟图

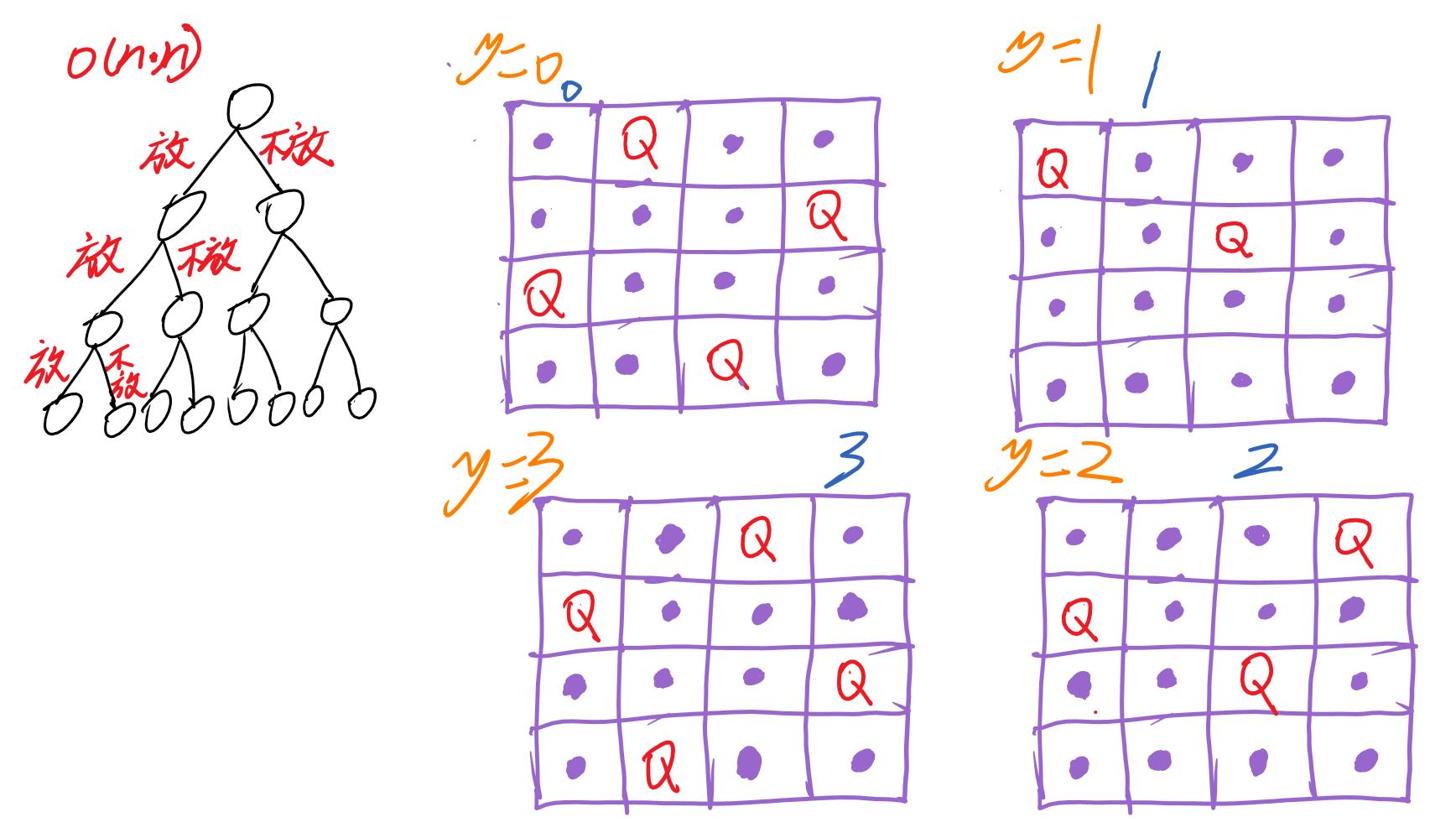
假设从第一层的第0列枚举到第3列，如图所示，再往下一层走，依次类推
注：依次枚举每个位置，分为放和不放，根据条件放置皇后，当然会标记已走过的，用于判断放不放皇后。再置为false，用于枚举时重新判断。

代码

import java.util.*;
public class Main{
    static int N=10;
    static char g[][]=new char[N][N];
    static boolean dg[]=new boolean[2*N];
    static boolean udg[]=new boolean[2*N];
    static boolean col[]=new boolean[N];
    static boolean row[]=new boolean[N]; 
    static int n;
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n=in.nextInt();

        //初始化方式(1)
        /*for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
                g[i][j]='.';
            }
        }
        */

        dfs(0,0,0);
    }
    //x表示行数，y表示列数,s记录放置了的皇后的数量
    public static void dfs(int x,int y,int s){

        if(s>n)return;//超过就返回

        //如果列数到了第n列，需要将列数拔回到第0列，同时往下一行(层)
        if(y==n)
        {y=0;//列数拔回到第0列
        x++;//往下一行(层)
        }

        if(x==n){//走到第n层
            if(s==n){//如果放置了的皇后的数量等于n，则输出
            for(int i=0;i<n;i++){
            for(int j=0;j<n;j++){
            System.out.print(g[i][j]);

        }
           System.out.println();
        }
            System.out.println();//每一种方案换行
        }
        return;//必加
        }
    //初始化方式(2)    
    g[x][y]='.';//初始化每个点为 . 

    //不放皇后，直接走到下一列
    dfs(x,y+1,s);

    //放皇后
    if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[n+x-y]){
        g[x][y]='Q';//放置皇后

        //放置过皇后，剩余的方案不能选该位置。
        row[x]=col[y]=dg[x+y]=udg[n+x-y]=true;

        dfs(x,y+1,s+1);
        //往下一列走，每放置了皇后，s就加一，用于输出判断

        //恢复现场，留待剩余方案的皇后位置的放置
        row[x]=col[y]=dg[x+y]=udg[n+x-y]=false;

        g[x][y]='.';//不满足的设为.
    }

}
}

小猫爬山

分析

要尽可能减少花费-->递归的分支尽可能少-->优先考虑放重猫
优先考虑放重猫，需要从大到小排个序，
一直往下搜索，答案是唯一的。
放得下猫就继续往该车往下加
放不下就再另外开一辆放猫
分两个分支去放
开一辆继续放其他猫的为一个分支
开另一辆单独只放一只猫的为另一个分支
接下来递归调用处理，对于每个分支递归后有又n个分支，一直递归下去，直至递归到n层。说明当前的车数为最优解。
我们可以建立如下递归搜索图：

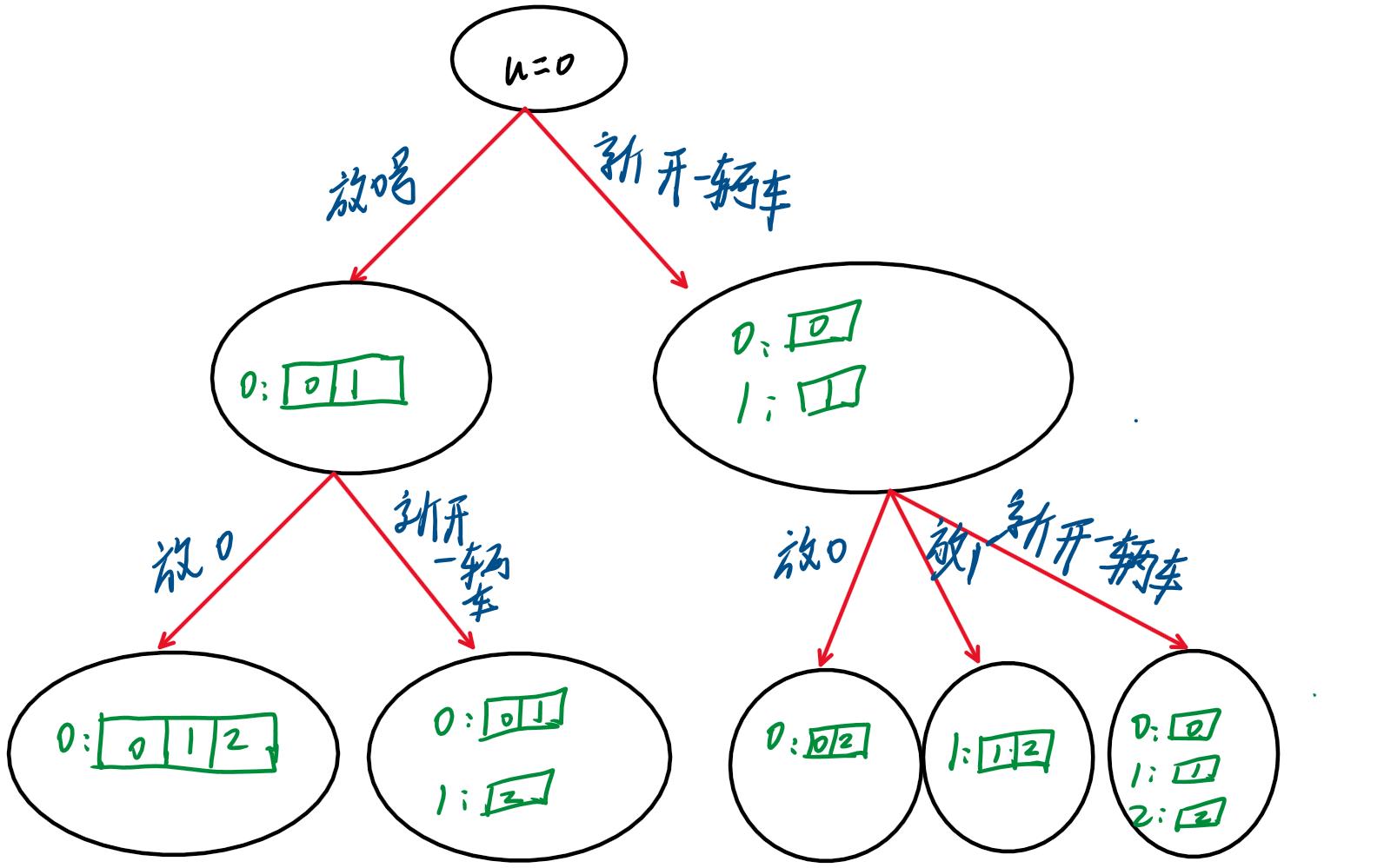
DFS小结：

递归DFS最简单直接的理解方式就是按照你的做题逻辑顺序来写
所以做题的逻辑顺序至关重要，确保不重不漏地确保方案。
按逻辑写出来可以跑得动即可，不要过分地去深究内在实现，会很纠结。
注意dfs下一层要恢复现场，这是必需的。
深究不外乎：递归下一层+置false回溯上一层用+去掉无用的分支剪枝

Accode

//从大到小排个序，优先放重猫。
//一直往下搜索，答案是唯一的。
//放得下猫就继续往下加
//放不下就再另外开一辆，继续放
//分两个分支去放
//开一辆继续放其他猫的有一个分支
//开另一辆只放一只猫的也有一个分支
import java.util.*;
public class Main{
    static int N=20;
    static int n,m;
    static int arr[]=new int [N];
    static int ans=N;
    static int car[]=new int [N];
    static int cat[]=new int[N];
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n=in.nextInt();
        m=in.nextInt();
        for(int i=0;i<n;i++)cat[i]=in.nextInt();
        Arrays.sort(arr,0,n);
        //从小到大排个序
        Reverse(arr,0,n-1);
        //再从大到小排个序，优先放重猫
        dfs(0,0);
        System.out.println(ans);
    }
    //直接把他看成是第一遍模拟，剩下的递归处理即可。
    public static void dfs(int u,int k){
        if(k>=ans)return;
        if(u==n){
            //走到n时，即为找到答案ans=当前小车的数量k
            ans=k;
            return;
        }
        //考虑猫都放一辆车的情况
        for(int i=0;i<k;i++){
            if(cat[u]+car[i]<=m){
                car[i]+=cat[u];
                dfs(u+1,k);
                car[i]-=cat[u];
                //恢复现场,便于下一次加猫操作
            }
        }
        //考虑猫只放一辆车的情况
        car[k]=cat[u];
        dfs(u+1,k+1);
        //每次dfs会用到一辆车，所以需要加一。
        car[k]=0;
        //恢复现场
    }
    public static void Reverse(int q[],int l,int r)
    //反转函数 -->从大到小排个序
    {
        for(int i=l,j=r;i<j;i++,j--){
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
        }
    }

}

不同路径数

分析

关键句：走过的位置可以重复走
看到题目，我们可以发现每个任意的位置都可以往上下左右四个方向任意走。
再看到输出样例，发现走了k次后，得到的是不重复的k位组合数(k从0开始)。
我们可以建立如下暴力搜索树：

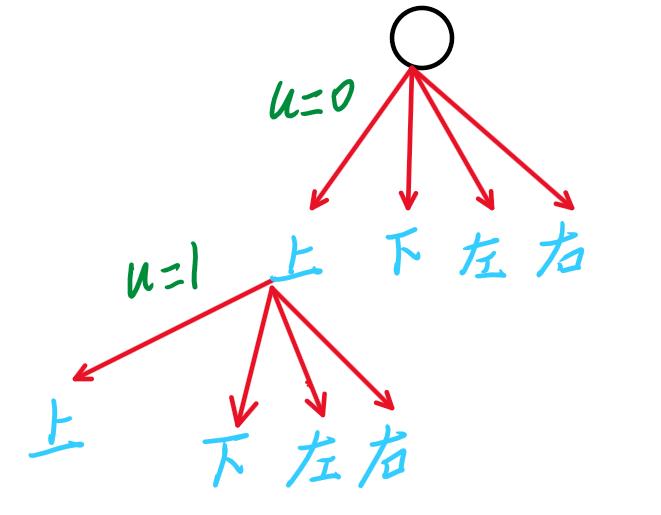
我们可以暴力搜索每个位置，每个位置都往上下左右方向走k步即可。
再将走了k步的数字保存到set中,这样我们得到的是不重不漏的组合数。
再把输出set.size()即可。

时间复杂度

n,m,k最大都为5
554^k*10=256000=O(2 x10^5)
是可以过的，可以不用快读快写，但是像BFS、DFS这些题目比赛时快读快写比较稳。

小结

DFS通常与递归结合使用,从某个起点出发,限制操作次数。
走到终点时进行相应的记录或者操作。
一条路走到黑,暴力枚举结合递归各个方向或者操作。
像本题：
dfs(int x,int y,int u,int sum);
注：通常从起点0开始
满足条件的再递归下一层(下一个点)
dfs(x, y,u+1, sum);

ACcode(下标从0开始推荐)

//暴搜--->递归搜索树
//往上下左右四个方向走
import java.util.*;
public class Main{
    static int N=10;
    static int arr[][]=new int [N][N];
    static int dx[]={0,1,-1,0};
    static int dy[]={1,0,0,-1};
    static int n,m,k;
    static Set<Integer>set=new HashSet<>();
    //存的是每次走过的距离
    //不出现重复的距离
    public static void main(String []args){

        Scanner in =new Scanner(System.in);
         n=in.nextInt();
         m=in.nextInt();
         k=in.nextInt();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                arr[i][j]=in.nextInt();
                 //bfs(i,j,0,arr[i][j]);
            }
        }
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                bfs(i,j,0,arr[i][j]);
                //从i ,j 出发,u标记走的步数
            }
        }

        System.out.println(set.size());
    }
    public static void dfs(int x,int y,int u,int num){
        //确定边界
        if(u==k)set.add(num);
        else{
            //直接暴搜，四个方向都走一便，u走到k时将走过的距离存进set中。
            for(int i=0;i<4;i++){
            int a=x+dx[i];
            int b=y+dy[i];
            if(a>=0&&a<n&&b>=0&&b<m){
                //在范围内都可以走
                //秦九韶算法
                dfs(a,b,u+1,num*10+arr[a][b]);
            }
            }
       //return set.size(); 
    }
}
}

Accode2(下标从1开始)

import java.util.*;
public class Main{
    static int N=10;
    static int n,m,k;
    static int arr[][]=new int [N][N];
    static int dx[]={0,0,-1,0,1};
    static int dy[]={0,1,0,-1,0};
    static Set<Integer>set=new HashSet<>();
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n=in.nextInt();
        m=in.nextInt();
        k=in.nextInt();
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                arr[i][j]=in.nextInt();
            }
        }
        int u=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=m;j++){
                dfs(i,j,1,arr[i][j]);
            }

        }
        System.out.println(set.size());

    }
    public static void dfs(int x,int y,int u,int num){
        if(u==k+1)set.add(num);
        else{
            for(int i=1;i<=4;i++){
                int a=x+dx[i];
                int b=y+dy[i];
                if(a>=1&&a<=n&&b>=1&&b<=m){
                    dfs(a,b,u+1,10*num+arr[a][b]);
                }
            }
        }
    }
}

快读快写版

import java.util.*;
import java.io.*;
public class Main{
    static int N=10;
    static int n,m,k;
    static int arr[][]=new int [N][N];
    static int dx[]={0,-1,0,1};
    static int dy[]={1,0,-1,0};
    static Set<Integer>set=new HashSet<>();
    public static void main(String []args)throws IOException{
       // Scanner in = new Scanner(System.in);
    BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
    PrintWriter pw=new PrintWriter(new OutputStreamWriter(System.out));
    String str[]=bf.readLine().split(" ");
        n=Integer.parseInt(str[0]);
        m=Integer.parseInt(str[1]);
        k=Integer.parseInt(str[2]);
        for(int i=0;i<n;i++){
            String s[]=bf.readLine().split(" ");
            for(int j=0;j<m;j++){
                arr[i][j]=Integer.parseInt(s[j]);
            }
        }
        int u=0;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                dfs(i,j,0,arr[i][j]);
            }

        }
      pw.println(set.size());
      pw.flush();
    }
    public static void dfs(int x,int y,int u,int num){
        if(u==k)set.add(num);
        else{
            for(int i=0;i<4;i++){
                int a=x+dx[i];
                int b=y+dy[i];
                if(a>=0&&a<n&&b>=0&&b<m){
                    dfs(a,b,u+1,10*num+arr[a][b]);
                }
            }
        }
    }
}

带分数（蓝桥真题）

分析

说明：
先递归枚举a，枚举的每个a表示一种方案,a中再递归枚举c。
最后判断一下b是否满足等式并且每个位置上的数是否不重复。
统计输出方案，再将方案总数输出即可。

秦九韶算法：

数：abc
ab=a*10+b;
abc=ab*10+c;
例如 123
1*10+2=12;
12*10+3=123;

注意：

java数组拷贝：

Arrays.copyOf();

含义：方法复制指定的数组，截断或用零填充（如有必要），因此副本具有指定的长度。 对于在原始数组和副本中都有效的所有索引，这两个数组将包含相同的值。

例如：
a[]=new *[];
b[]=new int[];
Arrays.copyOf(a,b);
说明：复制两个数组：前一个为任意类型*，后一个必须为整形。

Object.clone();

含义：创建并返回此对象的副本。
详见：https://www.runoob.com/manual/jdk11api/java.base/java/lang/Object.html#clone()
a[]=new *[];
b[]=new *[];
b=a.clone();
复制各种类型像：boolean、int等等
前提是数组类型必须一 一对应：
如a是int型,则b也必须为int型。
a是boolean型,则b也必须为boolean型

小结：常用的是Arrays.sort()拷贝两个整型数组。
涉及到除int相同类型外的数组拷贝用clone()较好。

Accode

import java.util.*;
public class Main{
    static int N=10;
    static int n,ans;
    static boolean st[]=new boolean[N];
    static boolean backup[]=new boolean[N];
    public static void main(String  []args) {
        Scanner scan=new Scanner(System.in);
        n=scan.nextInt();
        dfs_a(0,0);
        //u表示用了多少个数，也就是枚举的层数
        //a表示当前枚举的数字
        System.out.println(ans);    
    }
    public static boolean check(int a,int c) {
        long b=n*(long)c-a*c;
        //算出b值
        if(a==0||b==0||c==0)return false;

        backup=st.clone();
        //备份数组，便于后续的使用。
        while(b>0) {
            int x=(int) (b%10);
            b/=10;
            if(x==0||backup[x])return false;
            //枚举时对数字进行标记，数字不能重复出现。
            //不含前导0
            backup[x]=true;
        }
        for(int i=1;i<=9;i++) {
            if(!backup[i])return false;
        //如果全部数字没有用到返回false;

        }
        return true;
        //满足的方案
    }
    public static void dfs_c(int u,int a,int c) {
        if(u>9)return;
        //c分支最多枚举9层,大于9层则说明不满足。
        if(check(a, c))ans++;
        //检查一下a,c看是否满足条件
        //记录满足的方案数

        for(int i=1;i<=9;i++) {
            if(!st[i]) {
                st[i]=true;
                dfs_c(u+1, a, c*10+i);
                //秦九韶算法
                st[i]=false;
                //恢复现场
                //你用完了就需要恢复成原来的样子
                //下次别人才可以继续用

            }

        }
    }
    public static void dfs_a(int u,int a) {
        //u表示用了多少个数
        if(a>=n)return;
        //如果a大于或等于目标值n，则说明不满足直接return;
        //return表示终止退出
        if(a>0)dfs_c(u,a,0);
        //对于每个枚举的a值，都有c的分支

        for(int i=1;i<=9;i++) {
            if(!st[i]) {
                st[i]=true;
                dfs_a(u+1, a*10+i);
                //枚举下一层，秦九韶算法
                st[i]=false;
                //恢复现场
            }
        }
    }
}

小猫爬山

分析

要尽可能减少花费-->递归的分支尽可能少-->优先考虑放重猫
优先考虑放重猫，需要从大到小排个序，
一直往下搜索，答案是唯一的。
放得下猫就继续往该车往下加
放不下就再另外开一辆放猫
分两个分支去放
开一辆继续放其他猫的为一个分支
开另一辆单独只放一只猫的为另一个分支
接下来递归调用处理，对于每个分支递归后有又n个分支，一直递归下去，直至递归到n层。说明当前的车数为最优解。
我们可以建立如下递归搜索图：

DFS小结：

递归DFS最简单直接的理解方式就是按照你的做题逻辑顺序来写
所以做题的逻辑顺序至关重要，确保不重不漏地确保方案。
按逻辑写出来可以跑得动即可，不要过分地去深究内在实现，会很纠结。
注意dfs下一层要恢复现场，这是必需的。
深究不外乎：递归下一层+置false回溯上一层用+去掉无用的分支剪枝

Accode

//从大到小排个序，优先放重猫。
//一直往下搜索，答案是唯一的。
//放得下猫就继续往下加
//放不下就再另外开一辆，继续放
//分两个分支去放
//开一辆继续放其他猫的有一个分支
//开另一辆只放一只猫的也有一个分支
import java.util.*;
public class Main{
    static int N=20;
    static int n,m;
    static int arr[]=new int [N];
    static int ans=N;
    static int car[]=new int [N];
    static int cat[]=new int[N];
    public static void main(String []args){
        Scanner in = new Scanner(System.in);
        n=in.nextInt();
        m=in.nextInt();
        for(int i=0;i<n;i++)cat[i]=in.nextInt();
        Arrays.sort(arr,0,n);
        //从小到大排个序
        Reverse(arr,0,n-1);
        //再从大到小排个序，优先放重猫
        dfs(0,0);
        System.out.println(ans);
    }
    //直接把他看成是第一遍模拟，剩下的递归处理即可。
    public static void dfs(int u,int k){
        if(k>=ans)return;
        if(u==n){
            //走到n时，即为找到答案ans=当前小车的数量k
            ans=k;
            return;
        }
        //考虑猫都放一辆车的情况
        for(int i=0;i<k;i++){
            if(cat[u]+car[i]<=m){
                car[i]+=cat[u];
                dfs(u+1,k);
                car[i]-=cat[u];
                //恢复现场,便于下一次加猫操作
            }
        }
        //考虑猫只放一辆车的情况
        car[k]=cat[u];
        dfs(u+1,k+1);
        //每次dfs会用到一辆车，所以需要加一。
        car[k]=0;
        //恢复现场
    }
    public static void Reverse(int q[],int l,int r)
    //反转函数 -->从大到小排个序
    {
        for(int i=l,j=r;i<j;i++,j--){
        int temp=arr[i];
        arr[i]=arr[j];
        arr[j]=temp;
        }
    }

}

看到这里，不妨点个关注