平衡树的分类
- treap (BST + heap(大根堆))
- 红黑树
- splay
- sbt
- AVL
BST(二叉搜索树)
- 定义
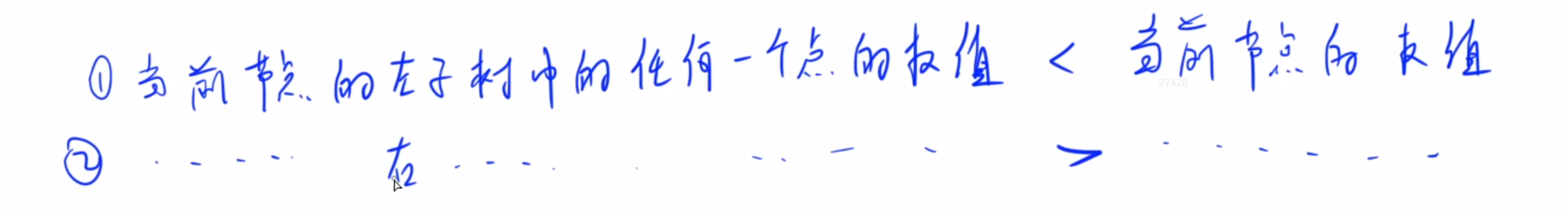
- 性质
- BST的中序遍历一定是一个递增序列, 一个树的中序遍历就是将一颗树的各个节点投影到叶子节点的水平面上的序列.
- 任何随机一棵BST的期望(平均)高度为logn, 这里我们用大根堆的随机权值来达到随机的目的.
- 应用场景
动态维护一个有序序列.
Treap
定义: 中序遍历满足严格递增且满足大根堆的树.
-
Treap和BST的基本操作
- 插入
- 删除
- 前驱,后继: I. 前驱: 一直沿着当前节点的左子树的右儿子走(最大值)直到某个点没有右儿子, 则该点为前驱, II. 后继: 一直沿着当前节点的左子树的左儿子走直到某个点没有左儿子, 则该点为后继(最小值)
- 求某个数的在平衡树中的序号
- 求序号为k的数
- 求比某个值大的最小节点的值(这个值不一定在平衡树里面)
- 求比某个值小的最大节点的值
-
节点信息
struct node
{
int l, r; // 左右节点的编号
int key, value; // BST和heap的关键字 也就是说**treap的节点受到了两个数据结构特性的限制**
}trp;
-
空间复杂度 $O(n)$
对于线段树来说, 一个点是对应多个数, 所以空间复杂度为$O(4n)$的, 但是平衡树是每个点对应一个数, 所以空间复杂度就为$O(n)$. -
操作详解
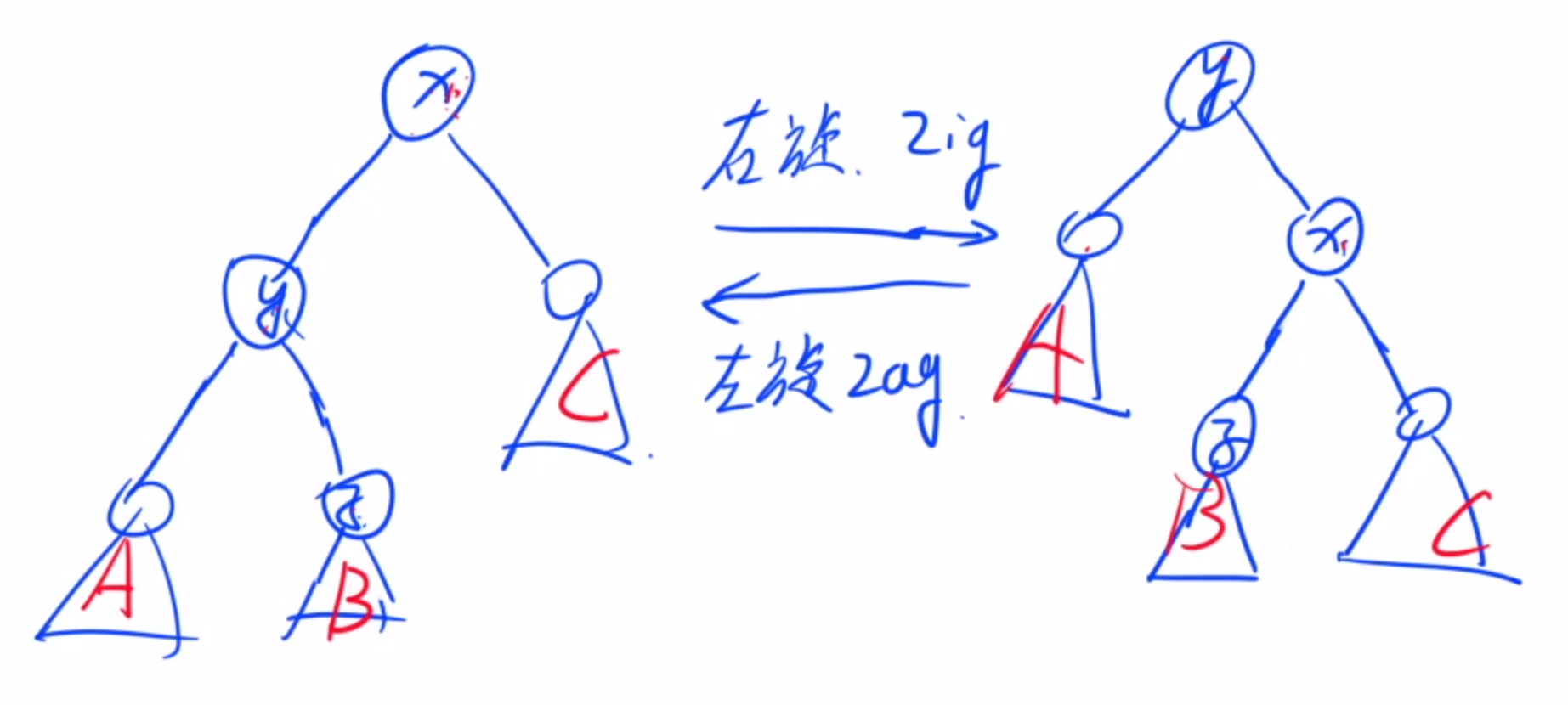
- 插入
左(zag)右(zig)旋 -> 不影响中序遍历
用途: 就是交换儿子节点与父节点
-
删除
不断左/右旋, 直到旋转到叶子节点, 直接擦除即可.
-
时间复杂度: $O(logn)$


优秀