题目描述

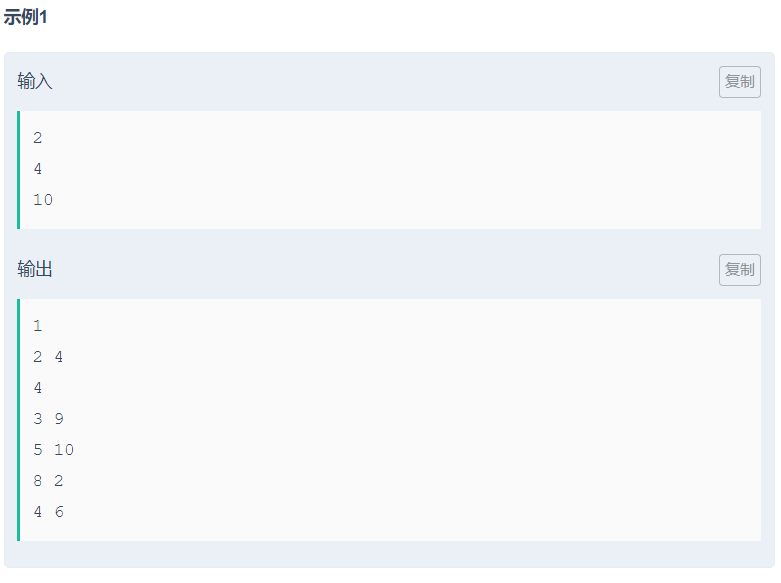
样例

·

问题分析

由题意可知，要构造 gcd(x,y)>1 ，显然与1无关，故不考虑1.
设 S(p) 为 2~n 所有最小质因子为p的数的集合
由上述定义，可将 2~n 中的所有整数划分到对应的集合中

例如 n = 10
S(2) = {2, 4, 6, 8, 10}
S(3) = {3, 9}
S(5) = {5}
S(7) = {7}

情况一：S(p).size() % 2 == 0

对于 ∀p, ∀x,y∈S(p), gcd(x,y) >= p && p > 1
那么，在同一个集合中即可任选两个数匹配进行构造，即可解决的 S(p).size() % 2 == 0 情况

情况二：S(p).size() % 2 == 1

若集合 S(p).size() % 2 == 1 时，要考虑到两个集合进行构造
设p1，p2，满足 S(p1).size() % 2 == 1 && S(p2).size() % 2 == 1 && p1 < p2
那么，可以选择 x = p1 * p2, y = p2，这样就能解决此问题
但是还是存有漏洞，万一 p1 > sqrt(n) 则 p1 * p2 > n，显然会出错
我们可以将所有 p ≤ sqrt(n) 的集合用上述方法处理，所有 p > sqrt(n) 的集合选择 x = p, y = 2 * p 处理
(当然你得判断y合法,)

实现方法

先用线性筛预处理出每个数的最小质因子，然后放入对应的集合 divv 中
优先构造 p > sqrt(n) 的情况
再处理 S(p).size() % 2 == 1的情况
最后将所有集合里的元素匹配即可

C++ 代码

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N = 2e5 + 10;

int p[N], tot, d[N], st[N];
void init(int n)//用线性筛预处理出每个数的最小质因子
{
    for (int i = 2; i <= n; i++)
    {
        if (!st[i]) p[++tot] = i, d[i] = i;
        for (int j = 1; j <= tot && i * p[j] <= n; j++)
        {
            st[i * p[j]] = 1;
            if (i % p[j] == 0)
            {
                d[i * p[j]] = d[i];
                break;
            }
            else d[i * p[j]] = p[j];
        }
    }
}

int t, n;
set<int>divv[N];

int main()
{
    init(200005);

    scanf("%d", &t);
    while (t--)
    {
        scanf("%d", &n);

        //放入对应的集合 divv 
        for (int i = 1; i <= n; i++) divv[i].clear();
        for (int i = 1; i <= n; i++) divv[d[i]].insert(i);

        //记录答案
        vector<int>a, b;
        a.clear(); b.clear();

        //优先构造 p > sqrt(n) 的情况
        int sqn = sqrt(n);
        int pos = upper_bound(p + 1, p + tot + 1, sqn) - p;
        for (int i = pos; p[i] <= n; i++)
        {
            int val1 = p[i], val2 = 2 * p[i];
            if (val2 > n) continue;
            a.push_back(val2);
            b.push_back(val1);
            divv[2].erase(val2);
            divv[p[i]].erase(val1);
        }

        //处理 S(p).size() % 2 == 1的情况
        vector<int>v;
        for (int i = 1; p[i] <= n; i++)
        {
            int sz = divv[p[i]].size();
            if (sz & 1) v.push_back(p[i]);
        }
        for (int i = 0; i + 1 < v.size(); i += 2)
        {
            int val1 = v[i], val2 = v[i + 1];
            if (1LL * val1 * val2 > n) continue;
            a.push_back(val1 * val2);
            b.push_back(val2);
            divv[val1].erase(val1 * val2);
            divv[val2].erase(val2);
        }

        //若存在奇数个元素的集合，直接删一个，以便后续处理
        for (int i = 1; p[i] <= n; i++)
        {
            if (divv[p[i]].size() % 2 == 1)
                divv[p[i]].erase(p[i]);
        }

        //最后将所有集合里的元素匹配
        for (int i = 1; p[i] <= n; i++)
        {
            for (auto it = divv[p[i]].begin(); it != divv[p[i]].end(); it++)
            {
                a.push_back(*it);
                it++;
                b.push_back(*it);
            }
        }

        printf("%d\n", a.size());
        for (int i = 0; i < a.size(); i++)
            printf("%d %d\n", a[i], b[i]);
    }
}

附

本人不太会写博客，若有错误，敬请指出，有点丑见谅