树上1维成本01背包

题目链接：Acwing

不太寻常的难题，才能让人在思考的过程中理解模型的本质
——HanX

关于树上背包

• 普通背包：任意排序后，i对前i-1有依赖（状态转移方程），形成依赖图，按照拓扑序推进
• 树上背包：依赖已经由题面确定（u对u的子树有依赖），按照拓扑序推进

到达目标节点的拓扑序[递推]，就是从目标节点进入的后序遍历序[递归]

关于memo和dpTable

memo比dptable可以少算一些状态（eg. 1维01背包最后一行）
memo是必然可以实现的，如果依赖图拓扑序的可以划分成规整的阶段，则daTable也可以实现
如果状态的某个维度不规整怎么办？在该维度上用dfs （本题就是如此）

若依赖图拓扑序的可以完全划分成规整的阶段，则速成线性DP

题目分析

看到题目，自然想套用01背包问题的解法：

状态与状态值

$f[u][j]: 以u为根的物品中，拼出重量小于等于j的方案中，最大价值$

转移方程

$f[u][j]= \max\limits_{\sum_i j_{child_i}= j}\left\{p[u] + \sum_i f[child_i][j_{child_i}] \right\}$
出问题了，这里$j_{child_i}$的分配自由度太高，循环导致复杂度太高

重新抽象状态

将以u为根的物品中，分为[1+u的子树个数]组，1(u自身)必选的前提下，拼出重量小于等于j的方案

Ref
Bilibili: 有依赖的背包（背包类树形dp）
Bilibili: 树形DP入门：树上背包问题
labuladong: 动态规划系列之最优子结构

关于DP状态设计的一点心得：

1. 附加状态可以避免状态转移出现分支(eg.Painting House)
2. 附加状态可以减少循环【空间换时间】(eg.有依赖的背包问题)，本质是因为状态粒度不够小的时候，对应的状态值没有办法重用。
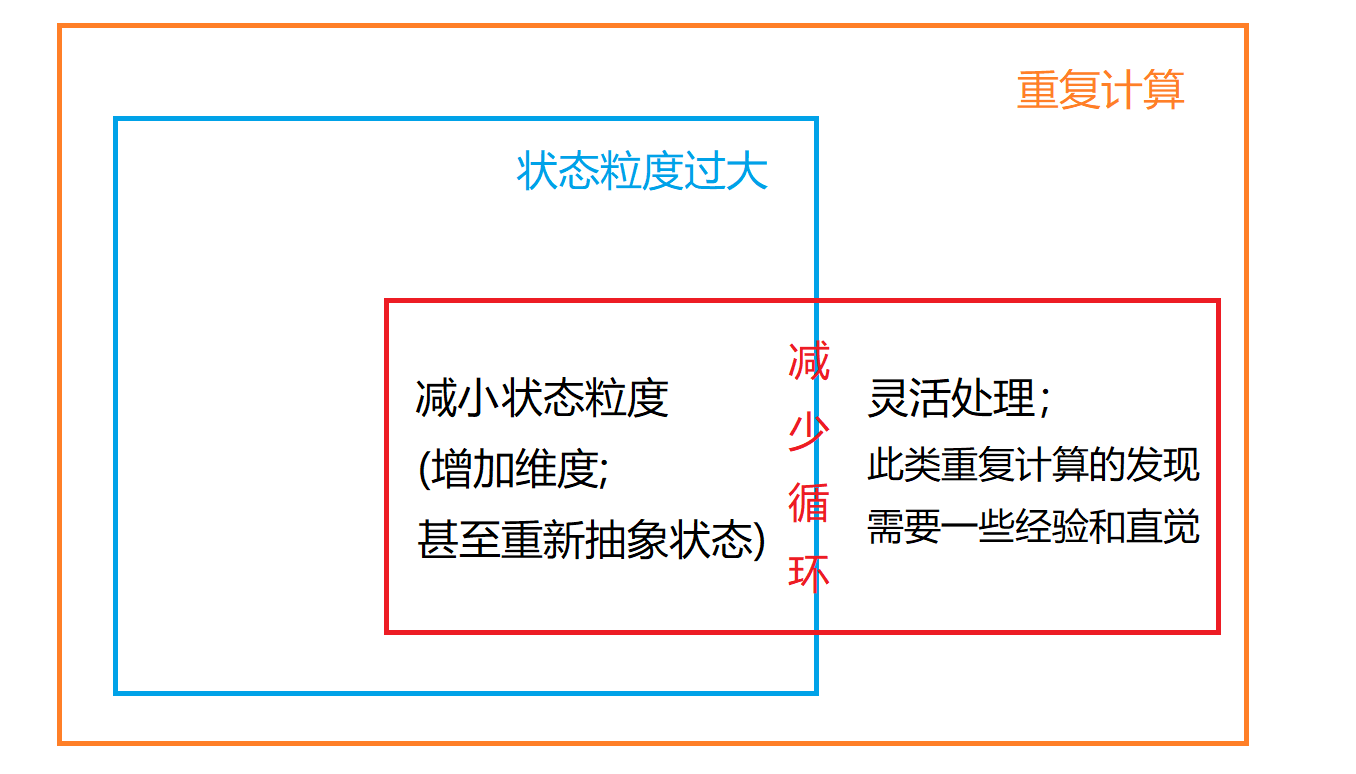
3. 但不是所有的循环都可以通过增加状态的方式减少【a.有些循环减少不了(没有重复计算)；b.可以减少的循环也有其他途径(完全背包)】。减少循环的必要条件是有重复计算，状态粒度过大是导致重复计算的原因之一（关系如下图）
   

DP的难点和魅力，都来自于状态的抽象的非套路性/艺术性

动态规划的艺术在于状态设计和子结构的挖掘。多年来，学界探讨了诸多DP转移的方法和优化手段，然而如何把问题形式化为状态空间，进一步抽象出DP的状态表示和阶段划分，往往是一件考查智力而非套路的事情。本章努力尝试把读者领进大门，但DP的这一难点仍然需要读者自己多加思考。练习设计DP算法并熟练使用它求解问题,也是提升读者在算法竞赛领域思维水平的一个重要途径。
——李煜东《算法竞赛进阶指南》

朴素解法

dfs

状态与状态值

$f[u][i][j] =$

$Case1: i\leq u子树个数时，$

$以u为根的物品组中，用前i个子树物品组，拼出重量小于等于j的方案中，最大价值，其中j\leq c-s[u]$

$Case2: i=u子树个数+1时，$

$以u为根的物品组中，用所有子树物品组，拼出重量小于等于j的方案中，最大价值，其中j\leq c$

转移方程

$f[u][i][j] = \max\limits_{1<=k<=j}\left\{f[u][i-1][j], f[u][i-1][j-k]+f[child_{i}][child_{i}子树个数+1][k]\right\}$

边界与初始值

$f[u][0][j] = 0$

Tip

会$TLE$

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N=105;
const int C=105;
int s[N], p[N];

struct Edge{
    int to;
};
vector<Edge> edge[N];

int dfs(int u, int i, int j){

    if(edge[u].size()-1==0){  //base case: 叶节点（无法选子树）
        if(s[u]<=j) return p[u];
        if(s[u]> j) return 0;
    }

    if(i==0){   //base case: 不选子树
        if(s[u]<=j) return p[u];
        if(s[u]> j) return 0;
    }

    //不选第i组物品
    int res = dfs(u, i-1, j); 
    //从第i组中选体积为k的物品
    int son = edge[u][i].to;   //每棵子树是一个物品组
    for(int k=1; k<=j-s[u] ; k++){   //泛化物品为体积
        res = max( res, dfs(u, i-1, j-k) + dfs(son, edge[son].size()-1, k) );
    }

    return res;
}

int main(){
    int n,c; cin>>n>>c;

    for(int i=1; i<=n; i++) edge[i].push_back({i}); //占位，为了保证第一个孩子的秩是1

    int root;
    for(int i=1; i<=n; i++){
        cin>>s[i]>>p[i];
        int fa; cin>>fa;

        if(fa==-1)  root = i;
        else        edge[fa].push_back({i});
    }

    cout<<dfs(root, edge[root].size()-1, c);

    return 0;
}

时间优化

dfs+memo

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N=105;
const int C=105;
int s[N], p[N];

struct Edge{
    int to;
};
vector<Edge> edge[N];

int f[N][N][C];
int dfs(int u, int i, int j){
    if(f[u][i][j]!=-1) return f[u][i][j];

    if(edge[u].size()-1==0){  //base case: 叶节点（无法选子树）
        if(s[u]<=j) return f[u][0][j]=p[u];
        if(s[u]> j) return f[u][0][j]=0;
    }

    if(i==0){   //base case: 不选子树
        if(s[u]<=j) return f[u][0][j]=p[u];
        if(s[u]> j) return f[u][0][j]=0;
    }

    //不选第i组物品
    int res = dfs(u, i-1, j); 
    //从第i组中选体积为k的物品
    int son = edge[u][i].to;   //每棵子树是一个物品组
    for(int k=1; k<=j-s[u] ; k++){   //泛化物品为体积
        res = max( res, dfs(u, i-1, j-k) + dfs(son, edge[son].size()-1, k) );
    }

    return f[u][i][j]=res;
}

int main(){
    int n,c; cin>>n>>c;

    for(int i=1; i<=n; i++) edge[i].push_back({i}); //占位，为了保证第一个孩子的秩是1

    int root;
    for(int i=1; i<=n; i++){
        cin>>s[i]>>p[i];
        int fa; cin>>fa;

        if(fa==-1)  root = i;
        else        edge[fa].push_back({i});
    }

    memset(f, -1, sizeof f);

    cout<<dfs(root, edge[root].size()-1, c);

    return 0;
}

递推(+dfs)+dpTable

有维度用到dfs是无奈之举，没有一个规整的递归拓扑序来让我们手动实现dpTable

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N=105;
const int C=105;
int n,c;
int s[N], p[N];

struct Edge{
    int to;
};
vector<Edge> edge[N];

int f[N][N][C];
void dfs(int u){    //Tip: 返回值为void
    //递归的base case: 叶节点（无法选子树）
    if(edge[u].size()-1==0){  // 有时，递归基的处理可以与非基情况合并，比如可以省略以下6行，但不建议
        for(int j=0; j<=c; j++){
            if(s[u]<=j)     f[u][1][j]=p[u];
            else if(s[u]>j) f[u][1][j]=0;
        }
        return;
    }

    //递归求解子问题
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to; //每棵子树是一个物品组, i==0时是指向自己
        dfs(son);  //填表        
    }

    //后序位置整合子问题的解
        //A. i==0时，分组背包的base case
    for(int j=0; j<=c-s[u]; j++){   //由于全局变量的初始值是0，故可省略以下2行，但不建议
        f[u][0][j]=0;   
    }
        //B. 1<=i<=[u子树个数]时，分组背包求解
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to;      //每棵子树是一个物品组, i==0时是指向自己

        for(int j=0; j<=c-s[u]; j++){ //a.体积已经约束过了
            f[u][i][j]=f[u][i-1][j];  //等价于k=0，代表第i组物品不选
            for(int k=1; k<=j; k++){  //泛化物品为体积, 从第i组中选体积为k的物品
                //b.这里的k不是j-s[u]，上面已经做过约束了
                f[u][i][j] = max( f[u][i][j], f[u][i-1][j-k] + f[son][edge[son].size()][k] );
            }
        }
    }
        //C. i==[u子树个数+1]时，分组背包求解
    for(int j=0; j<=c; j++){        
        if(j<s[u]){
            f[u][edge[u].size()][j]=0;
        }
        else if(s[u]<=j){
            f[u][edge[u].size()][j]=f[u][edge[u].size()-1][j-s[u]]+p[u];
        }
    }

}

int main(){
    cin>>n>>c;

    for(int i=1; i<=n; i++) edge[i].push_back({i}); //占位，为了保证第一个孩子的秩是1

    int root;
    for(int i=1; i<=n; i++){
        cin>>s[i]>>p[i];
        int fa; cin>>fa;

        if(fa==-1)  root = i;
        else        edge[fa].push_back({i});
    }

    dfs(root);
    cout<<f[root][edge[root].size()][c];

    return 0;
}

空间优化

滚动数组

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N=105;
const int C=105;
int n,c;
int s[N], p[N];

struct Edge{
    int to;
};
vector<Edge> edge[N];

int f[N][2][C];
void dfs(int u, int& lastPointer){
    int old, now=0; //每一次换行时更新
    //递归的base case: 叶节点（无法选子树）
    if(edge[u].size()-1==0){  // 有时，递归基的处理可以与非基情况合并，比如可以省略以下6行，但不建议
        old = now, now=1-old;
        for(int j=0; j<=c; j++){
            if(s[u]<=j)     f[u][now][j]=p[u];
            else if(s[u]>j) f[u][now][j]=0;
        }
        lastPointer = now;
        return;
    }

    //递归求解子问题
    vector<int> LPs; LPs.push_back(-1);
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to; //每棵子树是一个物品组, i==0时是指向自己
        int pointer;
        dfs(son, pointer);  //填表
        LPs.push_back(pointer);
    }

    //后序位置整合子问题的解
        //A. i==0时，分组背包的base case
    old = now, now=1-old;
    for(int j=0; j<=c-s[u]; j++){   //由于全局变量的初始值是0，故可省略以下2行，但不建议
        f[u][now][j]=0;   
    }
        //B. 1<=i<=[u子树个数]时，分组背包求解
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to;      //每棵子树是一个物品组, i==0时是指向自己

        old = now, now=1-old;
        for(int j=0; j<=c-s[u]; j++){ //a.体积已经约束过了
            f[u][now][j]=f[u][old][j];  //等价于k=0，代表第i组物品不选
            for(int k=1; k<=j; k++){  //泛化物品为体积, 从第i组中选体积为k的物品
                //b.这里的k不是j-s[u]，上面已经做过约束了
                f[u][now][j] = max( f[u][now][j], f[u][old][j-k] + f[son][LPs[i]][k] );
            }
        }
    }
        //C. i==[u子树个数+1]时，分组背包求解
    old = now, now=1-old;
    for(int j=0; j<=c; j++){        
        if(j<s[u]){
            f[u][now][j]=0;
        }
        else if(s[u]<=j){
            f[u][now][j]=f[u][old][j-s[u]]+p[u];
        }
    }

    lastPointer = now;
}

int main(){
    cin>>n>>c;

    for(int i=1; i<=n; i++) edge[i].push_back({i}); //占位，为了保证第一个孩子的秩是1

    int root;
    for(int i=1; i<=n; i++){
        cin>>s[i]>>p[i];
        int fa; cin>>fa;

        if(fa==-1)  root = i;
        else        edge[fa].push_back({i});
    }

    int pointer;
    dfs(root, pointer);
    cout<<f[root][pointer][c];

    return 0;
}

状态压缩

#include<iostream>
#include<cstring>
#include<vector>
using namespace std;

const int N=105;
const int C=105;
int n,c;
int s[N], p[N];

struct Edge{
    int to;
};
vector<Edge> edge[N];

int f[N][C];
void dfs(int u){
    //递归的base case: 叶节点（无法选子树）
    if(edge[u].size()-1==0){  // 有时，递归基的处理可以与非基情况合并，比如可以省略以下6行，但不建议
        for(int j=0; j<=c; j++){
            if(s[u]<=j)     f[u][j]=p[u];
            else if(s[u]>j) f[u][j]=0;
        }
        return;
    }

    //递归求解子问题
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to; //每棵子树是一个物品组, i==0时是指向自己
        dfs(son);  //填表
    }

    //后序位置整合子问题的解
        //A. i==0时，分组背包的base case
    for(int j=0; j<=c-s[u]; j++){   //由于全局变量的初始值是0，故可省略以下2行，但不建议
        f[u][j]=0;   
    }
        //B. 1<=i<=[u子树个数]时，分组背包求解
    for(int i=1; i<=edge[u].size()-1; i++){
        int son = edge[u][i].to;      //每棵子树是一个物品组, i==0时是指向自己

        for(int j=c-s[u]; j>=0; j--){ //a.体积已经约束过了
            for(int k=1; k<=j; k++){  //泛化物品为体积, 从第i组中选体积为k的物品
                //b.这里的k不是j-s[u]，上面已经做过约束了
                f[u][j] = max( f[u][j], f[u][j-k] + f[son][k] );
            }
        }
    }
        //C. i==[u子树个数+1]时，分组背包求解
    for(int j=c; j>=0; j--){        
        if(j<s[u]){
            f[u][j]=0;
        }
        else if(s[u]<=j){
            f[u][j]=f[u][j-s[u]]+p[u];
        }
    }

}

int main(){
    cin>>n>>c;

    for(int i=1; i<=n; i++) edge[i].push_back({i}); //占位，为了保证第一个孩子的秩是1

    int root;
    for(int i=1; i<=n; i++){
        cin>>s[i]>>p[i];
        int fa; cin>>fa;

        if(fa==-1)  root = i;
        else        edge[fa].push_back({i});
    }

    dfs(root);
    cout<<f[root][c];

    return 0;
}