线段树是算法竞赛中常用的用来维护 区间信息 的数据结构。

线段树可以在 $O(\log N)$ 的时间复杂度内实现单点修改、区间修改、区间查询（区间求和，求区间最大值，求区间最小值）等操作。

线段树这种数据结构可以很好的处理区间查询和区间修改的问题，虽然树状数组也可以通过差分的思想来实现区间修改，但是树状数组通常只能用于区间求和，而线段树能够处理区间最大值/最小值等一系列问题。

和分治思想很相像，线段树的每一个节点都储存着一段区间[L, R]的信息，其中叶子节点L=R。它的大致思想是：根据mid = l + r >> 1将一段大区间平均地划分成2个小区间[L, mid]和[mid + 1, R]，每一个小区间都再平均分成2个更小区间，以此类推，直到每一个区间的L等于R（这样这个区间仅包含一个节点的信息，无法被划分）。通过对这些区间进行修改、查询，来实现对大区间的修改、查询。

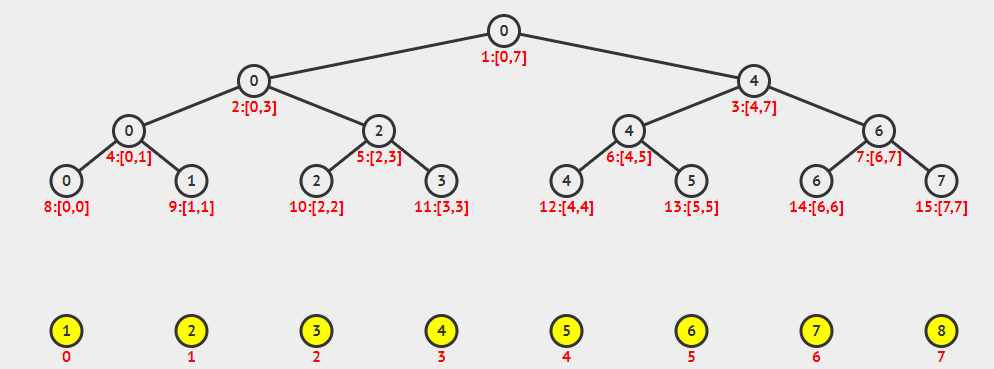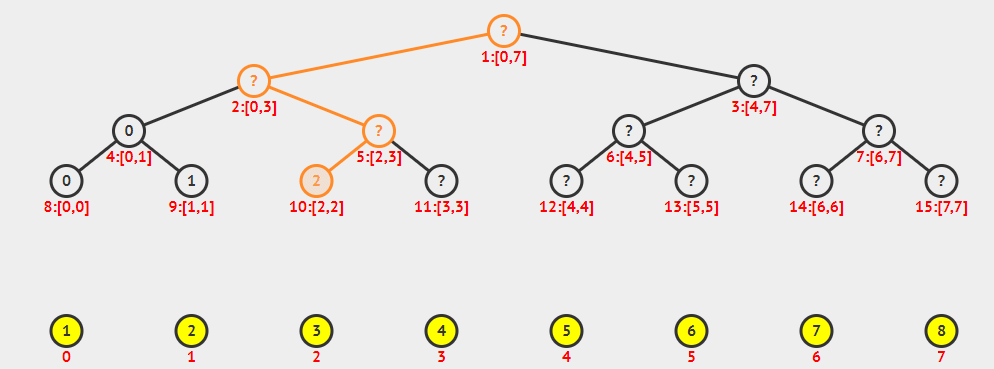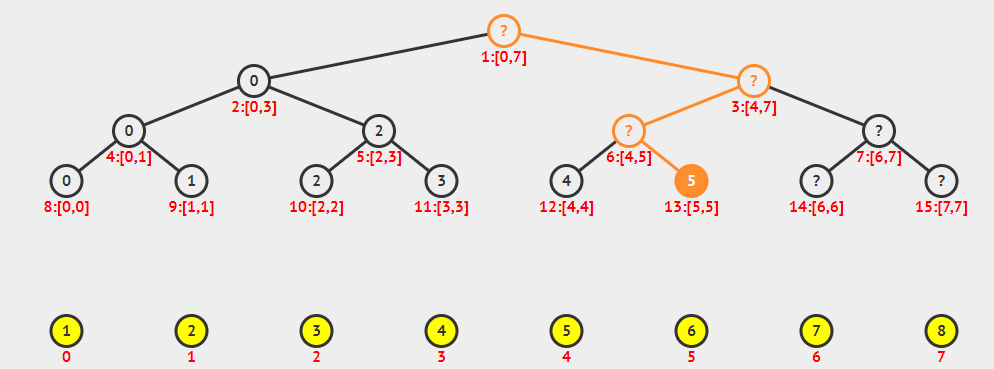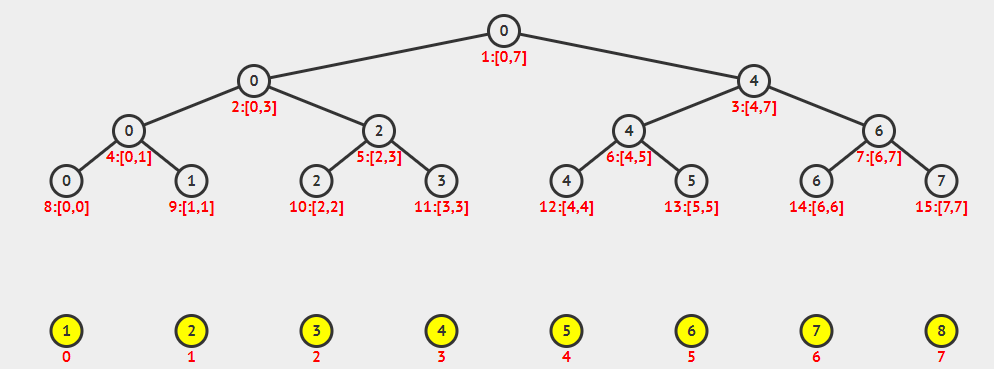
由上图可以看出，线段树除了最后一层之外一定是一棵满二叉树，可以借鉴堆的存储方式，用一个一维数组来存储，对于x号节点：

• 父节点：$\frac{x}{2} \iff x>>1$
• 左儿子节点：$2 \times x \iff x<<1$
• 右儿子节点：$2 \times x+1 \iff x<<1 \mid 1$

问题：对于一个长度为n的区间，树中会有多少节点呢？

最后一层会有n个点，但是最后一层可能满足满二叉树的性质，所以不妨认为倒数第二层有n个点，上面的层的点数一定有n-1个点，最后一层最多有2n个点，所以总共有n-1 + n + 2n = 4n-1个点，所以我们所开的区间长度一般为4n。

时间复杂度

一个包含n个区间的线段树，空间复杂度$O(n)$，查询的时间复杂度则为$O(log(n+k))$，其中k是符合条件的区间数量。

基本操作

注意：pushup操作在build和modify函数中会用到，每更改或加入一个新的数后，需要执行一次pushup操作。

pushdonw操作在modify和query函数中会用到，一旦设计到区间分裂即tr[u].l + tr[u].r >> 1;这句话前面一定要进行pushdown操作

建树

void build(int u, int l, int r)
{
    if (l == r) // 叶子结点
        // 根据题目要求存储需要维护的变量
    else
    {
        tr[u] = {l, r}; // 这一步一定不要往，对于区间，现在要存储的信息尚不明确，但是左右端点是确定的
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

单点更新

假如说现在我们要使一个节点更新,会产生“牵一发而动全身”的效应，所以我们需要对它上面的节点再次更新。

void modify(int u, int x, LL v) // 修改叶子结点
{
    if (tr[u].l == x && tr[u].r == x) // 叶子结点，此时区间长度为1
        // 根据更改操作修改叶子结点的值，然后注意同时更新 tr[u] 维护的所有变量信息
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

区间查询

比如询问区间[L, R]的和或最值，类比修改过程，分类讨论即可：

• 当查找区间在当前区间的左子区间时，递归到左子区间；
• 当查找区间在当前区间的右子区间时，递归到右子区间；
• 否则，这个区间一定是跨越两个子区间的，我们就把它切成2块，分在两个子区间查询。

最后把答案合起来处理就可以了（如查询区间和时就把两块区间的和加起来，查询最大值时就返回两块区间的最大值）。

在做题过程中，遇到了两种不同的模板，下面对其各自应用场景进行说明（线段树初学，正确与否有待商榷）

线段树只维护一个变量，比如最值，最大公约数，区间和等，可以用下面的查询模板，其实就是根据当前节点的区间由它孩子节点转移过来的情况分类，对于最值问题，无非两种情况，即使当前查询区间跨越了树中区间的mid，也只需要比较一次即可得出结果。但是对于求前缀和的问题，当前节点的tmax有三种情况，[单独在左子树，单独在右子树中，跨越左子树和右子树]，所以需要用到第二个查询模板。

int query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) // 树中结点已经被完全包含在[l, r]中了
        return tr[u].v;  

    int mid = tr[u].l + tr[u].r >> 1;
    int res = 0;
    if (l <= mid ) res = query(u << 1, l, r); // 划分区间时将[L, R]划分为[L, mid] 和 [mid + 1, R]
    if (r > mid) res = max(res, query(u << 1 | 1, l, r));
    return res;
}

线段树需要维护多个变量，往往需要返回Node，因为我们维护的数据有很多，上层父节点需要接收的下层传来的数据也有很多

Node query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);  // 整个区间在树中节点的左儿子结点 直接访问左边的查询结果即可
        else if (l > mid) return query(u << 1 | 1, l, r);
        else
        {
            // 否则，区间[l, r]跨越了 结点u的左右孩子节点
            auto left = query(u << 1, l, r);
            auto right = query(u << 1 | 1, l, r);
            Node res;
            pushup(res, left, right); // 根据 left 和 right 这两个儿子节点更新res
            return res;
        }
    }
}

比如 你能回答这些问题吗 这道题，求最大连续字段和，我们需要维护区间和，最大前缀，最大后缀，最大连续字段和这四个变量。

再比如 区间最大公约数 这道题，我们需要维护区间最大公约数和前缀和这两个变量，当然，前缀和也可以用树状数组来维护。

区间修改

区间修改大体可以分为两步：

• 找到区间中全部都是要修改的点的线段树中的区间
• 修改这一段区间的所有点

我们先从根节点出发（根节点一定包含所有的点，包括被修改区间），一直往下走，直到当前区间中的元素全部都是被修改元素。

• 当左区间包含整个被修改区间时，我们就递归到左区间；
• 当右区间包含整个被修改区间时，我们就递归到右区间；

否则，情况一定就如下图所示(要查询的区间[L, R]和树中区间[t[L], t[R]]必然存在交集)：

不过，通过思考，我们可以发现，被修改区间中的元素间，两两之间都不会产生影响。
所以，我们可以把被修改区间分解成两段，使得其中的一段完全在左区间，另一端完全在右区间。
很明显，直接在mid的位置将该区间切开是最好的。

但是直接修改需要把所有包含在[L, R]区间内的点都遍历一遍，时间无法承受，此时就用到了懒标记，也叫延迟标记。

每次查询前需要先进行pushdown操作

void pushdown(int u)
{
    auto &root = tr[u]. &left = tr[u << 1], &right = tr[u << 1 | 1];
    if (root.add) // 如果有懒标记的话
    {
        left.add += root.add, left.sum += (LL)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (LL)(right.r - right.l + 1) * root.add;
        root.add = 0;// 更新完后将根节点的懒标记清空
    }
}

延迟标记

注意：题目中如果只有单点修改，不需要用懒标记就可以保证时间复杂度为 $O(logn)$，涉及到修改一个区间，需要加上懒标记，否则时间复杂度会退化

区间更新的效率很慢，很多同学会想到用一个for循环，每个点走一遍。虽说思维难度不大，而且在点与点范围跳跃速度也不慢，但当要修改的数据到达一定规模时，这样重复的操作会消耗巨量时间，非常容易TLE。所以我们需要找到之间重复的规律，简化程序，以减少不必要的时间浪费。

所以我们想到了加一个延迟标记，简单来说，就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。每次执行修改时，我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。

假设有个大小为 5 的数组$a=\{10,11,12,13,14\}$，要将其转化为线段树，有以下做法：设线段树的根节点编号为 1，用数组 d 来保存我们的线段树，$d_i$ 用来保存线段树上编号为 i 的节点的值（这里每个节点所维护的值就是这个节点所表示的区间总和）。如下图所示：

我们将执行若干次给区间内的数加上一个值的操作。我们现在给每个节点增加一个 $t_i$，表示该节点带的标记值。

最开始时的情况是这样的（为了节省空间，这里不再展示每个节点管辖的区间）：

现在我们准备给 $[3,5]$ 上的每个数都加上 5。根据前面区间查询的经验，我们很快找到了两个极大区间 $[3,3]$ 和 $[4,5]$（分别对应线段树上的 3 号点和 5 号点）。
我们直接在这两个节点上进行修改，并给它们打上标记：

我们发现，3 号节点的信息虽然被修改了（因为该区间管辖两个数，所以 $d_3$ 加上的数是 $5 \times 2=10）$，但它的两个子节点却还没更新，仍然保留着修改之前的信息。不过不用担心，虽然修改目前还没进行，但当我们要查询这两个子节点的信息时，我们会利用标记修改这两个子节点的信息，使查询的结果依旧准确。

接下来我们查询一下$[4,4]$区间上各数字的和。
我们通过递归找到 $[4,5]$ 区间，发现该区间并非我们的目标区间，且该区间上还存在标记。这时候就到标记下放的时间了。我们将该区间的两个子区间的信息更新，并清除该区间上的标记。