新博客粉墨登场,希望各位大佬点赞,评价,收藏

树上差分

算法详解

算法范围

树上差分算法,是一个适用于树上区间操作的算法.

它是差分数组,前缀和求解的树上拓展.

众所周知,树这类特殊的结构,往往具有很多性质,而树上差分往往就是结合这些性质,进行高效率的处理.

我们还需要知道一点,树上差分基本上不会出裸题,往往会和大量的算法结伴出行.

其中,树上差分通常,99%的可能性与LCA最近公共祖先算法,一起出现在题目.就像热恋情人一样

树上差分,准确来说不是算法,而是一种优秀的思想

算法概念

树上差分,捕捉关键字.

1. 树上(体现了适用结构)
2. 差分(体现了思想本质)

说了跟没有讲一样,差评

正经脸嬉皮笑脸的我,跟大家好好胡说八道说一下树上差分,这个有趣变态的算法.

趣闻来也

Acwing是一个大集体,通过网络空间,联络了千万家庭.

现在有大量的网友们,他们手上有大量的学习资源,想要共享给其他人,赚取一个具有神秘力量的东西.(强势为接下来的Acwing积分打广告)

那就是Acwing积分,它无所不能,可以兑换字体,称号,荣誉,权限,甚至AcwingT恤,虽然现在木有等等,等等更加人性化的东西

我们知道,两个人他们相互认识,可能隔着很多人.

因此我们不妨认为,Acwing的网友们,他们组成了一棵树.

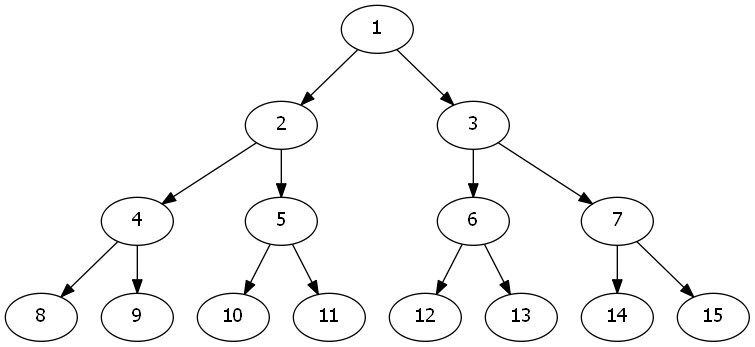
小A同学,想要把自己的资源传输给小B同学,他们需要经过很多人.

本着资源共享的目的,因此路径上的每一个人,都可以得到一份资源.

小A同学,希望自己手上的资源,越早地提供给小B同学,那么他们显然要走一条最短路.

也就是我们的Lca路径.

小A同学是一个资源大户,他总是时不时给小B同学,传输资源.

第一天,小A传给小B,15个yxc老师精品资源,包括算法基础课,算法竞赛进阶指南,Leetcode打卡.

第二天,小A传给小B,7个秦淮岸同学的算法大礼包精品资源.

第三天,小A传给小B,1个Chicago大佬的搜索精品资源.

第四天,小A传给小B,1个Corner小仙女的精品并查集资源.

第五天,小A传给小B,1个林同学的精品贪心资源.

小A同学,小B同学手上的资源数量就是以上总和.

综上所述,我们发现[a,b]节点,路径上的所有节点,他们的值都会增加同样一个值.

显然每天,肯定不止小A和小B同学传资源,肯定有很多人,很多次传输资源.

假如说,我们的Acwing服务器,使用最普通的算法,那么面对茫茫人海,统计每一个节点的资源数量,增加一个区间的资源数量,肯定会崩溃的.

所以,我们的首席技术官,yxc老师想到了树上差分算法.

算法流程

我们发现,差分和前缀和在一起,是可以统计出每一个节点的数量的.

但是此时我们面临的是一棵树,我们该怎么办呢?

先来定义概念
$$ f[i]表示i到i的父亲的边权 \\\\ w[i]表示i的子树权值之和 $$

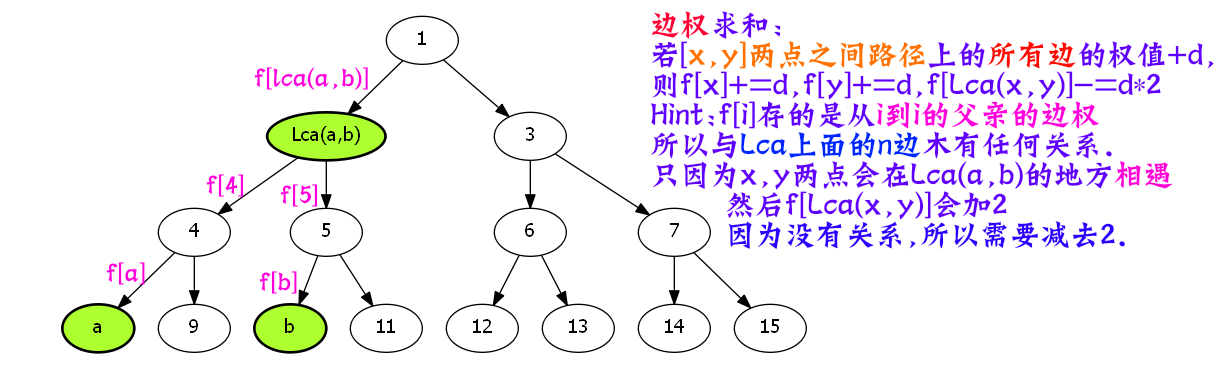
观察这张图,然后思考一下,我们发现了什么.

树上差分,竟然就是DFS序列构成区间的一种差分体现.

我们知道DFS序列,其实就是子树区间.如果不懂,欢迎看秦淮岸的搜索专题讲解,里面有DFS序的讲解

那么树上差分,其实就这么巧妙地转化为了区间差分一样的套路.

在这里,我们只讨论边上差分,暂时不讨论点上差分.

Update:点权差分

其实就是

d[a]++
d[b]++
d[lca(a,b)]--;
d[fa[lca(a,b)]--;

好题选讲

原题连接

题目描述

传说中的暗之连锁被人们称为 Dark。

Dark 是人类内心的黑暗的产物，古今中外的勇者们都试图打倒它。

经过研究，你发现 Dark 呈现无向图的结构，图中有 N 个节点和两类边，一类边被称为主要边，而另一类被称为附加边。

Dark 有 N – 1 条主要边，并且 Dark 的任意两个节点之间都存在一条只由主要边构成的路径。

另外，Dark 还有 M 条附加边。

你的任务是把 Dark 斩为不连通的两部分。

一开始 Dark 的附加边都处于无敌状态，你只能选择一条主要边切断。

一旦你切断了一条主要边，Dark 就会进入防御模式，主要边会变为无敌的而附加边可以被切断。

但是你的能力只能再切断 Dark 的一条附加边。

现在你想要知道，一共有多少种方案可以击败 Dark。

注意，就算你第一步切断主要边之后就已经把 Dark 斩为两截，你也需要切断一条附加边才算击败了 Dark。

输入格式

第一行包含两个整数 N 和 M。

之后 N – 1 行，每行包括两个整数 A 和 B，表示 A 和 B 之间有一条主要边。

之后 M 行以同样的格式给出附加边。

输出格式

输出一个整数表示答案。

数据范围

$$ N \le 100000\\\\ M \le 200000,数据保证答案不超过2^{31}-1 $$

输入样例：

4 1 
1 2 
2 3 
1 4 
3 4 

输出样例：

3

解题报告

题意理解

这道题目题意比较绕,我们来一步步剖解这道题目.题目解剖学,人体解剖学

1. 一颗$n-1$条主要边的树,然后增加了$m$条附加边.

2. 我们只能删除一条主要边,一条附加边,一种边叫做主要边,一种边叫做附加边.

3. 要求删除两条边后,这棵树不再是连通的.

4. 我们需要统计,有多少种方案可以使得不连通,输出方案数.

算法解析

附加边到底有什么用处?
$$ 对于每一条连接x,y节点的(x,y),其实我们都可以认为这条边,连接了(x,y)这条路径上的所有点. $$
当没有了主要边的时候,其实附加边就是我们的主要边.
$$ 所以说,附加边(x,y),就是将树上x,y之间的路径上的每条主要边,都覆盖了一次. $$
因为当$(x,y)$路径上的任意一条主要边消失后,他都可以成为主要边,去维护连通性.

因此现在我们的问题模型转化了.

给定一个$n-1$条边的树,求每一条树边,被非树边覆盖了多少次

1. 树边也就是主要边
2. 非树边也就是附加边

那么这就是一个树上差分统计覆盖次数问题了.
$$ 每一条附加边,使得(x,y)节点的路径上,路径上的每一条主要边的权值+1. $$

此时我们的问题,变成了如何统计方案数.

我们来好好地分类讨论一下主要边,身上的附加边.
$$ 1.主要边被覆盖了0次,即上面只有0条附加边. $$
我们发现删除完这条主要边后,随意删除一条附加边,我们都可以让树不连通.也就是$m$种方案.

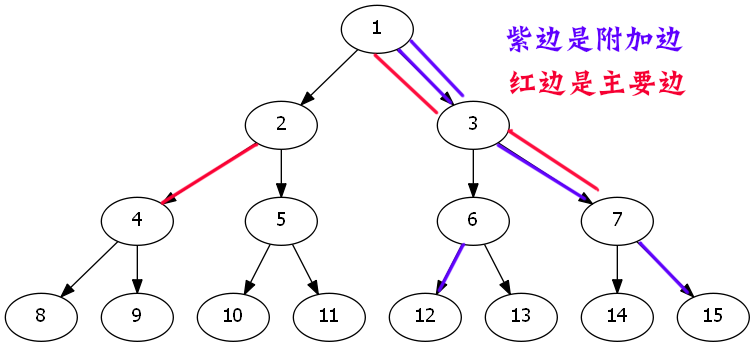
只要删除$(2,4)$这条红边,那么随意一条附加边,都可以满足条件.
$$ 2.主要边覆盖1次,即上面只有一条附加边 $$
我们发现删除完这条主要边后,我们只能删除这条主要边的附加边.也就是$1$种方案.

也就是删除咱们图上面的$(3,7)$红边,然后我们只能删除那条上面的紫色边.
$$ 3.主要边覆盖大于1次,即上面有多条附加边 $$
我们发现,怎么删除,总能连通.于是$0$种方案.

代码解析

#include <bits/stdc++.h>
using namespace std;
const int N=100000+200;
int n,m,ans;
struct LCA
{
    int head[N<<1],Next[N<<1],edge[N<<1],ver[N<<1],tot;
    int deep[N],fa[N][22],lg[N],date[N];
    inline void init()
    {
        memset(head,0,sizeof(head));
        memset(deep,0,sizeof(deep));
        tot=0;
    }
    inline void add_edge(int a,int b,int c)
    {
        edge[++tot]=b;
        ver[tot]=a;
        Next[tot]=head[a];
        head[a]=tot;
    }
    inline void dfs(int x,int y)
    {
        deep[x]=deep[y]+1;//深度是父亲节点+1
        fa[x][0]=y;//2^0=1,也就是父亲节点
        for(int i=1; (1<<i)<=deep[x]; i++) //2^i<=deep[x]也就是别跳出根节点了
            fa[x][i]=fa[fa[x][i-1]][i-1];
        for(int i=head[x]; i; i=Next[i]) //遍历所有的出边
            if (edge[i]!=y)//避免回到父亲节点
                dfs(edge[i],x);//自己的儿子节点, 自己是父亲节点
        return ;
    }
    inline int Lca(int x,int y)//Lca过程
    {
        if (deep[x]<deep[y])//x节点默认深度深一些,在下面
            swap(x,y);//交换
        while(deep[x]>deep[y])//还没有同一高度
            x=fa[x][lg[deep[x]-deep[y]]-1];//往上面跳跃,deep[x]-deep[y]是高度差.-1是为了防止deep[x]<deep[y]
        if(x==y)//意外发现,y就是(x,y)的Lca
            return x;
        for(int i=lg[deep[x]]; i>=0; i--)
            if (fa[x][i]!=fa[y][i])//没有跳到Lca
            {
                x=fa[x][i];//旋转跳跃
                y=fa[y][i];//我闭着眼
            }
        return fa[x][0];//父亲节点就是Lca,因为本身是离着Lca节点最近的节点,也就是Lca的儿子节点.
    }
    inline int query(int x,int f)//f是x节点的父亲节点
    {
        for(int i=head[x]; i; i=Next[i]) //所有出边
        {
            int j=edge[i];//出边
            if (j!=f)//不是父亲节点
            {
                query(j,x);//访问儿子节点
                date[x]+=date[j];//累加子树节点的值
                if(date[j]==0)
                    ans+=m;
                else if(date[j]==1)
                    ans++;
            }
        }
    }
    inline int update(int x,int y)//修改操作,x,y节点构成的路径统一+1
    {
        date[x]++;
        date[y]++;
        date[Lca(x,y)]-=2;
    }
} g1;
int main()
{
    scanf("%d%d",&n,&m);
    g1.init();
    for(int i=1; i<n; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        g1.add_edge(a,b,0);//加边
        g1.add_edge(b,a,0);//无向图
    }
    for(int i=1; i<=n; i++)
        g1.lg[i]=g1.lg[i-1]+(1<<g1.lg[i-1]==i);//处理log数组的关系
    g1.dfs(1,0);
    for(int i=1; i<=m; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        g1.update(a,b);//附加边
    }
    g1.query(1,0);
    printf("%d\n",ans);
    return 0;
}