欢迎在我的 Luogu 博客上观看！Luogu Blog

欢迎大家点赞收藏。

开头先扔板子：多项式板子们

定义

多项式（polynomial）是形如 $P(x) = \sum \limits_{i = 0}^{n} a_i x ^ i$ 的代数表达式。其中 $x$ 是一个不定元。

$\partial(P(x))$ 称为这个多项式的次数。

多项式的基本运算

• 多项式的加减法

$$A(x) = \sum_{i = 0}^{n} a_i x ^ i, B(x) = \sum_{i = 0}^{m} b_i x ^ i$$

$$A(x) \pm B(x) = \sum_{i = 0}^{\max(n, m)} (a_i \pm b_i) x ^ i$$

• 多项式的乘法

$$A(x) \times B(x) = \sum_{k = 0}^{nm} \sum_{i + j = k} a_i b_j x ^ k$$

• 多项式除法

这里讨论多项式的带余除法。

可以证明，一定存在唯一的 $q(x), r(x)$ 满足 $A(x) = q(x) B(x) + r(x)$，且 $\partial(r(x)) < \partial(B(x))$。

$q(x)$ 称为 $B(x)$ 除 $A(x)$ 的商式，$r(x)$ 称为 $B(x)$ 除 $A(x)$ 的余式。记作：

$$A(x) \equiv r(x) (\bmod \ B(x))$$

特别的，若 $r(x) = 0$，则称 $B(x)$ 整除 $A(x)$，$A(x)$ 是 $B(x)$ 的一个倍式，$B(x)$ 是 $A(x)$ 的一个因式。记作 $B(x) | A(x)$。

有关多项式的引理

• 对于 $n + 1$ 个点可以唯一确定一个 $n$ 次多项式。

• 如果 $f(x), g(x)$ 都是不超过 $n$ 次的多项式，且它对于 $n +1$ 个不同的数 $\alpha_1, \alpha_2 \cdots \alpha_n$ 有相同的值，即 $\forall i \in [1, n + 1], i \in \mathbb{Z}, f(\alpha_i) = g(\alpha_i)$。则 $f(x) = g(x)$。

多项式的点值表示

如果选取 $n + 1$ 个不同的数 $x_0, x_1, \cdots x_n$ 对多项式进行求值，得到 $A(x_0), A(x_1) \cdots A(x_n)$，那么就称 $\{(x_i, A(x_i)) \ | \ 0 \le i \le n, i \in \mathbb{Z} \}$ 为 $A(x)$ 的点值表示。

快速傅里叶变换（FFT）

快速傅里叶变换是借助单位根进行求值和插值，从而快速进行多项式乘法的算法。

单位根

将复平面上的单位圆均分成 $n$ 份，从 $x$ 轴数，第 $i$ 条线与单位圆的交点称为 $i$ 次单位根，记作 $\omega_{n}^{i}$。

根据定义，可以得到：$\omega_{n}^{1} = i \sin \alpha +\cos \alpha, \alpha = \frac{2 \pi}{n}$。

引理：欧拉公式

$\forall \theta \in R$，$e ^ {i\theta} = i\sin \theta + \cos \theta$。

根据欧拉公式，可以得到：$\omega_{n}^{1} = e ^ {\frac{2 \pi i}{n}}$。

由此那么可以得到下面的性质：

• $\omega_{n}^{i} \times \omega_{n}^{j} = \omega_{n}^{i + j}$

• $\omega_{n}^{i + \frac{n}{2}} = - \omega_{n}^{i}$

• $\omega_{n}^{i + n} = \omega_{n}^{i}$

另外一种理解方式是通过棣莫弗公式。

引理：棣莫弗公式

$\forall \theta \in R$，$(\cos \theta + i \sin \theta) ^ n = \cos (n\theta) + i \sin (n\theta)$

考虑两个复平面上的向量

$$z_1 = \rho_1(cos \theta_1 + i \sin \theta_1), z_2 = \rho_2(cos \theta_2 + i \sin \theta_2)$$

计算两个向量相乘的结果，可得：

$$z_1 z_2 = \rho_1 \rho_2 (\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2))$$

当 $\theta_1 = \theta_2, \rho_1 = \rho_2$ 时便是大名鼎鼎的棣莫弗公式。

因此可以得到，单位圆上的两个复数相乘，模长不变（也就是还在单位圆上），幅角相加。然后可以由此理解上面的三个单位根性质。

离散傅里叶变换（DFT）

离散傅里叶变换，是将 $\omega_{n}^{k}, 0 \le k < n$ 代入 $f(x)$ 和 $g(x)$ 中求值的过程。

对于朴素的方法，每次代入一个单位根，然后用 $O(n)$ 的复杂度计算函数值。时间复杂度 $O(n ^ 2)$。

离散傅里叶变换利用了单位根的性质巧妙优化了这个过程。离散傅里叶变换过程如下：

首先将 $f(x)$ 根据次数的奇偶性拆成两部分，分别分为：

$$\begin{cases} e(x) = \sum \limits_{i = 0}^{\frac{n - 2}{2}} a_{2i} x ^ {2i} = a_0 + a_2 x^2 + a_4 x^4 \cdots a_{n - 2} x^{n - 2} \\\\ o(x) = \sum \limits_{i = 0}^{\frac{n - 2}{2}} a_{2i + 1} x ^ {2i + 1} = a_1 x + a_3 x^3 + a_5 x^5 \cdots a_{n - 1} x^{n - 1} \end{cases}$$

设

$$\begin{cases} e’(x) = \sum \limits_{i = 0}^{\frac{n - 2}{2}} a_{2i} x ^ i = a_0 + a_2 x + a_4 x^2 \cdots a_{n - 2} x^{\frac{n - 2}{2}} \\\\ o’(x) = \sum \limits_{i = 0}^{\frac{n - 2}{2}} a_{2i + 1} x ^ {i} = a_1 + a_3 x^1 + a_5 x^2 \cdots a_{n - 1} x^{\frac{n - 2}{2}} \end{cases}$$

则 $f(x) = e’(x ^ 2) + x o’(x ^ 2)$。

将 $\omega_{n}^{k}$ 代入得到：

$$\begin{cases} f(\omega_{n}^{k}) = e’((\omega_{n}^{k}) ^ 2) + \omega_{n}^{k} o’((\omega_{n}^{k}) ^ 2) = e’(\omega_{n}^{2k}) + \omega_{n}^{k} o’(\omega_{n}^{2k}) \\\\ \\ f(\omega_{n}^{k + \frac{n}{2}}) = e’((\omega_{n}^{k+ \frac{n}{2}}) ^ 2) + \omega_{n}^{k+ \frac{n}{2}} o’((\omega_{n}^{k+ \frac{n}{2}}) ^ 2) = e’(\omega_{n}^{2k}) - \omega_{n}^{k} o’(\omega_{n}^{2k}) \end{cases}$$

然后你发现，$f(\omega_{n}^{k})$ 和 $f(\omega_{n}^{k + \frac{n}{2}})$ 仅仅差了一个符号！！！

所以只需要求出 $e’(x)$ 和 $o’(x)$ 对 $\omega^{k}_{n}$（$0 \le k \le \frac{n}{2}$）上的取值，就可以推出 $f(x)$ 在两倍点数上的取值。

每次问题规模缩小一半，因此时间复杂度 $O(n \log n)$。

离散傅里叶逆变换（IDFT）

假设对于两个多项式都得到了 $t = n + m - 1$ 个点值，设为 $\{(x_i, A(x_i)) \ | \ 0 \le i < t, i \in \mathbb{Z} \}, \{(x_i, B(x_i)) \ | \ 0 \le i < t, i \in \mathbb{Z} \}$。

那么可以知道，多项式 $C(x) = A(x) \times B(x)$ 的点值表示一定为：

$$\{(x_i, A(x_i) B(x_i)) \ | \ 0 \le i < t, i \in \mathbb{Z} \}$$
现在，只需要将这 $t$ 个点插值回去，就可以得到 $A(x)B(x)$ 了。

先设这 $t$ 个点值分别是：$\{(x_i, v_i) \ | \ 0 \le i < t, i \in \mathbb{Z} \}$，设最后的多项式为 $C(x) = \sum \limits_{i = 0}^{n + m - 2} c_i x^i$，这里直接给出结论：

$$c_k = \dfrac{1}{n} \sum_{i = 0}^{t - 1} v_i \omega_{t}^{-ki}$$

由此可见，IDFT 和 DFT 仅仅有一个负号的区别。只要将所有的单位根从 $\omega_{n}^{k}$ 变成 $\omega_{n}^{-k}$ 即可。

void FFT(cp a[], int n, int op) {
    if (n == 1) return;
    cp a1[n], a2[n];
    rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
    FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
    cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
    cp Wk = {1, 0};
    rop(i, 0, n >> 1) {
        a[i] = a1[i] + Wk * a2[i];
        a[i + (n >> 1)] = a1[i] - Wk * a2[i];
        Wk = Wk * Wn;
    }
}
void FFT(cp a[], cp b[], int n, int m) {
    m = n + m; n = 1;
    while (n <= m) n <<= 1;
    FFT(a, n, 1); FFT(b, n, 1);
    rop(i, 0, n) a[i] = a[i] * b[i];
    FFT(a, n, -1);
    rep(i, 0, m) a[i].x = a[i].x / n;
}

FFT 优化

• 三次变两次优化

原本的朴素 FFT，将 $\{a\}, \{b\}$ 两个序列分别求值，乘起来再 IDFT 插值一下，一共跑了三次 FFT。这是不好的。

三次变两次优化是这样的：将原序列合并成一个复数：$\{a_i + b_i \times i\}$。做一遍 DFT 把求出的每个函数值平方。因为 $(a + bi) ^ 2 = (a ^ 2 - b ^ 2) + (2abi)$。因此把虚部取出来以后除以 $2$ 就是答案。

void FFT(cp a[], int n, int op) {
    if (n == 1) return;
    cp a1[n], a2[n];
    rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
    FFT(a1, n >> 1, op), FFT(a2, n >> 1, op);
    cp Wn = {cos(2 * pi / n), op * sin(2 * pi / n)};
    cp Wk = {1, 0};
    rop(i, 0, n >> 1) {
        a[i] = a1[i] + a2[i] * Wk;
        a[i + (n >> 1)] = a1[i] - a2[i] * Wk;
        Wk = Wk * Wn;
    }
}
int main() {
    read(n, m);
    rep(i, 0, n) scanf("%lf", &a[i].x);
    rep(i, 0, m) scanf("%lf", &a[i].y);
    m = n + m; n = 1;
    while (n <= m) n <<= 1;
    FFT(a, n, 1);
    rop(i, 0, n) a[i] = a[i] * a[i];
    FFT(a, n, -1);
    rep(i, 0, m) printf("%d ", (int)(a[i].y / 2 / n + 0.5));
}

• 蝴蝶变换优化

后面再补吧。其实本人感觉这个优化不是那么必要，因为三次变两次实在太快了。

FFT 例题

1. A * B problem(plus)

可以设 $x = 10$，把 $a$ 写成 $A(x) = \sum \limits_{i = 0}^{n} a_i x^i$ 的形式（$n = \log_{10} a$）。同理可以把 $b$ 转化为多项式 $B(x)$。

这样求两个数相乘就是求 $A(x) \times B(x)$ 啊。

所以直接 $O(n \log n)$ 做完了。

1. P3338 [ZJOI2014] 力

给出 $n$ 个数 $q_1,q_2, \dots q_n$，定义

$$F_j~=~\sum_{i = 1}^{j - 1} \frac{q_i \times q_j}{(i - j)^2}~-~\sum_{i = j + 1}^{n} \frac{q_i \times q_j}{(i - j)^2}$$

$$E_i~=~\frac{F_i}{q_i}$$

对 $1 \leq i \leq n$，求 $E_i$ 的值。

首先发现这个除以 $q_i$ 就是没用。所以可以化简成：

$$E_j = \sum_{i = 1}^{j - 1} \frac{q_i}{(i - j)^2}~-~\sum_{i = j + 1}^{n} \frac{q_i}{(i - j)^2}$$

先看前面这个式子。答案就是：

$$(j - 1) ^ 2 q_1 + (j - 2) ^ 2 q_2 + (j - 3) ^ 2 q_3 \cdots$$

设 $f(x) = \sum q_i x ^ i, g(x) = \dfrac{1}{i ^ 2} x ^ i$。可以发现，$E_j’ = (f \times g)[j]$

再看后面这一块的式子。我们把 $f(x)$ 的系数翻转，变成 $f’(x) = \sum q_{n - j + 1} x ^ j$。那么可以发现 $E_{j}’‘ = (f’ \times g)[n - j + 1]$。

跑两次 FFT 就完事了。

1. P3723 [AH2017/HNOI2017] 礼物

首先发现加减相对于两个手环是对称的。因此可以把对一个手环的减法转化成对另一个手环的加法。这样可以假设全是在第一个手环上执行的加减操作。

第一个手环执行了加 $c$ 的操作，且旋转过之后的序列为 $[x_1, x_2 \cdots x_n]$，第二个手环为 $[y_1, y_2 \cdots y_n]$。计算差异值并化简，可以得到差异值是：

$$\sum x ^ 2 + \sum y ^ 2 + c ^ 2 n + 2c(\sum x - \sum y) - 2 \sum xy$$

可以发现，这个序列只有最后一项是不定的。

因此将 $y$ 序列翻转后再复制一倍，与 $x$ 卷积，答案就是卷积后序列的 $n + 1 \sim 2n$ 项系数的 $\max$。

直接暴力枚举 $c$，加上前面依托就行了。

$\text{AC code}$

快速数论变换（NTT）

快速数论变换就是基于原根的快速傅里叶变换。

首先考虑快速傅里叶变换用到了单位根的什么性质。

1. $\omega_{n}^{k}, 0 \le k < n$ 互不相同。

2. $\omega_{n}^{k} = \omega_{n}^{k + \frac{n}{2}}$。

3. $\omega_{n}^{k} = \omega_{2n}^{2k}$。

数论中，原根恰好满足这些性质。

对于一个素数的原根 $g$，设 $g_n = g ^ {\frac{p - 1}{n}}$。那么：

$$g_n ^ n = g ^ {p - 1} \equiv 1(\bmod \ p)$$

$$g_n ^ {\frac{n}{2}} = g ^ {\frac{p - 1}{2}} \equiv - 1(\bmod ~ p)$$

$$g ^ \alpha + g ^ \beta = g ^ {\alpha + \beta}$$

$$g_{\alpha n}^{\alpha k} = g_{n}^{k}$$

我们发现它满足 $\omega_{n}^{k}$ 的全部性质！

因此，只需要用 $g_{n}^k = g_{}^{\frac{p - 1}{n} k}$ 带替全部的 $\omega_{n}^{k}$ 就可以了。

tips：对于一个质数，只有当它可以表示成 $p = 2 ^ \alpha + 1$，且需要满足多项式的项数 $< \alpha$ 时才能使用 NTT。$p$ 后面有个加一，是因为 $g_n$ 指数的分子上出现了 $-1$；$p - 1$ 需要时二的整数次幂，是因为每次都要除以 $2$。

bonus：常用质数及原根

$p = 998244353 = 119 \times 2 ^ {23} + 1, g = 3$

$p = 1004535809 = 479 \times 2 ^ {21} + 1, g = 3$

void NTT(int *a, int n, int op) {
    if (n == 1) return;
    int a1[n], a2[n];
    rop(i, 0, n >> 1) a1[i] = a[i << 1], a2[i] = a[(i << 1) + 1];
    NTT(a1, n >> 1, op), NTT(a2, n >> 1, op);
    int gn = qpow((op == 1 ? g : invg), (mod - 1) / n), gk = 1;
    rop(i, 0, n >> 1) {
        a[i] = (a1[i] + 1ll * gk * a2[i]) % mod;
        a[i + (n >> 1)] = (a1[i] - 1ll * gk * a2[i] % mod + mod) % mod;
        gk = 1ll * gk * gn % mod;
    }
}

NTT 优化：蝴蝶变换

盗大佬一张图

这是进行 NTT 的过程中数组下标的变化。

这样看似乎毫无规律。但是把他们写成二进制：

变换前：$000 ~ 001 ~ 010 ~ 011 ~ 100 ~ 101 ~ 110 ~ 111$

变换后：$000 ~ 100 ~ 010 ~ 110 ~ 001 ~ 101 ~ 011 ~ 111$

可以发现，就是对每个下标进行了二进制翻转。

因此可以先预处理出每个下标在递归底层对应的新下标。然后从底层往顶层迭代合并。

预处理每个下标的二进制翻转：

rop(i, 0, n) rev[i] = rev[i >> 1] >> 1 | (i & 1) << bit;

优化后的 NTT：

void NTT(int *a, int n, int op) {
    rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
    for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
        int gn = qpow((op == 1 ? g : invg), (mod - 1) / (mid << 1));
        for (int i = 0, gk = 1; i < n; i += (mid << 1), gk = 1)
            for (int j = 0; j < mid; j ++ , gk = 1ll * gk * gn % mod) {
                int x = a[i + j], y = 1ll * a[i + j + mid] * gk % mod;
                a[i + j] = Mod(x + y), a[i + j + mid] = Mod(x - y);
            }
    }
}

当然了，FFT 也可以用蝴蝶变换来优化。实践证明，速度变快了至少二分之一。

FFT 的迭代实现

void FFT(cp *a, int n, int op) {
    rop(i, 0, n) if (i < rev[i]) swap(a[i], a[rev[i]]);
    for (int mid = 1; (mid << 1) <= n; mid <<= 1) {
        cp Wn = {cos(pi / mid), op * sin(pi / mid)};
        for (int i = 0; i < n; i += (mid << 1)) {
            cp Wk = {1, 0};
            for (int j = 0; j < mid; j ++ , Wk = Wk * Wn) {
                cp x = a[i + j], y = Wk * a[i + j + mid];
                a[i + j] = x + y, a[i + j + mid] = x - y;
            }
        }
    }
}

任意模数多项式乘法（MTT）

计算 $f \times g(\bmod ~ p)$ 的结果（$p$ 不一定能够表示成 $2 ^ \alpha + 1$ 的形式）。

这个东西有两种做法，但是我只学会了三模 NTT。

首先，卷积之后每个系数最多达到 $\max \{V\} ^ 2 \times n$ 的大小。拿模板题举例，这个东西就是 $10 ^ {23}$。因此只需要找三个模数 $p_1, p_2, p_3$，满足 $p_1p_2p_3 > \max \{V\} ^ 2 \times n$，然后用他们分别 NTT，最后再 CRT / exCRT 合并即可。

int CRT(int a, int b, int c, int p) {
    int k = 1ll * Mod(b - a, p2) * inv1 % p2;
    LL x = 1ll * k * p1 + a;
    k = 1ll * Mod((c - x) % p3, p3) * inv2 % p3;
    x = (x + 1ll * k * p1 % p * p2 % p) % p;
    return x;
}
void MTT(int *a, int n, int *b, int m, int p) {
    int B = ((n + m) << 2) + 1;
    rev = new int [B]();
    int *a1 = new int [B](), *b1 = new int [B]();
    int *a2 = new int [B](), *b2 = new int [B]();
    int *a3 = new int [B](), *b3 = new int [B]();
    rop(i, 0, B) 
        a1[i] = a2[i] = a3[i] = a[i], b1[i] = b2[i] = b3[i] = b[i];
    NTT(a1, n, b1, m, p1); NTT(a2, n, b2, m, p2); NTT(a3, n, b3, m, p3);
    inv1 = inv(p1, p2); inv2 = inv(1ll * p1 * p2 % p3, p3);
    rep(i, 0, n + m) a[i] = CRT(a1[i], a2[i], a3[i], p);
}

这里选择的模数为：$p_1 = 998244353, p_2 = 469762049, p_3 = 1004535809$。他们的原根都为 $g = 3$。

多项式求逆

求多项式 $f(x)$ 的逆元 $f^{-1}(x)$。$f(x)$ 的逆元定义为满足 $f(x) g(x) = 1(\bmod \ x ^ n)$ 的多项式 $g(x)$。

使用倍增法即可求出多项式的逆元。

首先假设已经求出了 $f(x) g’(x) \equiv 1(\bmod \ x ^ {\lceil \frac{n}{2} \rceil})$。再假设 $f(x) \bmod \ x ^ n$ 意义下逆元为 $g(x)$。那么有：

$$g(x) \equiv g’(x) (\bmod \ x ^ {\lceil \frac{n}{2} \rceil})$$

$$(g(x) - g’(x)) \equiv 0 (\bmod \ x ^ {\lceil \frac{n}{2} \rceil})$$

$$(g(x) - g’(x)) ^ 2 \equiv 0 (\bmod \ x ^ n)$$

$$g^2(x) - 2 g(x) g’(x) + g’^2(x) \equiv 0 (\bmod \ x ^ {n})$$

两边同时乘以 $f(x)$，可以得到：

$$g(x) - 2 g’(x) + f(x) g’^2(x) \equiv 0 (\bmod \ x ^ n)$$

$$g(x) \equiv 2g’(x) - f(x) g’^2(x) (\bmod \ x ^ n)$$

$$g(x) \equiv g’(x) (2 - f(x)g’(x)) (\bmod \ x ^ n)$$

倍增求即可。

void Inv(int *f, int *g, int n) {
    if (n == 1) {
        g[0] = inv(f[0]); return;
    } Inv(f, g, (n + 1) >> 1);
    int m = 1, bit = 0;
    while (m < (n << 1)) m <<= 1, bit ++ ; bit -- ;
    rop(i, 0, n) tmp[i] = f[i];
    rop(i, n, m) tmp[i] = 0;
    rev = new int [m + 5]();
    rop(i, 1, m) rev[i] = (rev[i >> 1] >> 1) | (i & 1) << bit;
    NTT(tmp, m, 1); NTT(g, m, 1);
    rop(i, 0, m) g[i] = (2ll - 1ll * g[i] * tmp[i] % p + p) % p * g[i] % p;
    NTT(g, m, -1); int invn = inv(m);
    rop(i, 0, m) g[i] = 1ll * g[i] * invn % p;
    rop(i, n, m) g[i] = 0; 
    free(rev); rev = NULL;
}

分治 FFT

给定序列 $g_{1\dots n - 1}$，求序列 $f_{0\dots n - 1}$。

其中 $f_i=\sum_{j=1}^if_{i-j}g_j$，边界为 $f_0=1$。

答案对 $998244353$ 取模。

其实这是个多项式求逆板子

首先考虑生成函数 $F(x) = \sum _{i = 0}^{+ \infty} f_i x ^ i, G(x) = \sum _{i = 0}^{ + \infty}g_i x ^ i$。然后可以发现：

$$F(x) G(x) = \sum \limits_{k = 0}^{+\infty} x ^ k \sum \limits_{i + j = k}^{} f_i g_j = F(x) - f_0 x^0$$

因此 $F(x)(G(x) - 1) = -f_0$，也就是：

$$F(x) \equiv \dfrac{f_0}{1 - G(x)} (\bmod \ x ^ n)$$

所以直接设 $g_0 = 0$，然后把 $1 - g$ 求逆就行了。

read(n);
rop(i, 1, n) read(g[i]);
rop(i, 1, n) g[i] = Poly::p - g[i];
(g[0] += 1) %= Poly::p; Poly::Inv(g, n);
rop(i, 0, n) write(' ', g[i]); return 0;

多项式对数函数（Polyln）

给定 $f(x)$，求多项式 $g(x)$ 使得 $g(x) \equiv \ln(f(x)) (\bmod \ x ^ n)$

前置知识：简单的求导和积分，以及基本的多项式模板。

首先设 $h(x) = \ln(x)$，那么

$$g(x) \equiv h(f(x)) (\bmod \ x ^ n)$$

然后对同余方程两边同时求导，得到

$$g’(x) \equiv [h(f(x))]’ (\bmod \ x ^ n)$$

根据复合函数求导公式 $f’(g(x)) = f’(g(x))g’(x)$ 可得，

$$g’(x) \equiv h’(f(x))f’(x)(\bmod \ x ^ n)$$

然后又有 $\ln ‘(x) = \dfrac{1}{x}$，因此

$$g’(x) \equiv \dfrac{f’(x)}{f(x)}$$

计算 $f’(x)$ 和 $f^{-1}(x)$ 作为 $a, b$。计算 $a \times b (\bmod \ 998244353)$ 得到 $g’(x)$ ，然后求 $g’(x)$ 的积分就好了。

积分公式：$\int x ^ a \mathrm{dx} = \dfrac{1}{a + 1} x ^ {a + 1}$。

void der(int *f, int n) { rep(i, 1, n) f[i - 1] = 1ll * i * f[i] % p; f[n] = 0; }
void Int(int *f, int n) {dep(i, n, 1) f[i] = 1ll * inv(i) * f[i - 1] % p; f[0] = 0; }
void Ln(int *f, int n) {
    int B = (n << 2) + 5; int *_f = new int[B]();
    rep(i, 0, n) _f[i] = f[i];
    der(_f, n), Inv(f, n);
    NTT(f, n, _f, n); Int(f, n);
    free(_f); _f = NULL;
}

多项式指数函数（PolyExp）

给定多项式 $f(x)$，求 $g(x)$ 满足 $g(x) \equiv e ^ {f(x)} (\bmod \ x ^ n)$。

前置知识：牛顿迭代。

牛顿迭代是用来求函数零点的有力工具。

例如，下面这个图是使用牛顿迭代法求 $f(x)=x^4+3 x^2+7 x+3$ 零点的过程。

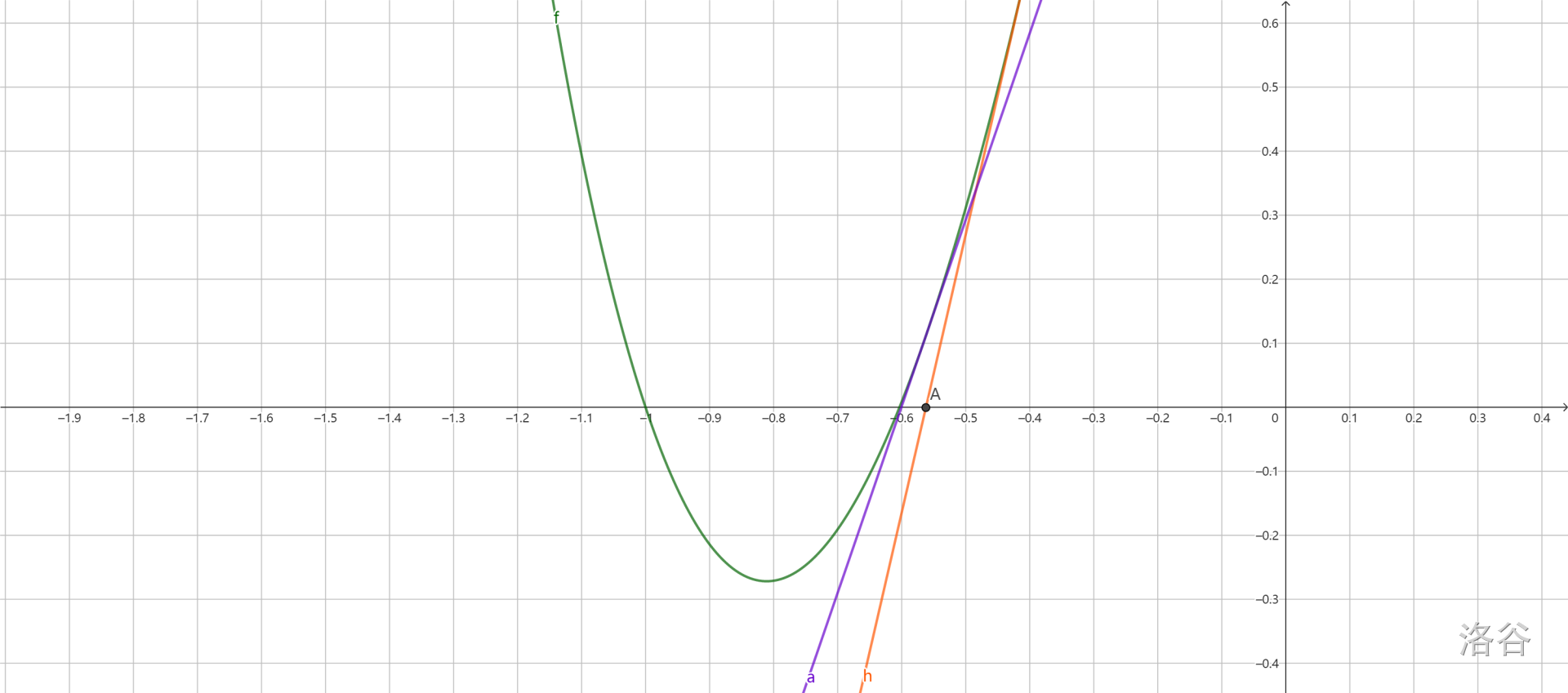
首先，随便选择一个点 $(x_0, f(x_0))$，过这个点做 $f(x)$ 的切线。切线方程是 $y = f’(x_0)(x - x_0) + f(x_0)$。它与 $x$ 轴交于一点 $A(-0.56243, 0)$。

接下来，再令 $x_1 = -0.56243$，过点 $(x_1, f(x_1))$ 再做 $f(x)$ 的切线，与 $x$ 轴交于点 $B(-0.60088, 0)$。

再令 $x_2 = -0.60088$，如此迭代下去。可以发现，$x_n$ 会逐渐逼近零点。

刚才说切线方程为 $y = f’(x_0)(x - x_0) + f(x_0)$。如果令 $y = 0$，得到的 $x$ 便是切线方程与 $x$ 轴的交点，为

$$x = x_0 - \dfrac{f(x_0)}{f’(x_0)}$$

运用于多项式，假设要求使 $f(g(x)) \equiv 0(\bmod \ x ^ n)$ 的多项式 $g(x)$，并且已经知道 $f(g_0(x)) \equiv 0 (\bmod \ x ^ {\frac{n}{2}})$。

那么可以说，

$$g(x) = g_0(x) - \dfrac{f(g_0(x))}{f’(g_0(x))}$$

接下来解决多项式 Exp。所求为 $g(x)$ 使得 $g(x) \equiv e ^ {f(x)} (\bmod \ x ^ n)$。两边都取 $\ln$ 得到：

$$\ln g(x) \equiv f(x) (\bmod \ x ^ n)$$

移项得：

$$\ln g(x) - f(x) \equiv 0 (\bmod \ x ^ n)$$

设 $F(g(x)) = ln g(x) - f(x)$，那么所求就是 $F(x)$ 的零点。

假设已经有 $g_0(x)$ 使得 $F(g_0(x)) \equiv 0 (\bmod \ x ^ {\frac{n}{2}})$，根据上面的牛顿迭代，有：

$$g(x) = g_0(x) - \dfrac{F(g_0(x))}{F’(g_0(x))} = g_0(x) - \dfrac{\ln g_0(x) - f(x)}{\frac{1}{g_0(x)}} = g_0(x)(1 - \ln g_0(x) +f(x))$$

根据这个柿子倍增求即可。每次需要计算一个 $\ln$，一个乘法，时间 $O(n \log n)$。

写的有点丑，超级大肠数。

void Exp(int *f, int *g, int n) {
    if (n == 1) return void(g[0] = 1);
    Exp(f, g, (n + 1) >> 1);
    int B = (n << 2) + 5; int *lnb = new int[B]();
    rop(i, 0, n) lnb[i] = g[i]; Ln(lnb, n);
    tmp = new int[B](); rop(i, 0, n) tmp[i] = f[i];
    rop(i, 0, n) tmp[i] = (1ll * tmp[i] - lnb[i] + p) % p;
    tmp[0] ++ ; NTT(g, n, tmp, n);
    free(tmp); tmp = NULL; free(lnb); lnb = NULL;
}

多项式快速幂（PolyPower）

在模 $x ^ n$ 意义下计算 $f^k(x)$。

有了前面的知识铺垫，这部分就非常的简单。

根据对数恒等式，有 $f(x) = e ^ {\ln f(x)}$。

因此 $f^k(x) = e ^ {k \ln f(x)}$。

把 $f(x)$ 乘以 $k$，求多项式 $\ln$，然后再 $\exp$ 回来就行了。

void Power(int *f, int n, int k) {
    Ln(f, n); rop(i, 0, n) f[i] = 1ll * f[i] * k % p; Exp(f, n);
}

多项式开根

在模 $x ^ n$ 意义下计算 $f^{\frac{1}{k}}(x)$。

这个最简单。直接把 $\frac{1}{k} \bmod p$，然后多项式快速幂。