算法理解

定义

树的直径的定义

在一棵树中，每一条边都有权值，树中的两个点之间的距离，定义为连接两点的路径上边权之和，那么树上最远的两个点，他们之间的距离，就被称之为，树的直径。

树的直径的别称，树的最长链。

请注意：树的直径，还可以认为是一条路径，不一定是只是一个数值。

求法

树型DP

我们假如说，设$1$号节点为根节点，那么一张$N$个点，$N-1$条边的无向图,我们可以认为它是一棵有根树。

我们不妨设$D[x]$表示从节点$x$出发，以$x$为根的子树，能过到达最远节点的距离。

也就是对于$x$节点而言的最长链。

Hint:不过请注意一个点，x到达自己子树节点的最长距离，不是到达非子树节点的最长距离.

一句人话就是：x不可以抵达父亲节点，爷爷节点，兄弟节点，只可以管自己家的人，只可以管儿子节点，孙子节点，曾孙子节点。。。。。

那么假如说。
$$ y_i \in {son[x]} $$
也就是集合$y$，都是$x$节点的儿子节点。

一个显然的公式就出来了。
$$ d[x]=max(d[x],d[y_i]+ver[x][y_i]) $$
这句话是什么意思，也就是说。
$$ x节点的最长链=一个儿子y_i节点的最长链，加上x节点到儿子y_i节点的距离。 $$
但是我们知道。
$$ 树的直径=最长链+次长链 $$
那么我们思考一下,关于$x$节点的最长链推导的过程。
$$ if (d[x]<d[y_i]+ver[x][y_i]) \\\\ \quad \quad d[x]=d[y_i]+ver[x][y_i] $$
假如说推导之前
$$ d[x]=5 $$
然后突然又出现了一条链
$$ d[y_i]+ver[x][y_i]=6 $$
那么此时我们发现，一个非常重要的点，就是。
$$ d[x]为次长链 \\\\ d[y_i]+ver[x][y_i]为最长链 $$

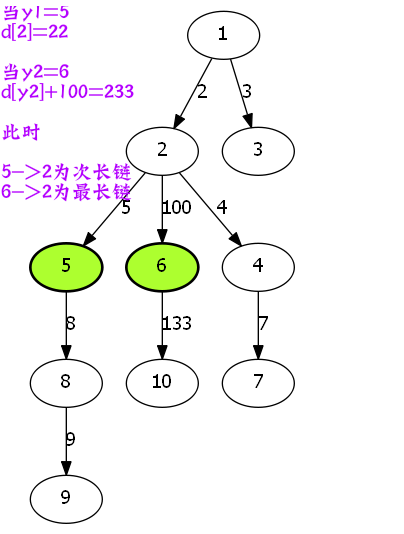
所以说，我们的求解过程，也就不难了。

直接上代码了。

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+20;
int head[N],edge[N],ver[N],Next[N],tot;
int d[N],ans;
bool vis[N];
void dp(int x)
{
    vis[x]=1;//已经访问
    for(int i=head[x]; i; i=Next[i])
    {
        int y=edge[i];//儿子节点
        if (vis[y])//已经访问了，不能再访问了
            continue;
        dp(y);//先处理儿子节点，求出儿子节点的最长链
        ans=max(ans,d[x]+d[y]+ver[i]);//最长链+次长链
        d[x]=max(d[x],d[y]+ver[i]);//更新
        //如果说d[x]>d[y]+ver[i]，那么d[x]为最长链，d[y]+ver[i]有可能为次长链，但是所有儿子遍历完后，次长链一定在这里会出现
        //如果说d[x]<d[y]+ver[i]，那么d[x]为次长链，d[y]+ver[i]为最长链
    }
}
void init()
{
    //自行补充 
}
int main()
{
    init();//读入 
    dp(1);
    return 0;
}

两次搜索求解

如果说题目要我们，找到这条树的直径上，具体的每一个节点，那么这该怎么办呢？

1. 随意选一个点$x$，开始搜索，找到离着当前节点最远的节点$y$。
2. 从上一轮搜索到的最远节点$y$，再次搜索一遍，找到离这个节点最远的节点$z$

因此我们发现，$y$节点到$z$节点的路径，就是树的直径，又因为是搜索，所以我们可以统计路径上经过了哪些节点。

代码就不打了，下面的这道题目，有这两种算法的代码。

原题链接
更好的阅读体验,新博客希望各位大佬关注QwQ

题目描述

在一个地区有 n 个村庄，编号为1,2,…,n。

有 n-1 条道路连接着这些村庄，每条道路刚好连接两个村庄，从任何一个村庄，都可以通过这些道路到达其他任一个村庄。

每条道路的长度均为1个单位。

为保证该地区的安全，巡警车每天都要到所有的道路上巡逻。

警察局设在编号为1的村庄里，每天巡警车总是从警局出发，最终又回到警局。

为了减少总的巡逻距离，该地区准备在这些村庄之间建立 K 条新的道路，每条新道路可以连接任意两个村庄。

两条新道路可以在同一个村庄会合或结束，甚至新道路可以是一个环。

因为资金有限，所以 K 只能为1或2。

同时，为了不浪费资金，每天巡警车必须经过新建的道路正好一次。

编写一个程序，在给定村庄间道路信息和需要新建的道路数的情况下，计算出最佳的新建道路的方案，使得总的巡逻距离最小。

输入格式

第一行包含两个整数 n 和 K。

接下来 n-1 行每行两个整数 a 和 b，表示村庄 a 和 b 之间有一条道路。

输出格式

输出一个整数，表示新建了 K 条道路后能达到的最小巡逻距离。

数据范围

$3 \le n \le 100000$,
$1 \le K \le 2$,
$1 \le a,b \le n$

输入样例：

8 1
1 2
3 1
3 4
5 3
7 5
8 5
5 6

输出样例：

11

解题报告

题意理解

有一颗$n-1$个节点的树,警察局设在根节点,两个节点之间的距离固定是$1$,现在要求所有的节点都要至少访问一遍,可以访问多次.

猪八戒警察是个不愿意浪费多余时间的人死胖子,时间要花在睡觉吃饭上面,所以他只想要走最短的路.为什么胖,就是因为懒,贪吃

要致富先修路,于是上面派发了巨款修路,这笔巨款,居然可以添加一条路,或者两条路.巨款好多啊,全被猪八戒买东西吃掉了

不过有要求,那就是新修建的路,只准走一次,因为豆腐渣工程,不安全.

解题思路

题目分析

一道题目中,条件性质都是一座座宝藏,必须深入挖掘.才能成为yxc老师一般的人生赢家

1. 题目的核心是什么?

偷懒走最少的路

1. 换句话表示是什么?

不要走最长的路

1. 什么是最长的路?

树的直径

1. 树的直径是什么?

一棵树上,最远的两个点,他们的距离.

1. 添加路径有什么效果?

使得两个点的最短距离变成$1$.

1. 当只能增加一条新的路径的时候,我们怎么最大化利润?

找到树的直径的两个端点,在他们中间添加一条新路径.

样例分析

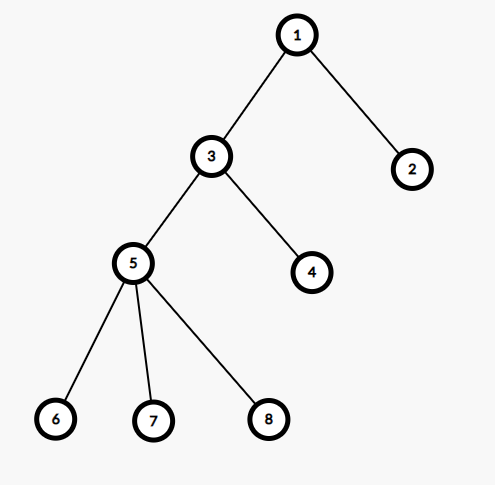
这是我们样例1的模型.

让我们来求一下这棵树的树的直径

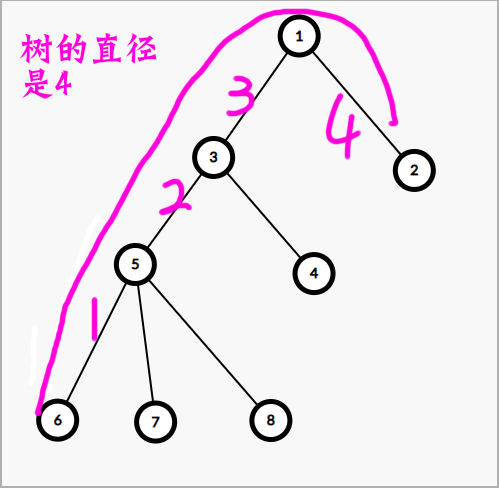
假如说我们将这条直径的两个端点相连接的话,我们最多可以优惠多少路径长度呢?

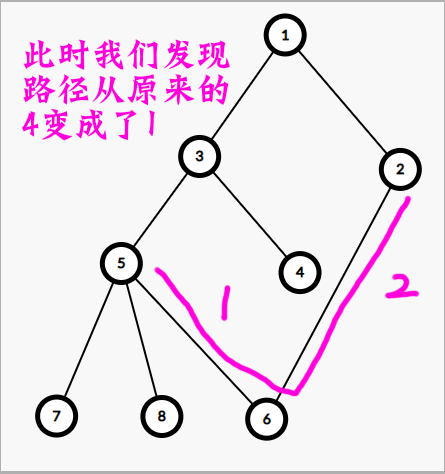
性质是什么,就是从一个特殊例子,变化成为一个通解公式

性质总结

因此我们通过上面的每一步,得到了如下的这些重要性质.

1. 刚开始我们一共要走的长度是:

$$ 路径总长度=2*(n-1)\\\\ n是这棵树上的节点个数 $$

因为对于每一个点而言,我们必须要走两次. (你可以认为就像是DFS搜索一样)

第一次访问这个点,也就是进入这个点.

第二次访问这个点,也就是离开这个点.

1. 假如说我们之前的树,它的树的直径长度是$L$,那么经过我们第一轮路径增加过后.

$$ 路径总长度-L+1 \\\\ 也就是2*(n-1)-L+1 $$

因为我们不必再走一遍树的直径了,所以我们减少了$L$的长度.

但是我们增加了一条边,所以我们增加了$1$的长度.

总而言之,言而总之,这就是我们对于增加一条边的性质总结.

重点思考

这道题目,不仅仅要让我们增加一条边,还有增加第二条边的可能.

假如说我们没有第一条边的建立,那么现在我们增加第二条边,其实所有步骤都是和上面建立第一条边是一样的.

1. 第一条边建立后的影响

我们知道,树之所以是树,是因为它不会出现环.

但是现在一条边的建立,环它出现了.是他,是他,就是他,我们的小英雄一组环

因为出现了环,所以我们现在不能保证一个点,那就是

第二条边构造的B环会不会和第一条边构造的A环,有重叠部分.

1. 假如说没有重叠部分

如果说没有重叠,那么第一条边和第二条边各自为政,井水不犯河水,我们可以看作是两次第一条边.

只需要把第一次步骤,重复两遍即可.

1. 如果有重叠部分

我们现在要明确一点,为什么我们添加边,可以使得路径缩小?

因为对于树的直径上的所有点,我们只需要进入一次,并不需要再离开一次了.

1. 但是重叠部分会导致什么呢?

对于一个节点而言,它是重叠部分上的点.

第一次,它被减少掉了一条边.

第二次,它再次被减少了一条边.

请问它还会被访问吗?

答案是不可能!因为我们一个节点,最多访问两次,而你减少了两次.

所以此时,我们的这些重叠部分上的点,从只需要访问一次,变成了需要访问两次.

因为我们必须去访问这些点,而访问了一次,又必须再离开一次,于是就是访问两次

算法流程

1. 在最初的树上,求出树的直径$L1$,然后将这条路径上的所有边权统统取反.
   $$ 1变成-1 $$

2. 我们再求一次树的直径$L2$.

3. 答案就是
   $$ 2 \times (n-1)-(L1-1)-(L2-1) \\\\ = 2 \times (n-1)-L1+1-L2+1 $$

假如说$L2$和$L1$有重叠部分.

那么当我们
$$ -L1+1 $$
的时候,我们就会发现,重叠的部分变成了只需要经过一次.

然后
$$ -L2+1 $$
相当于把重叠部分相加回来了.

此时变成了经过了两次.

假如说没有重叠部分,那么1,-1都不会有影响,反正我们不会经过这些边.

代码解析

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+20;
int n,k;
struct Edge
{
    int ver[2*N],edge[2*N],Next[2*N],head[N],dis[N],pre[N],f[N],v[N],tot,p,i,x,y,z;
    queue<int> q;
    void init()
    {
        memset(head,0,sizeof(head));
        tot=1;
    }
    void add_edge(int a,int b,int c)
    {
        edge[++tot]=b;
        ver[tot]=c;
        Next[tot]=head[a];
        head[a]=tot;
    }
    int bfs(int s)
    {
        int i,x,y;
        memset(dis,0x3f,sizeof(dis));
        q.push(s);
        dis[s]=pre[s]=0;
        while(q.size())
        {
            x=q.front();
            q.pop();
            for(i=head[x]; i; i=Next[i])
                if(dis[edge[i]]==0x3f3f3f3f)
                    dis[edge[i]]=dis[x]+ver[i],pre[edge[i]]=i,q.push(edge[i]);
        }
        for(x=y=1; x<=n; x++)
            if(dis[x]>dis[y])
                y=x;
        return y;
    }
    int diam()
    {
        p=bfs(1);
        p=bfs(p);
        return dis[p];
    }
    void change()
    {
        for(; pre[p]; p=edge[pre[p]^1]) ver[pre[p]]=ver[pre[p]^1]=-1;
    }
    void dp(int x)
    {
        v[x]=1;
        for(int i=head[x]; i; i=Next[i])
            if(!v[edge[i]])
            {
                dp(edge[i]);
                y=max(y,f[edge[i]]+f[x]+ver[i]);
                f[x]=max(f[x],f[edge[i]]+ver[i]);
            }
    }
    void work()
    {
        x=diam(),y=0,z=1;
        if(k==2)
            change(),dp(1),z=2;
        printf("%d\n",2*(n-1)-x-y+z);
    }
} g1;
int main()
{
//  freopen("stdin.in","r",stdin);
    scanf("%d%d",&n,&k);
    g1.init();
    for(int i=1; i<n; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        g1.add_edge(a,b,1);
        g1.add_edge(b,a,1);
    }
    g1.work();
    return 0;
}